Theoretische Informatik
Lindenmayer-Systeme
Ein Lindenmayer-System oder L-System (nach A. Lindenmayer
) ist, ähnlich wie eine Grammatik, ein Ersetzungssystem zur Beschreibung einer formalen Sprache. Im Unterschied zur Grammatik werden in einem L-System alle anwendbaren Ersetzungsregeln parallel ausgeführt.
Konzept
Definition: Ein deterministisches 0L-System (D0L-System) 1) ist ein Tripel
D = (A, P, s).
Hierbei ist
Die Produktionen eines D0L-Systems ordnen also jedem Zeichen des Alphabets ein Wort zu. Ähnlich wie bei einer Grammatik werden die Produktionen als Ersetzungsregeln aufgefasst: Jedes Zeichen a ∈ A lässt sich durch das Wort P(a) = w ersetzen; wir schreiben daher auch a → w.
Schreibweise: Bei D0L-Systemen geben wir Produktionen der Form a → a nicht explizit an. Wenn also für ein Alphabetzeichen a keine Produktion angeben ist, so gilt a → a.
Die Abbildung P lässt sich in natürlicher Weise auf ganze Wörter erweitern. Sie wird dadurch zu einem Halbgruppen-Homomorphismus P : A* → A*.
Definition: Sei x = x0 ... xn-1 ein Wort über A. Die Erweiterung der Abbildung P auf das Wort x ergibt sich als
P(x0 ... xn-1) = P(x0) ... P(xn-1)
Die Produktionen werden also auf alle Zeichen des Wortes x parallel angewandt. Aus dem Wort x entsteht so ein neues Wort P(x) = y; wir schreiben in diesem Fall auch x → y.
Auf das neue Wort y kann nun wieder P angewandt werden, usw. Auf diese Weise werden fortgesetzt neue Wörter erzeugt. Die Menge aller dieser Wörter bildet die von dem D0L-System erzeugte Sprache.
Definition: Sei D = (A, P, s) ein D0L-System. Die von D erzeugte Sprache ist
L(D) = { w | s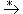 
w },
also die Menge aller Wörter, die durch parallele Anwendung der Produktionen in 0, einem oder mehreren Schritten aus dem Startwort erzeugt werden können. Ein solcher Schritt wird auch als Generation bezeichnet.
Der Unterschied zwischen einem D0L-System und einer kontextfreien Grammatik besteht zum einen darin, dass bei einem D0L-System in einem Ableitungsschritt alle anwendbaren Produktionen parallel angewendet werden, während bei einer Grammatik in einem Ableitungsschritt immer nur eine Produktion angewendet wird. Zum anderen wird bei einem D0L-System anders als bei einer Grammatik nicht zwischen Variablen und Terminalzeichen unterschieden.
Beispiele
Beispiel:
- Das D0L-System
D = ( {a}, {a → aa}, a )
erzeugt die Sprache
L(D) = { a2n | n ∈ ℕ0 } = { a, aa, aaaa, aaaaaaaa, ... }.
Die Längen der Wörter entsprechen den Zweierpotenzen.
Im ersten Ableitungsschritt wird das Zeichen a im Startwort gemäß der Produktion a → aa durch aa ersetzt. Im zweiten Ableitungsschritt werden in dem Wort aa alle vorkommenden a's parallel durch aa ersetzt, das Ergebnis ist aaaa, usw.
- Das D0L-System
D = ( {a, b}, {a → b, b → ab }, a )
erzeugt die Sprache
L(D) = { a, b, ab, bab, abbab, bababbab, ... }.
Ab dem dritten Wort ergibt sich jedes Wort als Verkettung der beiden vorherigen Wörter. Die Längen der Wörter entsprechen den Fibonacci-Zahlen.
In folgendem Beispiel ist gemäß der oben vereinbarten Schreibweise die Produktion c → c nicht explizit angegeben:
- Das D0L-System
D = ( {a, b, c}, {a → abcc, b → bcc }, a )
erzeugt die Sprache
L(D) = { a, abcc, abccbcccc, abccbccccbcccccc, ... }.
Die Längen der Wörter entsprechen den Quadratzahlen.
Die Beispiele zeigen zunächst, dass mit L-Systemen unterschiedliche Wachstumsfunktionen realisiert werden können. In der Praxis werden L-Systeme vorwiegend zur Erzeugung von geometrischen Objekten verwendet. Hierbei werden die Alphabetzeichen als bestimmte geometrische Operationen interpretiert.
Literatur
[Sal 73] A.K. Salomaa: Formal Languages. Academic Press (1973)
1) In der Bezeichnung 0L-System steht die 0 (Null) für kontextfrei (Null Kontext). Die Aussprache ist aber "Oh-El-System".
Weiter mit: [Raumfüllende Kurven] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 20.12.2012 Updated: 21.03.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden