Theoretische Informatik
Grammatik
Eine endliche Sprache lässt sich einfach durch Aufzählung aller ihrer Wörter angeben. Um eine unendliche Sprache angeben zu können, benötigt man eine endliche Beschreibung der Sprache. Eine solche existiert nur, wenn alle Wörter der Sprache einem bestimmten Bildungsgesetz folgen (z.B. "alle Wörter, die mit a anfangen, mindestens fünf b's und genauso viele c's enthalten und mit a oder c aufhören"). Es gibt Sprachen, die keine endliche Beschreibung haben, denn es gibt überabzählbar viele Sprachen, aber nur abzählbar viele endliche Beschreibungen.
In der Theorie der formalen Sprachen werden Grammatiken zur Beschreibung von Sprachen verwendet. Mithilfe einer Grammatik lassen sich die Wörter einer Sprache L erzeugen: Ein Wort gehört zu L, wenn es sich durch eine Folge von bestimmten zulässigen Ersetzungen aus einem sogenannten Startsymbol erzeugen lässt.
Grammatik
Definition: Eine Grammatik ist ein 4-Tupel
G = (V, T, P, S).
Hierbei ist
| V | das Alphabet der Variablen oder Nicht-Terminalzeichen, | |
| T | das Alphabet der Terminalzeichen, | |
| hierbei gilt: V ∩ T = ∅; ferner sei A = V ∪ T das Gesamtalphabet, | ||
| P ⊆ A+ × A* | eine endliche Relation; die Elemente von P heißen Produktionen oder Ersetzungsregeln, | |
| S ∈ V | eine spezielle Variable, das Startsymbol. |
Durch die Produktionen oder Ersetzungsregeln wird festgelegt, wie aus Wörtern w über dem Gesamtalphabet A neue Wörter gebildet werden können. Eine Produktion wird auf ein Wort w angewendet, indem in w nach einem Vorkommen der linken Seite der Produktion gesucht wird und dieses Vorkommen durch die rechte Seite der Produktion ersetzt wird. Das Ergebnis ist ein Wort w'.
Beispiel: Seien (S, ab) und (S, aSb) Produktionen und sei w = S. Indem in w die zweite Produktion auf S angewendet wird, ergibt sich als Ergebnis w' = aSb. Indem in w' = aSb die erste Produktion auf S angewendet wird, ergibt sich w'' = aabb.
Ableitung von Wörtern
Die Anwendung einer Produktion auf ein Wort w wird als Ableitungsschritt bezeichnet. Wie im Beispiel angedeutet, können mehrere Ableitungsschritte aufeinander folgen. Eine solche Folge von Ableitungsschritten wird als Ableitungsfolge bezeichnet.
Die Menge aller Paare (w, w') von Wörtern, bei denen sich w' durch Anwendung einer Produktion, also durch einen Ableitungsschritt aus w erzeugen lässt, bildet eine Relation → auf A+ × A*.
Definition: Sei G = (V, T, P, S) eine Grammatik und sei A = V ∪ T. Die Relation P lässt sich in natürlicher Weise zu einer Relation → ⊆ A+ × A* erweitern, indem für alle w, w' ∈ A+ definiert wird:
w → w' ⇔ ∃ x, y ∈ A*, (u, v) ∈ P : w = xuy ∧ w' = xvy
Es gilt also w → w', wenn innerhalb des Wortes w ein Vorkommen der linken Seite u einer Produktion (u, v) durch die zugehörige rechte Seite v ersetzt wird und das Ergebnis das Wort w' ist.
Offensichtlich gilt auch u → v für alle Produktionen (u, v) ∈ P. Wir schreiben deshalb Produktionen auch in der Form u → v.
Die Sprechweise für die Relation → ist wie folgt: Das Wort w erzeugt direkt das Wort w' oder w' lässt sich aus w direkt ableiten oder w' ist direkt ableitbar aus w.
Die reflexive und transitive Hülle von → ist die Relation 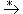 . Es gilt w
. Es gilt w 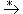 w', wenn w' durch eine Ableitungsfolge, d.h. in 0 oder mehr Ableitungsschritten, aus w ableitbar ist, (Sprechweise: w' ist ableitbar aus w oder w erzeugt w').
w', wenn w' durch eine Ableitungsfolge, d.h. in 0 oder mehr Ableitungsschritten, aus w ableitbar ist, (Sprechweise: w' ist ableitbar aus w oder w erzeugt w').
Erzeugung einer Sprache
Definition: Die von einer Grammatik G = (V, T, P, S) erzeugte Sprache L(G) ist die Menge aller nur aus Terminalzeichen bestehenden Wörter, die aus dem Startsymbol S ableitbar sind:
L(G) = { w ∈ T* | S 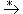 w }
w }
Das folgende Beispiel veranschaulicht, wie ein Wort einer Sprache aus dem Startsymbol der Grammatik abgeleitet wird.
Beispiel: Gegeben sei folgende Grammatik G = (V, T, P, S) mit
V = {S}, T = {a, b}, P = { S → aSb, S → ab }
Aus dem Startsymbol S lässt sich beispielsweise aSb direkt ableiten; aus aSb lässt sich aaSbb direkt ableiten; aus aaSbb lässt sich aaabbb direkt ableiten (durch Anwendung der Produktion S → ab).
Die Folge
| S | |
| → | aSb |
| → | aaSbb |
| → | aaabbb |
ist die Ableitungsfolge für aaabbb.
Die von G erzeugte Sprache ist
L(G) = { anbn | n ∈ ℕ } = { ab, aabb, aaabbb, ... }
Im Folgenden fassen wir Produktionen mit gleicher linker Seite zu einer Produktion mit verschiedenen Alternativen als rechter Seite zusammen. Die beiden Produktionen aus dem vorigen Beispiel ergeben damit die Produktion
| S |  | aSb | ab |
Weitere Beispiele
Es folgen zwei weitere Beispiele für Grammatiken.
Beispiel: Gegeben sei folgende Grammatik G = (V, T, P, S) mit
V = {S, X, Y}, T = {a, b}
und den Produktionen
| S |  | XSY | ε |
| XY |  | YX |
| X |  | a |
| Y |  | b |
Die Grammatik erzeugt die Sprache
L(G) = { w ∈ {a, b}* | |w|a = |w|b }
bestehend aus allen Wörtern, die gleich viele a's und b's enthalten.
Beispiel: Gegeben sei folgende Grammatik G = (V, T, P, S) mit
V = {S}, T = {a, b}
und den Produktionen
| S |  | aSa | bSb | ε |
Die Grammatik erzeugt die Sprache
L(G) = { wwR | w ∈ {a, b}*, wR ist das Spiegelbild von w }
der Palindrome1) gerader Länge über dem Alphabet {a, b}.
Aufgaben
Aufgabe 1: Geben Sie jeweils eine Ableitungsfolge für das Wort abba in den Grammatiken aus dem vorigen Abschnitt an.
Aufgabe 2: Entwerfen Sie eine Grammatik G = (V, T, P, S) für die Sprache
L = { w ∈ {a, b}* | w = wR }
aller Palindrome (gerader und ungerader Länge) über dem Alphabet {a, b}.
Aufgabe 3: Entwerfen Sie eine Grammatik G = (V, T, P, S) für die Sprache
L = A*
aller Wörter über dem Alphabet A = {a, b}.
Aufgabe 4: Beschreiben Sie informell mit Worten, welche Sprache durch eine Grammatik mit folgenden Produktionen erzeugt wird.
| S |  | aX | a |
| X |  | aX | bX | a |
Aufgabe 5:
Die Grammatik mit den Produktionen
S aSbS | ε
aSbS | ε
erzeugt die Sprache L(G) = { w | w stellt eine korrekt aufgebaute Klammerstruktur dar, wobei a einer öffnenden und b einer schließenden Klammer entspricht }
Geben Sie eine Ableitungsfolge für das Wort w = aababbab an.
Zusammenfassung
Mithilfe einer Grammatik und ihrer Produktionen lassen sich aus dem Startsymbol durch eine Folge von Ersetzungen Wörter erzeugen. Alle Wörter, die sich aus dem Startsymbol erzeugen lassen und die nur aus Terminalzeichen bestehen, bilden die von der Grammatik erzeugte Sprache.
1) Ein Palindrom ist ein Wort, das man vorwärts und rückwärts lesen kann, wie z.B. otto.
Weiter mit: [Chomsky-Hierarchie der Grammatiktypen] [Kontextfreie Grammatik] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 26.01.2003 Updated: 16.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden