Theoretische Informatik
Lindenmayer-Systeme: Raumfüllende Kurven
Ein interessantes Anwendungsgebiet von L-Systemen ist die Erzeugung von selbstähnlichen geometrischen Objekten. Selbstähnlich bedeutet hier, dass das Objekt in ähnlicher Form Teil seiner selbst ist.
Hierzu werden die Alphabetzeichen des L-Systems als geometrische Operationen oder Objekte interpretiert. Jedes Vorkommen eines Alphabetzeichens im erzeugten Wort des L-Systems entspricht einer geometrischen Operation oder einem geometrischen Objekt in einer bestimmten Lage im Raum.
Als erstes betrachten wir die Erzeugung von raumfüllenden Kurven; dies sind Linien, die eine Fläche oder einen Raum beliebig dicht ausfüllen.
Turtle-Grafik
Eine Möglichkeit der geometrischen Interpretation der Alphabetzeichen sind sogenannte Turtle-Grafik-Operationen. Die Vorstellung ist hier, dass ein Roboter auf der Zeichenebene hin- und herfährt und dabei Linien zeichnet 1). Er wird durch die folgenden vier einfachen Kommandos gesteuert:
| F(x) | Vorwärtsbewegung um eine bestimmte Länge x und dabei zeichnen | |
| f(x) | Vorwärtsbewegung um eine bestimmte Länge x, ohne zu zeichnen | |
| +(α) | Richtungsänderung nach links um einen bestimmten Winkel α | |
| –(α) | Richtungsänderung nach rechts um einen bestimmten Winkel α |
Im Folgenden ordnen wir zunächst den Alphabetzeichen F, + und – die geometrischen Operationen F(1), +(90°) und –(90°) zu. Somit beschreibt beispielsweise das Wort F+F+F+F ein Quadrat der Kantenlänge 1.
Hilbert-Kurve
Eine Hilbert-Kurve (nach D. Hilbert
) ist eine Linie, die eine Fläche beliebig dicht ausfüllt, je nach Anzahl der Iterationen. Wir beschreiben im Folgenden eine Hilbert-Kurve durch ein L-System, dessen Zeichen als Turtle-Grafik-Operationen interpretiert werden.
Das D0L-System D = (A, P, s) mit
| A | = | { X, Y, F, +, – } |
| P | : | X → +YF–XFX–FY+ |
| Y → –XF+YFY+FX– | ||
| s | = | X |
erzeugt Hilbert-Kurven. Hierbei entsprechen die Zeichen F, + und – den Turtle-Grafik-Operationen Vorwärtsbewegung mit Zeichnen, Linkswendung und Rechtswendung. Die Zeichen X und Y haben keine geometrische Interpretation, sie steuern den Ersetzungsvorgang an den Ecken der Kurve.
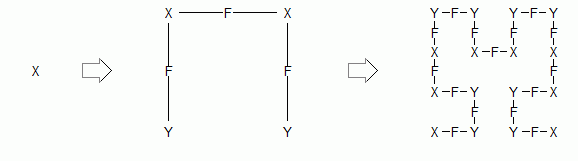
Bild 1: Erste und zweite Generation des L-Systems und zugehörige Hilbert-Kurven
Visualisierung Hilbert-Kurve
Die folgende Visualisierung zeigt die Ergebnisse der ersten sechs Generationen des L-Systems, interpretiert als Hilbert-Kurven.
Nächste Generation:
Peano-Kurve
Eine andere raumfüllende Kurve ist die Peano-Kurve (nach G. Peano).
Das D0L-System D = (A, P, s) mit
| A | = | { X, Y, F, +, – } |
| P | : | X → XFYFX–F–YFXFY+F+XFYFX |
| Y → YFXFY+F+XFYFX–F–YFXFY | ||
| s | = | X |
erzeugt eine Peano-Kurve. Wiederum entsprechen die Zeichen F, + und – den Turtle-Grafik-Operationen Vorwärtsbewegung mit Zeichnen, Linkswendung und Rechtswendung, und die Zeichen X und Y haben keine geometrische Interpretation, sie steuern den Ersetzungsvorgang.
Visualisierung
Die folgende Visualisierung zeigt die Ergebnisse der ersten vier Generationen des L-Systems, interpretiert als Peano-Kurven.
Nächste Generation:
Literatur
[Sal 73] A.K. Salomaa: Formal Languages. Academic Press (1973)
1) Als es noch keine Roboter gab, nahm man eine Schildkröte (engl.: turtle), die man mithilfe eines Salatblatts in die gewünschte Richtung lockte.
Weiter mit: [Fraktale] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 20.12.2012 Updated: 21.03.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden