Theoretische Informatik
Chomsky-Hierarchie der Automatentypen
Der Chomsky-Hierarchie der Grammatiktypen entspricht eine Hierarchie der Automatentypen. Dies sind die Automatentypen Turingmaschine, linear beschränkte Turingmaschine, Stackautomat und endlicher Automat. Ziel ist es hier, diese Automatentypen als echte Spezialfälle voneinander darzustellen. Dazu ist es erforderlich, die entsprechenden Automatentypen ein wenig zu modifizieren. Denn ein Stackautomat mit seinen zwei Bändern, dem Eingabeband und dem Stack, kann kein Spezialfall einer Ein-Band-Turingmaschine sein. Die Hierarchie beginnt daher mit einer speziellen Zwei-Band-Turingmaschine.
Typ-i-Automaten
Wir bezeichnen die entsprechend modifizierten Automatentypen als Typ-i-Automaten. Die Modifikationen sind notwendig, damit eine echte Hierarchie von Spezialfällen zustande kommt.
Typ 0
Ein Typ-0-Automat ist eine nichtdeterministische Zwei-Band-Turingmaschine mit einem Eingabeband und einem einseitig unbeschränkten Arbeitsband. Auf dem Eingabeband steht das Eingabewort. Die Turingmaschine kann auf dem Eingabeband nur von links nach rechts lesen. Auf dem Arbeitsband kann sie lesen und schreiben und sich beliebig nach links und rechts bewegen, jedoch nicht über das linke Begrenzungszeichen $ hinaus. Das Begrenzungszeichen darf sie nicht durch ein anderes Zeichen überschreiben.
Das folgende Bild 1 zeigt schematisch einen Typ-0-Automaten mit Eingabewort x = x0 ... x5 auf dem Eingabeband.
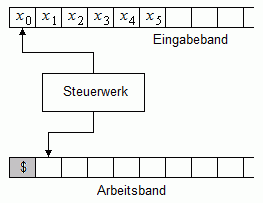
Bild 1: Typ-0-Automat mit Eingabeband und Arbeitsband
Formal ist ein Typ-0-Automat wie folgt definiert:
Definition: Ein Typ-0-Automat ist ein Tupel
M = (Z, E, A, d, q, F).
Hierbei ist
| Z | eine endliche, nichtleere Menge von Zuständen des Steuerwerks, | |
| E | das Eingabealphabet, ferner E' = E ∪ { }, }, | |
| A | das Arbeitsalphabet, wobei E' ⊆ A, | |
| d | die Übergangsrelation mit d ⊆ Z × E'? × A × A' × Z, | |
| hierbei ist A' = A ∪ {L, R} sowie E'? = E' ∪ {ε}, | ||
| q ∈ Z | der Startzustand, | |
| F ⊆ Z | die Menge der Endzustände. |
Das Leerzeichen  steht für ein leeres Feld auf dem Eingabe- bzw. dem Arbeitsband; es kommt nicht im Eingabealphabet vor. Das Arbeitsalphabet enthält ferner das Bandbegrenzungszeichen $; dieses kommt ebenfalls nicht im Eingabealphabet vor. Die Zeichen L und R bedeuten eine Links- bzw. eine Rechtsbewegung des Schreib-/Lesekopfes auf dem Arbeitsband; diese Zeichen kommen nicht im Arbeitsalphabet vor.
steht für ein leeres Feld auf dem Eingabe- bzw. dem Arbeitsband; es kommt nicht im Eingabealphabet vor. Das Arbeitsalphabet enthält ferner das Bandbegrenzungszeichen $; dieses kommt ebenfalls nicht im Eingabealphabet vor. Die Zeichen L und R bedeuten eine Links- bzw. eine Rechtsbewegung des Schreib-/Lesekopfes auf dem Arbeitsband; diese Zeichen kommen nicht im Arbeitsalphabet vor.
Ein Tupel (s, a, h, h', s') der Übergangsrelation bewirkt folgende Aktion des Automaten: Wenn sich der Automat im Zustand s befindet und das Zeichen a auf dem Eingabeband und das Zeichen h auf dem Arbeitsband liest, so schreibt er das Zeichen h' auf das Arbeitsband und geht in den Zustand s' über. Wenn allerdings h' eines der Zeichen L oder R ist, so schreibt der Automat kein Zeichen, sondern führt stattdessen eine Links- bzw. Rechtsbewegung des Schreib-/Lesekopfes auf dem Arbeitsband aus. Nach dem Lesen eines Zeichens a auf dem Eingabeband führt der Automat eine Rechtsbewegung des Lesekopfes auf dem Eingabeband aus, nicht jedoch wenn a = ε ist.
Zu Beginn steht der Lesekopf auf dem ersten Feld des Eingabebandes und der Schreib-/Lesekopf auf dem Feld neben dem Bandbegrenzungszeichen des Arbeitsbandes.
Der Automat hält, wenn er keinen Zustandsübergang mehr ausführen kann. Der Automat erkennt das Wort auf dem Eingabeband, wenn er hält und sich dabei in einem Endzustand befindet.
Beispiel: Der folgende Typ-0-Automat M = (Z, E, A, d, q, F) erkennt die Sprache L = { anbncn | n ∈ ℕ }.
Es ist Z = {0, ..., 7}, E = {a, b, c}, A = {a, b, c, x,  , $}, q = 0, F = {7}; die Übergangsrelation d ist
, $}, q = 0, F = {7}; die Übergangsrelation d ist
Bemerkung: Zwei-Band-Turingmaschinen und normale Turingmaschinen sind äquivalente Maschinenmodelle. Zwei-Band-Turingmaschinen lassen sich durch normale Turingmaschinen simulieren und umgekehrt.
Typ 1
Definition: Ein Typ-1-Automat ist ein Typ-0-Automat, dessen Übergangsrelation wie folgt eingeschränkt ist:
Jeder Zustandsübergang, der das Leerzeichen  auf dem Arbeitsband vorfindet, überschreibt dieses durch ein Zeichen und liest gleichzeitig ein Eingabezeichen ein oder aber führt eine Linksbewegung aus.
auf dem Arbeitsband vorfindet, überschreibt dieses durch ein Zeichen und liest gleichzeitig ein Eingabezeichen ein oder aber führt eine Linksbewegung aus.
Ein Typ-1-Automat darf also ein Leerzeichen auf dem Arbeitsband nur dann überschreiben, wenn er gleichzeitig ein Eingabezeichen liest. Eine Rechtsbewegung darf er bei einem Leerzeichen auf dem Arbeitsband gar nicht ausführen.
Erreicht wird hierdurch, dass der Typ-1-Automat höchstens so viele Felder des Arbeitsbandes benutzt wie Eingabezeichen auf dem Eingabeband stehen. Ein Typ-1-Automat benutzt also nur einen durch die Länge der Eingabe beschränkten Teil des Arbeitsbandes.
Bei einem Typ-1-Automaten sind also Zustandsübergänge der Form (s, ε,  , x, s') mit x ∈ A verboten. Erlaubt ist dagegen (s, a,
, x, s') mit x ∈ A verboten. Erlaubt ist dagegen (s, a,  , x, s') mit a ∈ E', x ∈ A, ebenso (s, ε,
, x, s') mit a ∈ E', x ∈ A, ebenso (s, ε,  , L, s').
, L, s').
Beispiel: Der Typ-0-Automat aus dem vorigen Beispiel ist ein Typ-1-Automat.
Bemerkung: Typ-1-Automaten sind äquivalent zu den klassischen linear beschränkten Turingmaschinen.
Typ 2
Ein Typ-2-Automat benutzt sein Arbeitsband in noch weiter eingeschränkter Weise, nämlich wie einen Stack. Ob ein Automat vom Typ 2 ist, lässt sich nicht an den einzelnen Zustandsübergängen ablesen, sondern nur indem zu gewissen Zustandsübergängen auch die möglichen Folge-Zustandsübergänge berücksichtigt werden.
Definition: Ein Typ-2-Automat ist ein Typ-1-Automat, dessen Übergangsrelation wie folgt eingeschränkt ist:
- Wenn (s, a,
 , x, t) mit x ∈ A ein Zustandsübergang ist, dann gilt für alle Folge-Zustandsübergänge (t, a', x, h', s'), dass h' = R ist, d.h. nach dem Überschreiben eines Leerzeichens findet eine Rechtsbewegung statt.
, x, t) mit x ∈ A ein Zustandsübergang ist, dann gilt für alle Folge-Zustandsübergänge (t, a', x, h', s'), dass h' = R ist, d.h. nach dem Überschreiben eines Leerzeichens findet eine Rechtsbewegung statt.
- Wenn (s, a,
 , L, t) ein Zustandsübergang ist, dann gilt für alle Folge-Zustandsübergänge (t, a', h, h', s'), dass h' =
, L, t) ein Zustandsübergang ist, dann gilt für alle Folge-Zustandsübergänge (t, a', h, h', s'), dass h' =  oder h' = R ist, d.h. nach einer Linksbewegung wird ein Leerzeichen geschrieben oder eine Rechtsbewegung ausgeführt.
oder h' = R ist, d.h. nach einer Linksbewegung wird ein Leerzeichen geschrieben oder eine Rechtsbewegung ausgeführt.
Ein Typ-2-Automat ist ein Spezialfall eines Typ-1-Automaten.
Beispiel: Folgender Automat M = (Z, E, A, d, q, F) erkennt die Sprache L = { anbn | n ∈ ℕ }.
Es ist Z = {0, ..., 5}, E = {a, b}, A = {a, b,  , $}, q = 0, F = {5}; die Übergangsrelation d ist
, $}, q = 0, F = {5}; die Übergangsrelation d ist
Anhand der Übergangsrelation ist ersichtlich, dass es sich hier um einen Typ-2-Automaten handelt. Beispielsweise wird durch den Zustandsübergang (1, a,  , a, 2) ein Leerzeichen auf dem Arbeitsband überschrieben. Daher müssen alle Folge-Zustandsübergänge eine Rechtsbewegung ausführen. Der einzige Folge-Zustandsübergang, der vom Zustand 2 ausgeht, führt tatsächlich eine Rechtsbewegung aus.
, a, 2) ein Leerzeichen auf dem Arbeitsband überschrieben. Daher müssen alle Folge-Zustandsübergänge eine Rechtsbewegung ausführen. Der einzige Folge-Zustandsübergang, der vom Zustand 2 ausgeht, führt tatsächlich eine Rechtsbewegung aus.
In ähnlicher Weise lässt sich überprüfen, dass die Bedingung für Linksbewegungen hier ebenfalls erfüllt ist.
Bemerkung: Offenbar ist ein Typ-2-Automat äquivalent zu einem klassischen Stackautomaten, allerdings mit beschränkter Länge des Stacks. Für die Erkennung von Sprachen ist diese Beschränkung aber ohne Belang.
Ein Überschreiben eines Leerzeichens auf dem Arbeitsband mit anschließender Rechtsbewegung entspricht der push-Operation des Stackautomaten, eine Linksbewegung mit anschließendem Überschreiben eines Zeichens durch das Leerzeichen entspricht der pop-Operation. Eine Linksbewegung mit anschließender Rechtsbewegung entspricht einer pop-Operation, in der ein Zeichen vom Stack entfernt wird, gefolgt von einer push-Operation, in der dasselbe Zeichen wieder auf dem Stack abgelegt wird.
Typ 3
Definition: Ein Typ-3-Automat ist ein Typ-2-Automat, bei dem alle Zustandsübergänge von der Form (s, a,  ,
,  , s') sind.
, s') sind.
Ein Typ-3-Automat benutzt sein Arbeitsband überhaupt nicht, sondern liest nur auf dem Eingabeband und vollführt dabei Zustandsübergänge.
Ein Typ-3-Automat ist ein Spezialfall eines Typ-2-Automaten.
Beispiel: Der folgende nichtdeterministische Typ-3-Automat M = (Z, E, A, d, q, F) erkennt die Sprache L = a | a(a|b)*a.
Es ist Z = {0, ..., 3}, E = {a, b}, A = {a, b,  , $}, q = 0, F = {3}; die Übergangsrelation d ist
, $}, q = 0, F = {3}; die Übergangsrelation d ist
Bemerkung: Offenbar ist ein Typ-3-Automat dasselbe wie ein klassischer endlicher Automat mit Epsilon-Übergängen, mit dem Unterschied, dass der Typ-3-Automat erst dann in den Endzustand übergeht, wenn er zum Schluss noch ein Leerzeichen auf dem Eingabeband liest und dadurch feststellt, dass er das Eingabewort vollständig gelesen hat.
Aufgaben
Zusammenfassung
Wir haben den Typ-0-Automaten als nichtdeterministische Zwei-Band-Turingmaschine mit Eingabeband und Arbeitsband eingeführt. Indem die Möglichkeiten, das Arbeitsband zu benutzen, immer weiter eingeschränkt werden, ergeben sich Typ-1-, Typ-2- und Typ-3-Automaten. Ein Typ-3-Automat benutzt sein Arbeitsband überhaupt nicht mehr. Etwas künstlich erscheint allerdings die Beschränkung der Möglichkeiten, das Arbeitsband zu benutzen, beim Typ-2-Automaten.
Es stellt sich heraus, dass diese Beschränkungen gerade so gefasst sind, dass die entsprechenden Typ-i-Automaten genau die Typ-i-Sprachen der Chomsky-Hierarchie erkennen.
Die Chomsky-Hierarchie lässt sich auch durch eine andere spezielle Art von Turingmaschinen, bezeichnet als String-Turingmaschinen, charakterisieren. Hier ergeben sich die entsprechenden Typ-i-String-Turingmaschinen durch sehr viel natürlichere Beschränkungen.
Weiter mit: [String-Turingmaschinen] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 27.08.2010 Updated: 16.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden