Theoretische Informatik
Stackautomat
Erkennung von kontextfreien Sprachen
Wir hatten gesehen, dass die regulären Sprachen genau von den (nichtdeterministischen oder deterministischen) endlichen Automaten erkannt werden. Die kontextfreien Sprachen werden genau von den nichtdeterministischen Stackautomaten erkannt.
Ein Stackautomat ist ein endlicher Automat, der zusätzlich mit einem Stack als Arbeitsspeicher ausgerüstet ist (Bild 1).
als Arbeitsspeicher ausgerüstet ist (Bild 1).
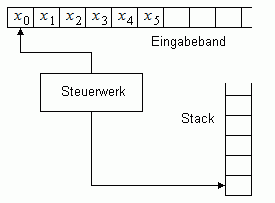
Bild 1: Prinzip des Stackautomaten
Zu Beginn der Verarbeitung steht ein Wort w am Anfang des Eingabebandes. Der Stack ist leer und der Automat befindet sich in seinem Startzustand.
In jedem Zustand kann der Stackautomat ein Zeichen des Eingabewortes lesen sowie das oberste Zeichen vom Stack lesen und entfernen, er kann ein Zeichen auf den Stack legen und einen Folgezustand annehmen.
Wenn es eine endliche Folge von solchen Zustandsübergängen gibt, in deren Verlauf der Stackautomat das Eingabewort w vollständig liest und am Ende einen Endzustand erreicht, so erkennt der Automat das Wort w.
Während der endliche Automat nur über einen endlichen Speicher, nämlich seine endlich vielen Zustände verfügt, ist der Stackautomat mit einem unbeschränkt großen Speicher ausgerüstet, nämlich dem Stack. Dies versetzt den Stackautomaten in die Lage, Sprachen zu erkennen, die ein endlicher Automat nicht erkennen kann.
Wir haben gesehen, dass die Sprache anbn nicht regulär ist; den Beweis haben wir mithilfe des Pumping Lemmas geführt. Es gibt also keinen endlichen Automaten, der diese Sprache erkennt. Der Grund besteht darin, dass ein endlicher Automat wegen seiner beschränkten Anzahl von Zuständen nicht beliebig weit zählen kann – er muss aber für beliebig großes n zählen, wieviele a's er gelesen hat, um anschließend zu prüfen, ob danach genauso viele b's kommen.
Für einen Stackautomaten ist die Erkennung der Sprache anbn kein Problem: Er legt jedes gelesene a auf den Stack und entfernt anschließend für jedes gelesene b ein a vom Stack. Wenn er das Eingabewort vollständig gelesen hat und den Stack wieder geleert hat, erkennt er das Wort. Das genaue Programm für diesen Stackautomaten folgt als nächstes Beispiel.
Definition
Definition: Ein nichtdeterministischer Stackautomat 1) ist ein Tupel
N = (Z, E, H, d, q, F).
Hierbei ist
| Z | eine endliche, nichtleere Menge von Zuständen, | |
| E | das Eingabealphabet, ferner sei E? = E ∪ {ε}, | |
| H | das Stackalphabet, ferner sei H? = H ∪ {ε}, | |
| d | die Übergangsrelation d ⊆ Z × E? × H? × H? × Z, | |
| q ∈ Z | der Startzustand, | |
| F ⊆ Z | die Menge der Endzustände. |
Die Übergangsrelation d ist sozusagen das Programm des Stackautomaten; sie wird in Form einer Tabelle dargestellt. Ein Element (s, e, h, h', s') der Übergangsrelation d hat folgende Bedeutung: Im Zustand s kann der Automat das Eingabezeichen e lesen, das Zeichen h vom Stack entfernen, das Zeichen h' auf den Stack legen und anschließend in den Zustand s' übergehen.
Ist e = ε, so vollführt der Automat einen Zustandsübergang, ohne ein Zeichen des Eingabewortes zu lesen. Er kann dabei ein Zeichen vom Stack entfernen, er kann auch ein Zeichen auf den Stack legen. Ist h = ε, so entfernt der Automat kein Zeichen vom Stack. Ist h' = ε, so legt der Automat kein Zeichen auf den Stack.
Deterministischer Stackautomat
Wenn in jeder Situation nur höchstens ein Zustandsübergang möglich ist, so ist der Stackautomat deterministisch. Ein deterministischer Stackautomat ist ein Spezialfall des nichtdeterministischen Stackautomaten, bei dem zunächst die Übergangsrelation eine partielle Funktion ist:
d : Z × E? × H? → H? × Z
Darüber hinaus darf im Definitionsbereich der Funktion nur jeweils eines der Tupel
(s, a, h)
(s, ε, h)
(s, a, ε)
(s, ε, ε)
vorkommen, für alle s ∈ Z, a ∈ E und h ∈ H.
Wenn beispielsweise die Tupel (1, a, ε) und (1, ε, ε) im Definitionsbereich der Übergangsfunktion vorkommen, kann der Automat im Zustand 1 das Zeichen a lesen oder nicht lesen; dies ist Nichtdeterminismus und bei einem deterministischen Stackautomaten nicht zulässig.
Erkennung von Wörtern
Definition: Ein Stackautomat erkennt ein Wort w, wenn es eine endliche Folge von Zustandsübergängen gibt, die das Eingabewort w vollständig abarbeitet und einen Endzustand erreicht.
Die von einem Stackautomat N erkannte Sprache L(N) ist die Menge aller Wörter, die der Stackautomat N erkennt.
Beispiel: Der folgende Stackautomat N = (Z, E, H, d, q, F) erkennt die Sprache { anbn | n ∈ ℕ }.
Z = {0, 1, 2, 3}
E = {a, b}
H = {$, a}
q = 0
F = {3}
d:
Der Stackautomat legt zunächst das Zeichen $ auf den Stack, um dessen unteres Ende zu kennzeichnen. Danach legt er solange jedes gelesene a auf den Stack, bis er auf das erste b stößt. Für jedes gelesene b entfernt er von nun an ein a vom Stack. Wenn er das Zeichen $ im Stack vorfindet, geht er in den Endzustand 3 über.
In dieser Situation ist kein weiterer Zustandsübergang mehr möglich. Falls das Eingabewort w nun vollständig gelesen ist, erkennt der Stackautomat das Wort w.
Dieser Stackautomat ist sogar deterministisch, denn es gibt in jeder Situation nur höchstens einen möglichen Zustandsübergang.
Nichtdeterministischer / deterministischer Stackautomat
Bei den endlichen Automaten ist es so, dass die deterministischen endlichen Automaten, obwohl sie nur einen Spezialfall der nichtdeterministischen endlichen Automaten darstellen, prinzipiell genauso viel können – beide erkennen genau die regulären Sprachen. Wir haben dies mithilfe der Teilmengenkonstruktion bewiesen.
Bei den Stackautomaten ist die Situation anders, die deterministischen Stackautomaten können weniger als die nichtdeterministischen. Es gibt Sprachen, die von einem nichtdeterministischen Stackautomaten erkannt werden, aber von keinem deterministischen Stackautomaten.
Ein Beispiel für eine solche Sprache ist die Sprache
{ wwR | w ∈ {a, b}+, wR ist das Spiegelbild von w }
über dem Alphabet A, also die Menge aller nichtleeren Wörter, die sich in w und w rückwärts gelesen zerlegen lassen.
Ein solches Wort ist z.B. otto, mit w = ot und wR = to. Andere Beispiele sind anna, retter oder reittier. Ein Wort, das vorwärts und rückwärts gelesen dasselbe ergibt, heißt Palindrom. Die Sprache wwR enthält allerdings nur die Palindome gerader Länge, also z.B. nicht uhu oder rentner.
Der folgende nichtdeterministische Stackautomat N = (Z, E, H, d, q, F) erkennt die Sprache aller Wörter der Form wwR über dem Alphabet {a, b}.
Z = {0, 1, 2, 3}
E = {a, b}
H = {$, a, b}
q = 0
F = {3}
d:
Der Stackautomat legt zunächst alle gelesenen Zeichen von w auf den Stack und entfernt diese anschließend korrespondierend zu den gelesenen spiegelbildlichen Zeichen von wR wieder vom Stack. An der Grenze zwischen w und wR schaltet der Stackautomat von "Ablegen auf dem Stack" zu "Entfernen vom Stack" um. Dies kann nur nichtdeterministisch geschehen. Ein deterministischer Stackautomat weiß nicht, wo w endet und wR beginnt.
Erkennen durch leeren Stack
Typischerweise erkennt ein Stackautomat ein Wort w dann, wenn er es vollständig gelesen hat und wenn dann der Stack wieder leer ist. In den Beispielen war dies der Fall; wir haben allerdings ein zusätzliches Zeichen $ benötigt, um das untere Ende des Stacks zu kennzeichnen und dadurch festzustellen, ob der Stack – bis auf dieses Zeichen – leer ist.
Häufig wird daher der Einfachheit halber eine Variante des Stackautomaten verwendet, der keine Endzustände hat, sondern ein Wort w dadurch erkennt, dass der Stack leer ist, nachdem er das Wort verarbeitet hat 2).
Es lässt sich zeigen, dass bei nichtdeterministischen Stackautomaten diese beiden Varianten, die mit "Erkennen durch Endzustand" bzw. mit "Erkennen durch leeren Stack" arbeiten, äquivalent sind.
Ein Stackautomat, der durch leeren Stack erkennt, lässt sich offenbar sehr einfach in einen Stackautomaten umformen, der durch Endzustand erkennt. Hierbei wird das zusätzliche Zeichen $ verwendet, um das untere Ende des Stacks zu kennzeichnen. Ist dieses Zeichen das obere Stackzeichen, so ist der Stack – bis auf dieses Zeichen – leer und der Stackautomat geht in einen Endzustand über.
Umgekehrt lässt sich ein Stackautomat, der durch Endzustand erkennt, in einen Stackautomaten umformen, der durch leeren Stack erkennt. Dies geschieht, indem die Übergangsrelation um zusätzliche Tupel erweitert wird, die ausgehend von jedem Endzustand ein Leeren des Stacks ermöglichen. Dies kann allerdings im Allgemeinen nur nichtdeterministisch geschehen. Ein deterministischer Stackautomat weiß im Allgemeinen nicht, ob er beim Erreichen eines Endzustands das Eingabewort schon zu Ende gelesen hat und er mit dem Leeren des Stacks beginnen soll.
Wir werden im Folgenden die Variante des Stackautomaten, der durch leeren Stack erkennt, des öfteren verwenden.
Aufgaben
Aufgabe 1: Sei A = {a, b} ein Alphabet und sei L ⊆ A* mit
L = { w | |w|a = |w|b }
die Sprache aller Wörter, die gleichviele a's und b's enthalten.
Geben Sie einen Stackautomaten an, der L durch leeren Stack erkennt. Achten Sie darauf, dass der Automat mindestens einen Zustandsübergang macht, bevor er das leere Wort erkennt.
1) Andere gebräuchliche Bezeichnungen sind: Kellerautomat, Pushdown-Automat
2) ... und dabei mindestens einen Zustandsübergang vollzogen hat. Denn sonst erkennt der Stackautomat grundsätzlich immer das Wort ε.
Weiter mit: [Konstruktion eines nichtdeterministischen Stackautomaten] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 26.01.2003 Updated: 16.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden