Theoretische Informatik
Turingmaschine
Die Turingmaschine ist ein sehr einfaches abstraktes Modell eines Computers – das gleichwohl mächtig genug ist, alles zu berechnen, was berechenbar ist.
Benannt ist die Turingmaschine nach A.M. Turing , der sie 1936 erdacht hat [Tur 36].
, der sie 1936 erdacht hat [Tur 36].
Idee
Das Maschinenmodell der Turingmaschine ist in Bild 1 dargestellt. Die Turingmaschine hat ein Steuerwerk, in dem sich das Programm befindet. Die Turingmaschine kann mit einem Schreib-/Lesekopf auf ein Arbeitsband zugreifen, sie kann dabei Zeichen auf dem Arbeitsband lesen und Zeichen auf das Arbeitsband schreiben. Ferner kann sie den Schreib-/Lesekopf nach links oder rechts bewegen.
Das Arbeitsband ist in Felder unterteilt. Der Anfang des Arbeitsbandes ist mit dem Bandbegrenzungszeichen $ gekennzeichnet; nach rechts ist das Arbeitsband unbeschränkt.
Zu Beginn der Verarbeitung steht am Anfang des Arbeitsbandes ein Eingabewort, die restlichen Felder des Arbeitsbandes enthalten das Leerzeichen  .
.
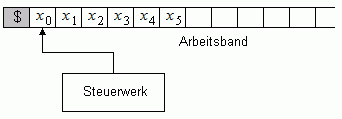
Bild 1: Turingmaschine mit Eingabewort x = x0 ... x5
Definition
Formal lässt sich die Turingmaschine wie folgt darstellen:
Definition: Eine Turingmaschine ist ein Tupel
M = (Z, E, A, d, q, F).
Hierbei ist
| Z | eine endliche, nichtleere Menge von Zuständen des Steuerwerks, | |
| E | das Eingabealphabet, | |
| A | das Arbeitsalphabet, wobei E ⊆ A, | |
| d | die Übergangsrelation d ⊆ Z × A × A' × Z; hierbei ist A' = A ∪ {L, R}, | |
| q ∈ Z | der Startzustand, | |
| F ⊆ Z | die Menge der Endzustände |
Das Arbeitsalphabet A enthält die speziellen Zeichen $ und  ; diese kommen nicht im Eingabealphabet vor. Die Zeichen L, R kommen nicht als Alphabetzeichen vor.
; diese kommen nicht im Eingabealphabet vor. Die Zeichen L, R kommen nicht als Alphabetzeichen vor.
Arbeitsweise
Die Elemente der Übergangsrelation d sind 4-Tupel der Form (s, a, a', s'). Diese stellen mögliche Zustandsübergänge der Turingmaschine dar, mit folgender Bedeutung: Wenn die Turingmaschine im Zustand s ist und das Zeichen a auf dem Arbeitsband liest, so überschreibt sie es mit dem Zeichen a' und geht in den Folgezustand s' über. Das Zeichen a' kann auch eines der Symbole L oder R sein; in diesem Fall schreibt die Turingmaschine nicht, sondern bewegt den Schreib-/Lesekopf nach links (L) oder nach rechts (R).
Wenn für jedes Paar, bestehend aus Zustand s und Zeichen a, höchstens ein solcher Zustandsübergang definiert ist, arbeitet die Turingmaschine deterministisch.
Es kann auch sein, dass für einen Zustand s und ein Zeichen a kein Folgezustand definiert ist; in diesem Fall hält die Turingmaschine, wenn sie sich im Zustand s befindet und das Zeichen a liest.
Die Turingmaschine wird im Startzustand q gestartet. Der Schreib-/Lesekopf befindet sich auf dem ersten Feld hinter dem Bandbegrenzungszeichen $. Dort steht das Eingabewort w auf dem Arbeitsband (siehe Bild 1).
Die Turingmaschine liest das erste Zeichen des Eingabewortes und führt von dort ausgehend die entsprechenden weiteren möglichen Zustandsübergänge durch. Dabei können zwei Situationen auftreten. Entweder kommt die Turingmaschine irgendwann zu einem Zustand, von dem aus mit dem gelesenen Zeichen kein weiterer Zustandsübergang definiert ist, d.h. die Turingmaschine hält, oder die Turingmaschine kommt nie zu einem solchen Zustand, d.h. sie läuft unendlich lange weiter.
Oder genauer ausgedrückt: Entweder gibt es eine Folge von Zustandsübergängen, beginnend beim Startzustand q und mit dem Eingabewort w auf dem Arbeitsband, die irgendwann abbricht, weil kein weiterer Zustandsübergang mehr möglich ist. Oder es gibt keine solche abbrechende Folge, d.h. alle Folgen von Zustandsübergängen sind unendlich lang.
Wenn es eine solche abbrechende Folge von Zustandsübergängen gibt und deren letzter erreichter Zustand in der Menge F der Endzustände liegt, so erkennt die Turingmaschine das Eingabewort w. Wenn jede solche abbrechende Folge von Zustandsübergängen in einem Nicht-Endzustand endet, so weist die Turingmaschine das Eingabewort w zurück. Wenn es nur unendlich lange Folgen von Zustandsübergängen gibt, so erkennt sie das Eingabewort nicht, weist es aber auch nicht zurück.
Im Gegensatz zum endlichen Automaten oder auch zum Stackautomaten ist es nicht erforderlich, dass das Eingabewort vollständig gelesen worden ist.
Definition: Die Menge aller Wörter, die von einer Turingmaschine M erkannt werden, heißt die von M erkannte Sprache; sie wird mit L(M) bezeichnet:
L(M) = { w ∈ E* | w wird von M erkannt }
Turingtabelle
Die Übergangsrelation d wird in Form einer Tabelle, der Turingtabelle, angegeben. Jedes Element (s, a, a', s') der Übergangsrelation ist eine Zeile in der Turingtabelle, mit folgender Bedeutung: Wenn die Turingmaschine im Zustand s ist und das Zeichen a liest, so schreibt sie das Zeichen a' (bzw. führt die Aktion a' aus, wenn a' = L oder a' = R ist) und geht in den Zustand s' über.
Beispiel: Die folgende Turingtabelle repräsentiert die Übergangsrelation d einer Turingmaschine M = (Z, E, A, d, q, F), die alle Eingabewörter der Form an mit n ∈ ℕ0 erkennt.
Die Zustandsmenge der Turingmaschine ist Z = {0, 1}, das Eingabealphabet ist E = {a, b}, das Arbeitsalphabet ist A = {a, b, $,  }, der Startzustand ist q = 0, die Menge der Endzustände ist F = {1}.
}, der Startzustand ist q = 0, die Menge der Endzustände ist F = {1}.
Die erste Zeile der Turingtabelle bedeutet: Wenn die Turingmaschine im Zustand 0 ist und das Zeichen a liest, so geht sie auf dem Arbeitsband um eine Position nach rechts und bleibt im Zustand 0. Die zweite Zeile bedeutet: Wenn die Turingmaschine im Zustand 0 ist und das Leerzeichen  liest, so überschreibt sie es mit dem Leerzeichen
liest, so überschreibt sie es mit dem Leerzeichen  und geht in den Zustand 1 über.
und geht in den Zustand 1 über.
Die Turingmaschine startet im Zustand 0. Wenn auf dem Arbeitsband als Eingabewort eine Folge von a's steht, so liest die Turingmaschine diese a's und bleibt dabei im Zustand 0. Wenn das Eingabewort zu Ende ist, liest die Turingmaschine das Leerzeichen  und geht in den Zustand 1 über. Vom Zustand 1 aus sind keine weiteren Zustandsübergänge möglich, d.h. die Turingmaschine hält. Da der Zustand 1 der Endzustand ist, erkennt sie das Eingabewort. Es kann auch sein, dass gleich das erste gelesene Zeichen das Leerzeichen ist, d.h. die Turingmaschine erkennt auch das leere Eingabewort a0 = ε.
und geht in den Zustand 1 über. Vom Zustand 1 aus sind keine weiteren Zustandsübergänge möglich, d.h. die Turingmaschine hält. Da der Zustand 1 der Endzustand ist, erkennt sie das Eingabewort. Es kann auch sein, dass gleich das erste gelesene Zeichen das Leerzeichen ist, d.h. die Turingmaschine erkennt auch das leere Eingabewort a0 = ε.
Ein Zustandsübergang für den Zustand 0 und das Zeichen b ist in der Turingtabelle nicht definiert. Dies führt dazu, dass die Turingmaschine hält, wenn sie im Zustand 0 ist und das Zeichen b liest. Da der Zustand 0 nicht der Endzustand ist, weist sie das Eingabewort in diesem Fall zurück.
Die von der Turingmaschine erkannte Sprache ist somit
L(M) = { an | n ∈ ℕ0 }.
Das Arbeitsband ist links durch das Bandbegrenzungszeichen $ begrenzt. Die Turingmaschine darf diese Begrenzung nicht überschreiten. Wenn sie also das Zeichen $ liest, darf sie nicht nach links gehen; sie darf das Zeichen $ auch nicht durch ein anderes Zeichen überschreiben. D.h. für die Übergangsrelation d muss gelten
(s, $, a', s') ∈ d ⇒ a' = R ∨ a' = $
Beispiele
Erkennung der Sprache { anbn | n ∈ ℕ }
Die folgende Turingmaschine erkennt die Sprache { anbn | n ∈ ℕ }. Sie liest solange a's, bis sie das erste b findet. Dann pendelt sie zwischen den a's und b's hin und her und löscht abwechselnd ein b und ein a.
Zum Schluss, wenn die Turingmaschine an das Ende der Eingabe kommt und ein Leerzeichen liest, überprüft sie, ob vorne noch ein überzähliges a vorhanden ist.
Der Zustand 4 ist Endzustand; ferner gibt es einen expliziten reject-Zustand, dieser ist durch ein - dargestellt.
Aufgaben
Aufgabe 1: Entwerfen Sie eine Turingmaschine , die alle Wörter der Form a2nbn mit n ∈ ℕ erkennt.
Simulieren Sie die Turingmaschine mit dem Turingmaschinen-Simulator.
Aufgabe 2: Entwerfen Sie eine Turingmaschine , die alle Wörter der Form a2n mit n ∈ ℕ0 erkennt.
Simulieren Sie die Turingmaschine mit dem Turingmaschinen-Simulator.
Aufgabe 3: Entwerfen Sie eine Turingmaschine, die alle aus a's und b's bestehenden Wörter erkennt, die korrekten Klammerstrukturen entsprechen, wobei a einer öffnenden und b einer schließenden Klammer entspricht. Die Turingmaschine soll also beispielsweise aababbab akzeptieren, aber abbabaab zurückweisen.
Simulieren Sie die Turingmaschine mit dem Turingmaschinen-Simulator.
Literatur
[Sip 96] M. Sipser: Introduction to the Theory of Computation. PWS Publishing Company (1996)
[Tur 36] A.M. Turing: On Computable Numbers, with an Application to the Entscheidungsproblem. Proceedings, London Mathematical Society, 230-265 (1936)
[Weg 99] I. Wegener: Theoretische Informatik -- eine algorithmische Einführung. 2. Auflage, Teubner (1999)
Weiter mit: [Chomsky-Hierarchie der Automaten] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 05.09.2004 Updated: 16.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden