Theoretische Informatik
String-Turingmaschine
Wir betrachten im Folgenden ein sehr einfaches abstraktes Modell einer Maschine zur Manipulation von Zeichenketten (Strings). Diese Maschine ist eine Variante der Turingmaschine, sie wird daher als String-Turingmaschine bezeichnet [Lan 10].
Idee
Das Maschinenmodell der String-Turingmaschine ist in Bild 1 dargestellt. Die Maschine hat ein Steuerwerk, in dem sich das Programm befindet. Sie kann auf die einzelnen Zeichen einer Zeichenkette, des Arbeitsstrings, zugreifen; dabei kann sie das jeweilige Zeichen lesen und durch ein anderes Zeichen überschreiben. Die Position des Zugriffs auf den Arbeitsstring wird als die Cursor-Position bezeichnet.
Ferner kann die Maschine die Cursor-Position jeweils um eine Position nach links oder rechts bewegen, an der Cursor-Position ein Leerzeichen einfügen oder das Zeichen an der Cursor-Position löschen. Diese Aktionen werden als Cursor-Aktionen bezeichnet. Es gibt somit die Cursor-Aktionen Links (L), Rechts (R), Einfügen (I – insert) und Löschen (D – delete).
Zu Beginn der Verarbeitung besteht der Arbeitsstring aus dem Eingabewort x zuzüglich einer Anfangsmarkierung $ und einer Endemarkierung &.
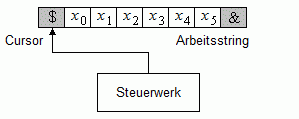
Bild 1: String-Turingmaschine mit Eingabewort x = x0 ... x5
Das Interessante an diesem Konzept besteht darin, dass String-Turingmaschinen, deren zulässige Cursor-Aktionen geeignet eingeschränkt werden, genau die Sprachklassen der Chomsky-Hierarchie erkennen (Bild 2). Beispielsweise erkennen String-Turingmaschinen, die lediglich die Cursor-Aktionen R und D verwenden, genau die Typ-2-Sprachen oder kontextfreien Sprachen.
| Sprachklasse | Cursor-Aktionen |
|---|---|
| Typ 0 | I, L, R, D |
| Typ 1 | L, R, D |
| Typ 2 | R, D |
| Typ 3 | D |
Bild 2: Zulässige Cursor-Aktionen von String-Turingmaschinen
Einfüge- und Löschaktion
Die Einfüge-Aktion I bewirkt, dass an der Cursor-Position das Leerzeichen  in den Arbeitsstring eingefügt wird. Das zuvor dort befindliche Zeichen und alle Zeichen links davon rücken um eine Position nach links (Bild 3a). Die Lösch-Aktion D bewirkt, dass alle Zeichen links von der Cursor-Position um eine Position nach rechts rücken. Das zuvor an der Cursor-Position befindliche Zeichen wird dabei überschrieben (Bild 3b).
in den Arbeitsstring eingefügt wird. Das zuvor dort befindliche Zeichen und alle Zeichen links davon rücken um eine Position nach links (Bild 3a). Die Lösch-Aktion D bewirkt, dass alle Zeichen links von der Cursor-Position um eine Position nach rechts rücken. Das zuvor an der Cursor-Position befindliche Zeichen wird dabei überschrieben (Bild 3b).
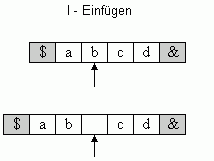
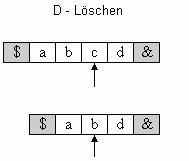
Bild 3: (a) Einfügen und (b) Löschen eines Zeichens
Formale Definition
Formal lässt sich die String-Turingmaschine wie folgt darstellen:
Definition: Eine nichtdeterministische String-Turingmaschine ist ein 6-Tupel
M = (Z, E, A, d, q, p).
Hierbei ist
| Z | eine endliche, nichtleere Menge von Zuständen des Steuerwerks, | |
| E | das Eingabealphabet, | |
| A | das Arbeitsalphabet, wobei E ⊆ A, | |
| d | die Übergangsrelation d ⊆ Z × A × A' × Z, hierbei ist A' = A ∪ {L, R, I, D}, | |
| q ∈ Z | der Startzustand, | |
| p ∈ {$, &} | das Zeichen an der Anfangsposition des Cursors |
Im Arbeitsalphabet A sind die Begrenzungszeichen $ und & sowie das Leerzeichen  enthalten; diese kommen nicht im Eingabealphabet vor. Die Zeichen L, R, I, D für die Cursor-Aktionen kommen nicht als Alphabetzeichen vor.
enthalten; diese kommen nicht im Eingabealphabet vor. Die Zeichen L, R, I, D für die Cursor-Aktionen kommen nicht als Alphabetzeichen vor.
Arbeitsweise
Zu Beginn besteht der Arbeitsstring aus dem Eingabewort, eingeschlossen von den Begrenzungszeichen $ und &. Je nach dem, ob das Eingabewort von links nach rechts oder von rechts nach links abgearbeitet werden soll, steht der Cursor zu Beginn auf der Anfangsmarkierung $ oder der Endemarkierung &.
Die Elemente der Übergangsrelation d sind 4-Tupel der Form (s, a, a', s'). Diese stellen mögliche Zustandsübergänge der String-Turingmaschine dar, mit folgender Bedeutung: Wenn die String-Turingmaschine im Zustand s ist und das Zeichen a an der Cursor-Position liest, so kann sie das Zeichen a mit dem Zeichen a' überschreiben und in den Folgezustand s' übergehen. Wenn jedoch das Zeichen a' eines der Symbole L, R, I oder D ist, dann schreibt die String-Turingmaschine nicht, sondern bewegt den Cursor nach links (L) oder nach rechts (R) oder fügt ein Leerzeichen an der Cursor-Position ein (I) oder löscht das Zeichen an der Cursor-Position (D).
Es kann mehrere mögliche Zustandsübergänge in einem Zustand s mit gelesenem Zeichen a geben; in diesem Fall verhält sich die String-Turingmaschine nichtdeterministisch.
Erkennung von Sprachen
Definition: Sei M eine String-Turingmaschine mit Eingabealphabet E.
Die String-Turingmaschine M erkennt ein Eingabewort x ∈ E, wenn es eine Folge von Zustandsübergängen gibt, durch die das Wort x einschließlich der beiden Begrenzungszeichen vollständig gelöscht wird.
Die von M erkannte Sprache L(M) ist die Menge aller Wörter x ∈ E, die von M erkannt werden:
L(M) = { x ∈ E | M erkennt x }
Beispiel: Sei L die Sprache aller korrekten Klammerstrukturen, wobei a für eine öffnende und b für eine schließende Klammer steht. Beispielsweise gehört das Wort aabbab zu L, jedoch abbaab nicht.
Die folgende String-Turingmaschine M = (Z, E, A, d, q, p) erkennt die Sprache L. Zustandsmenge ist Z = {0, 1, 2, 3}, Eingabealphabet E = {a, b}, Arbeitsalphabet A = {a, b, $, &  }; der Anfangszustand ist q = 0, zu Anfang zeigt der Cursor auf das Zeichen p = $, und die Übergangsrelation d ist wie folgt definiert:
}; der Anfangszustand ist q = 0, zu Anfang zeigt der Cursor auf das Zeichen p = $, und die Übergangsrelation d ist wie folgt definiert:
| s | a | a' | s' |
|---|---|---|---|
| 0 | $ | R | 0 |
| 0 | a | R | 0 |
| 0 | b | D | 1 |
| 0 | & | D | 2 |
| 1 | a | D | 0 |
| 2 | $ | D | 3 |
Bild 4 zeigt als Beispiel die Startsituation der String-Turingmaschine mit dem Eingabewort aabb. Die String-Turingmaschine startet im Zustand 0 und bewegt den Cursor solange nach rechts, bis sie auf das erste b trifft. Sie löscht dieses und geht in den Zustand 1 über. Im Zustand 1 erwartet die String-Turingmaschine ein zugehöriges a; sie löscht dieses ebenfalls und geht wieder in den Zustand 0. Damit hat sie ein inneres Klammerpaar gelöscht und beginnt von vorne. Stößt die String-Turingmaschine im Zustand 0 irgendwann auf die Endemarkierung &, so löscht sie diese und geht in den Zustand 2 über. Im Zustand 2 erwartet sie die Anfangsmarkierung $. Sie löscht diese ebenfalls und geht in den Zustand 3 über.
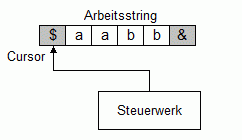
Bild 4: Startsituation mit Eingabewort aabb
Wenn das Eingabewort x in der Sprache L enthalten ist, so gelingt es der String-Turingmaschine M, durch eine Folge der beschriebenen Zustandsübergänge das Wort x einschließlich der Begrenzungszeichen $ und & zu löschen. Wenn dagegen das Eingabewort x nicht in der Sprache L enthalten ist, so gelingt es der String-Turingmaschine nicht, das Wort x einschließlich der Begrenzungszeichen $ und & zu löschen. Sie gerät dann irgendwann in einen Zustand, von dem aus mit dem Zeichen an der Cursor-Position kein Zustandsübergang möglich ist, dabei aber das Wort noch nicht vollständig gelöscht ist.
Besteht beispielsweise das Eingabewort nur aus einem a, so bewegt die String-Turingmaschine den Cursor solange nach rechts, bis sie auf die Endemarkierung & trifft. Sie löscht diese und geht in den Zustand 2 über. Im Zustand 2 trifft sie nun aber auf das a. Sie kann keinen Zustandsübergang mehr ausführen, hat aber das Eingabewort nicht gelöscht. Somit erkennt sie das Wort a nicht.
Diese String-Turingmaschine kann hier simuliert werden:
Die String-Turingmaschine aus diesem Beispiel verwendet nur zwei der vier möglichen Cursor-Aktionen L, R, I, D, nämlich R und D. Dies ist kein Zufall, denn die Sprache L der korrekten Klammerstrukturen aus dem Beispiel ist eine kontextfreie Sprache, und jede kontextfreie Sprache lässt sich, wie wir noch sehen werden, durch eine String-Turingmaschine erkennen, die nur die Cursor-Aktionen R und D benutzt.
String-Turingmaschine als Reduktionsmaschine
Gegeben sei eine Grammatik G. Dann lässt sich eine String-Turingmaschine konstruieren, die in der Lage ist, Reduktionen auszuführen, d.h. in ihrem Arbeitsstring jeweils die rechte Seite einer Produktion der Grammatik durch die zugehörige linke Seite zu ersetzen.
Die String-Turingmaschine erkennt dann ein Wort x ∈ L(G), indem sie es durch Anwendung der Produktionen von G auf das Startsymbol S reduziert und anschließend den verbleibenden String $S& löscht.
Für ein Wort x ∉ L(G) gibt es in G keine Reduktionsfolge auf das Startsymbol; daher gelingt es der String-Turingmaschine nicht, ein solches Eingabewort x vollständig zu löschen, sie erkennt es somit nicht.
Beispiel: Gegeben sei die Grammatik G mit folgenden Produktionen:
| S |  | aSb | ab |
| ab |  | ba |
Die Grammatik G erzeugt die Sprache aller nichtleeren Wörter über {a, b}, die gleich viele a's wie b's enthalten:
L(G) = { w ∈ {a, b}+ | |w|a = |w|b }
Eine entsprechende String-Turingmaschine M, die L(G) erkennt, ist im Folgenden angegeben. Zunächst hat M Zustandsübergänge, die es ihr ermöglichen, die Cursor-Position in ihrem String nach rechts und nach links zu bewegen:
| s | a | a' | s' |
|---|---|---|---|
| 0 | $ | R | 0 |
| 0 | a | R | 0 |
| 0 | b | R | 0 |
| 0 | S | R | 0 |
| 0 | & | L | 0 |
| 0 | a | L | 0 |
| 0 | b | L | 0 |
| 0 | S | L | 0 |
Die String-Turingmaschine arbeitet nichtdeterministisch; sie hat die Wahl, die Cursor-Position nach links oder nach rechts zu bewegen, wenn sie beispielsweise im Zustand 0 das Zeichen a liest.
Ferner hat die String-Turingmaschine M Zustandsübergänge, die es ihr ermöglichen, die Produktionen der Grammatik G anzuwenden.
So hat sie beispielsweise die Möglichkeit, wenn sie das Zeichen a liest, die Produktion ab ba anzuwenden, indem sie deren rechte Seite ba durch die linke Seite ab ersetzt:
ba anzuwenden, indem sie deren rechte Seite ba durch die linke Seite ab ersetzt:
| s | a | a' | s' |
|---|---|---|---|
| 0 | a | b | 1 |
| 1 | b | L | 2 |
| 2 | b | a | 0 |
Außerdem hat sie die Möglichkeit, wenn sie das Zeichen b liest, die Produktion S ab oder die Produktion S
ab oder die Produktion S aSb anzuwenden, indem sie die jeweilige rechte Seite durch die linke Seite S ersetzt:
aSb anzuwenden, indem sie die jeweilige rechte Seite durch die linke Seite S ersetzt:
| s | a | a' | s' |
|---|---|---|---|
| 0 | b | D | 3 |
| 3 | a | S | 0 |
| 3 | S | D | 4 |
| 4 | a | S | 0 |
Schließlich hat M noch Zustandsübergänge, die es ihr ermöglichen, zum Schluss den String $S& zu löschen:
| s | a | a' | s' |
|---|---|---|---|
| 0 | & | D | 5 |
| 5 | S | D | 6 |
| 6 | $ | D | 7 |
Diese vier Tabellen zusammengenommen bilden die Übergangsrelation der String-Turingmaschine.
Zu betonen ist in diesem Zusammenhang noch einmal die Tatsache, dass die String-Turingmaschine nichtdeterministisch arbeitet. Sie erkennt das Eingabewort nur dann, wenn sie jeweils die richtigen Zustandsübergänge wählt. Dies ist kennzeichnend für die nichtdeterministischen Arbeitsweise: Es ist gefordert, dass es eine Folge von Zustandsübergängen gibt, die zum gewünschten Ergebnis führt, nicht jedoch, dass jede Folge von möglichen Zustandsübergängen zum gewünschten Ergebnis führt.
Im Übrigen ist auch die Ableitung eines Wortes mithilfe der Produktionen einer Grammatik im Allgemeinen ein nichtdeterministischer Vorgang. Sobald nämlich eine Produktion mehrere Alternativen hat, besteht ebenfalls eine Wahlmöglichkeit und es muss die richtige Wahl getroffen werden, um das Wort erfolgreich abzuleiten. In der Grammatik G aus dem obigen Beispiel lässt sich z.B. das Wort aabb nur dann aus dem Startsymbol S ableiten, wenn als erster Ableitungsschritt S aSb gewählt wird (und nicht der ebenfalls mögliche Ableitungsschritt S
aSb gewählt wird (und nicht der ebenfalls mögliche Ableitungsschritt S ab).
ab).
Zusammenfassung
Mithilfe der Produktionen einer Grammatik G = (V, T, P, S) lassen sich Wörter ableiten. Die Menge der Wörter über T, die sich mithilfe der Produktionen von G aus dem Startsymbol S ableiten lassen, ist die von G erzeugte Sprache L(G). Umgekehrt lassen sich alle Wörter aus L(G) durch umgekehrtes Durchlaufen ihrer Ableitungsfolge auf das Startsymbol S reduzieren. Ein Wort über T, das nicht zu L(G) gehört, lässt sich dagegen nicht auf S reduzieren (denn sonst ließe es sich auch aus S ableiten).
Das Konzept der String-Turingmaschine ist dazu geeignet, die Reduktion von Wörtern auf das Startsymbol maschinell nachzubilden. Das Interessante an diesem Konzept wird auf den folgenden Seiten deutlich. Wenn die Menge {L, R, I, D} der Cursor-Aktionen geeignet eingeschränkt wird, ergeben sich nämlich Typ-i-String-Turingmaschinen, die genau die Sprachen der entsprechenden Sprachklasse der Chomsky-Hierarchie erkennen. Werden beispielsweise die Cursor-Aktionen auf {R, D} eingeschränkt, ergeben sich Typ-2-String-Turingmaschinen, die genau die kontextfreien Sprachen erkennen.
Literatur
[Lan 10] H.W. Lang: A Characterization of the Chomsky Hierarchy by String Turing Machines. In: H.R. Arabnia, G.A. Gravvanis, A.M.G. Solo (Hrsg.): Proceedings of the 2010 International Conference on Foundations of Computer Science, CSREA Press, 109-114 (2010)
Weiter mit: [Chomsky-Hierarchie der String-Turingmaschinen] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 25.08.2010 Updated: 16.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden