Kryptografische Protokolle
Teilnehmer-Authentifizierung mit Zero-Knowledge-Protokoll
Wenn zwei Teilnehmer A und B miteinander kommunizieren, wie kann sich dann A sicher sein, wirklich mit B zu kommunizieren, und nicht mit C, der sich als B ausgibt? Und umgekehrt: Wie kann sich B sicher sein, wirklich mit A zu kommunizieren? Dies ist das Problem der Teilnehmer-Authentifizierung.
Graph-Isomorphismus-Protokoll
Das Bit-Commitment-Protokoll aus dem letzten Abschnitt basiert auf der Isormorphie von Graphen. Es kann von zwei Teilnehmern A und B verwendet werden, um eine Münze zu werfen. A legt sich auf i fest, B wählt j, A deckt i auf und hat gewonnen, wenn i = j ist.
Was ist, wenn dieses Protokoll n-mal wiederholt wird und A jedes Mal gewinnt? Es könnte Zufall sein – die Wahrscheinlichkeit dafür ist allerdings gering, nämlich 1 : 2n. Oder aber A ist in der Lage zu täuschen. Dann aber kennt er einen Isomorphismus zwischen den zugrunde liegenden Graphen G0 und G1.
Je öfter also das Protokoll wiederholt wird, wobei jedes Mal A gewinnt, desto sicherer ist sich B, dass A einen Isomorphismus zwischen G0 und G1 kennt.
Das Protokoll kann somit von Teilnehmer A verwendet werden, um sich zu authentifizieren. Er kann beweisen, dass er einen Isomorphismus zwischen den beiden Graphen kennt; dies ist sein Identitätsmerkmal.
Beim Bit-Commitment erzeugt Teilnehmer B die beiden Graphen, um sicherzustellen, dass niemand anderer den Isomorphismus kennt (und dadurch täuschen kann). Bei der Teilnehmer-Authentifizierung erzeugt A die beiden Graphen, um sicherzustellen, dass niemand anderer den Isomorphismus kennt (und dadurch sich als A ausgeben kann).
Zero-Knowledge-Eigenschaft
Teilnehmer A braucht dabei jedoch den Isomorphismus selbst nicht preiszugeben. Tatsächlich ist es sogar so, dass ein Dritter C, der den Nachrichtenaustausch zwischen A und B abhört, daraus überhaupt keine Information gewinnt. Dies wird daran deutlich, dass ein Vierter D den Nachrichtenaustausch zwischen A und B simulieren könnte, ohne dass C dies merken würde.
Hierzu muss D lediglich in jeder Runde ein zufälliges Bit j und einen zufälligen Isomorphismus h wählen, H = h(Gj) berechnen und an B senden, daraufhin das gewählte Bit j an A senden und daraufhin h an B senden (Bild 1).
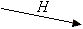 | ||||
| A | 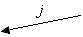 | B | ||
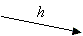 |
Bild 1: Bit-Commitment-Protokoll
Einem Außenstehenden C erscheint es so, als ob A sich durch Senden des Graphen H auf ein bestimmtes Bit festlegt, als ob daraufhin B ein zufälliges Bit j würfelt, und als ob daraufhin A zeigt, dass er sich auf eben dieses j festgelegt hat, indem er nämlich den Isomorphismus h mit H = h(Gj) offenbart.
Da D keinerlei Information, die C nicht auch hat, in den simulierten Nachrichtenaustausch hineinsteckt, kann C auch keine Information aus dem Nachrichtenaustausch herausholen. Ein Protokoll, aus dessen Nachrichtenaustausch keine Information gewonnen werden kann, hat die Zero-Knowledge-Eigenschaft.
Literatur
[BSW 95] A. Beutelspacher, J. Schwenk, K.D. Wolfenstetter: Moderne Verfahren der Kryptographie. Vieweg (1995)
[Lan 18] H.W. Lang: Kryptografie für Dummies. Wiley (2018)
Weiter mit: [Fiat-Shamir-Protokoll] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 04.12.2003 Updated: 17.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden
