Zahlentheoretische Grundlagen der Kryptografie
Graphisomorphismus
Zwei ungerichtete Graphen G = (V, E) und G' = (V', E') sind gleich, wenn sie dieselbe Knotenmenge und dieselbe Kantenmenge haben, d.h. wenn V = V' und E = E' gilt.
Die beiden folgenden Graphen G und G' sehen zwar gleich aus, sie sind aber nicht gleich (Bild 1). Denn in G sind z.B. die Knoten 0 und 4 durch eine Kante verbunden, während dies in G' nicht der Fall ist.
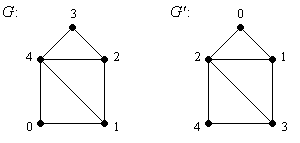
Bild 1: Zwei gleich aussehende Graphen
Zwei Graphen, die man so zeichnen kann, dass sie gleich aussehen, werden als isomorph (von gleicher Gestalt) bezeichnet. Formal ist die Isomorphie zwischen zwei Graphen wie folgt definiert.
Definition: Zwei ungerichtete Graphen G = (V, E) und G' = (V', E') sind isomorph, wenn es eine bijektive Abbildung
f : V → V'
gibt, derart dass
(u, v) ∈ E ⇔ (f(u), f(v)) ∈ E'
gilt. Eine solche Abbildung heißt Isomorphismus zwischen den Graphen G und G'.
Im Folgenden setzen wir der Einfachheit halber voraus, dass V = V' ist. Die Abbildung f ist dann eine Permutation der Knotenmenge V.
Bei den beiden Graphen in Bild 1 ist die Permutation der Knotenmenge implizit dadurch gegeben, dass die einander zugeordneten Knoten jeweils an entsprechende Stellen gezeichnet sind (z.B. die 3 und die 0 oben usw.). Die entsprechende Abbildung ist
| v: | 0 | 1 | 2 | 3 | 4 | |
| f(v): | 4 | 3 | 1 | 0 | 2 |
Wenn die Abbildung zwischen den Knoten nicht bekannt ist, so ist es nicht ohne Weiteres möglich, die einander zugeordneten Knoten an entsprechende Stellen zu zeichnen. Es bleibt dann nichts anderes übrig, als die Knoten von G' in irgendeiner Anordnung zu zeichnen, z.B. in derselben Anordnung wie die Knoten von G. Dann ist es weitaus weniger offensichtlich, dass die Graphen isomorph sind (Bild 2).
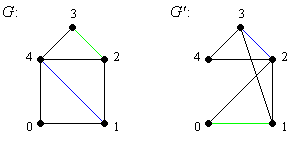
Bild 2: Zwei isomorphe Graphen
Jeder Kante (u, v) in G entspricht die Kante (f(u), f(v)) in G' und umgekehrt.
Beispielsweise entspricht der blau dargestellten Kante(1, 4) in G die Kante (f(1), f(4)) = (3, 2) in G'. Der grün dargestellten Kante (2, 3) in G entspricht die Kante (f(2), f(3)) = (1, 0) in G'.
Ein Graphisomorphismus ist ein anschauliches Beispiel für eine Einwegfunktion. Es ist leicht, zu einem gegebenen Graphen G einen isomorphen Graphen G' zu konstruieren (indem einfach die Knotenmenge von G permutiert wird). Umgekehrt dagegen ist es jedoch schwer, zu zwei gegebenen isomorphen Graphen G und G' einen Isomorphismus zu rekonstruieren. Es bleibt im Allgemeinen nicht viel anderes übrig, als alle möglichen Permutationen der Knotenmenge auszuprobieren. Jedenfalls ist zur Zeit kein wesentlich schnellerer Algorithmus bekannt.
Die Graphen dürfen allerdings nicht wie in obigem Beispiel beschaffen sein. Im Beispiel hat G nur einen einzigen Knoten, von dem 4 Kanten ausgehen, also vom Grad 4, nämlich den Knoten 4. Es ist klar, dass ein Isomorphismus zwischen G und G' Knoten 4 auf Knoten 2 abbildet, nämlich den entsprechenden einzigen Knoten vom Grad 4 in G'.
Weiterhin gibt es je zwei Knoten vom Grad 3 und zwei Knoten vom Grad 2. Auch diese müssen jeweils aufeinander abgebildet werden. Es brauchen also bei diesen Graphen längst nicht alle möglichen Permutationen ausprobiert werden, sondern nur sehr viel weniger.
Wenn jedoch in den beiden Graphen alle Knoten denselben Grad haben, dann helfen derartige Überlegungen nicht weiter.
Weiter mit: [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 22.11.2003 Updated: 17.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden