Kryptografische Protokolle
Bit-Commitment
Commitment bedeutet Festlegung. Bei einer öffentlichen Ausschreibung beispielsweise legt jeder Anbieter sich auf sein Angebot fest, gibt dieses aber zunächst noch nicht preis (indem er es in einem verschlossenen Umschlag abgibt). Erst nach Ende der Ausschreibungsfrist wird die Festlegung offenbart (der Umschlag geöffnet). Gewährleistet ist so, dass während der Ausschreibung die Konkurrenten nichts über die Höhe der Angebote der anderen erfahren und dass die Angebote verbindlich sind, d.h. nachträglich nicht mehr geändert werden können.
Im Folgenden geht es darum, wie sich eine solche Festlegung (zunächst nur auf ein Bit 0 oder 1) mit kryptografischen Verfahren realisieren lässt.
Werfen einer Münze
Das Werfen einer Münze kann, wenn gerade keine Münze zur Hand ist, wie folgt realisiert werden. Jeder der beiden Teilnehmer A und B denkt sich eine Zahl aus der Menge {0, 1}. Sind die beiden gedachten Zahlen gleich, hat A gewonnen, sind sie verschieden, hat B gewonnen.
Das Problem ist, dass sich A und B die Zahlen mitteilen müssen, um zu entscheiden, wer gewonnen hat. Sagt B als erster zum Beispiel: "Ich habe die 1", so könnte A versucht sein, zu antworten: "Tja, tut mir leid, ich habe auch die 1", obwohl er sie gar nicht hatte.
Die Lösung besteht in folgendem Protokoll.
A schreibt seine Zahl auf einen Zettel und legt den Zettel verdeckt auf den Tisch. A hat sich damit auf seine Zahl festgelegt, aber B kennt die Zahl noch nicht. Nun erst nennt B seine Zahl. Daraufhin offenbart A seine Festlegung, indem er den Zettel zeigt. B prüft, welche Zahl auf dem Zettel steht.
Auch hier gibt es Möglichkeiten zu täuschen. So könnte B beispielsweise versuchen, heimlich unter den Zettel zu schauen. Oder A könnte versuchen, nachdem er B's Zahl erfahren hat, den Zettel gegen einen anderen auszutauschen, bevor er ihn zeigt.
Bei der kryptografischen Realisierung dieses Protokolls müssen entsprechende Täuschungsmöglichkeiten ausgeschlossen werden.
Bit-Commitment-Protokoll
Das Problem bei der kryptografischen Realisierung ist, wie sich A auf ein Bit i ∈ {0, 1} festlegen kann, ohne dieses Bit preiszugeben, und wie er anschließend beweisen kann, dass er sich tatsächlich auf dieses Bit festgelegt hatte. Diese Aufgabe wird als commitment (verbindliche Festlegung) bezeichnet.
Bei dem folgenden Protokoll (Bild 1) werden zwei isomorphe Graphen zugrunde gelegt. Für dieses Protokoll ist es wichtig, dass A keinen Isomorphismus zwischen den beiden Graphen kennt. Dies ist gewährleistet, wenn B die beiden Graphen erzeugt und den Isomorphismus geheimhält, und wenn die Graphen so groß sind, dass die Berechnung des Isomorphismus praktisch undurchführbar ist.
| A | B | |||||||||||
| isomorphe Graphen G0 und G1 | ||||||||||||
| wählt zufällig i ∈ {0, 1} und Isomorphismus h | ||||||||||||
| berechnet H = h(Gi) | Festlegung | |||||||||||
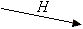 | ||||||||||||
| (versucht, die Festlegung aufzudecken) | ||||||||||||
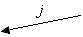 | wählt j ∈ {0, 1} | |||||||||||
| (versucht, die Festlegung zu fälschen) | Offenbaren der Festlegung | |||||||||||
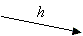 | ||||||||||||
| prüft | ||||||||||||
|
Bild 1: Bit-Commitment-Protokoll
Das Protokoll besteht im Wesentlichen aus zwei Phasen, der Festlegung und dem Offenbaren der Festlegung. Zwischendurch sendet B das Bit j, das er gewählt hat.
Sicherheit des Protokolls
In der ersten Phase legt sich Teilnehmer A auf i ∈ {0, 1} fest, indem er einen zufälligen Isomorphismus h auf den entsprechenden Graphen Gi anwendet und das Ergebnis, den Graphen H, an Teilnehmer B sendet.
Um herauszufinden, auf welches i sich A festgelegt hat, müsste B herausfinden, ob H aus G0 oder aus G1 hervorgegangen ist. Dies ist jedoch unmöglich, da G0 und G1 isomorph sind.
Es ist also für Teilnehmer B unmöglich, die Festlegung vorzeitig aufzudecken.
Nachdem B sein Bit j gesendet hat, offenbart nun Teilnehmer A in der zweiten Phase die Festlegung, indem er den verwendeten Isomorphismus an B sendet. Teilnehmer B berechnet h-1(H) und weiß nun, auf welches i sich A festgelegt hatte, je nachdem, ob das Ergebnis G0 oder G1 ist.
Teilnehmer A kann jedoch versuchen zu täuschen, indem er einen Isomorphismus g sendet, für den gilt g -1(H) = Gj , j ≠ i. Einen solchen Isomorphismus g zu finden, ist aber mindestens genauso schwer, wie einen Isomorphismus zwischen G0 und G1 zu finden, denn es gilt
Gj = g -1(H) = g -1(h(Gi)).
D.h. wenn A den Isomorphismus g hat, dann hat er auch den Isomorphismus zwischen Gi und Gj, nämlich f = hg -1 (Bild 2).
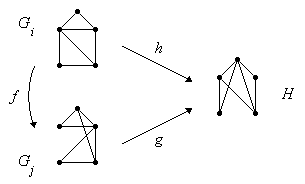
Bild 2: Isomorphismen zwischen Gi , Gj und H
Das Problem, einen Isomorphismus f zwischen zwei isomorphen Graphen zu bestimmen, ist jedoch schwer zu lösen. Es ist kein Verfahren bekannt, dessen Rechenaufwand polynomiell bezogen auf die Anzahl der Knoten der Graphen ist.
Es ist also für Teilnehmer A praktisch undurchführbar, die Festlegung zu fälschen.
Realisierung des Münzwurfs
Das Werfen einer Münze wird mit Hilfe des angegebenen Bit-Commitment-Protokolls also wie folgt realisiert:
- A legt sich auf i ∈ {0, 1} fest;
- B wählt j ∈ {0, 1};
- A hat gewonnen, wenn er durch Offenbaren der Festlegung beweisen kann, dass er sich auf i = j festgelegt hatte; ansonsten hat B gewonnen.
Im nächsten Abschnitt wird gezeigt, wie sich aus diesem Bit-Commitment-Protokoll ein Protokoll zur Teilnehmer-Authentifizierung ableiten lässt.
Literatur
[BSW 95] A. Beutelspacher, J. Schwenk, K.D. Wolfenstetter: Moderne Verfahren der Kryptographie. Vieweg (1995)
[Lan 18] H.W. Lang: Kryptografie für Dummies. Wiley (2018)
Weiter mit: [Zero-Knowledge-Protokoll zur Teilnehmer-Authentifizierung] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 23.11.2003 Updated: 17.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden
