Kryptografische Protokolle

Die Sicherheit des eben dargestellten Bit-Commitment-Protokolls auf Basis von Graphen beruht darauf, dass es schwierig ist, einen Isomorphismus zwischen zwei gegebenen isomorphen Graphen zu bestimmen. Nun sind große Graphen wegen der damit verbundenen Datenmengen für praktische Zwecke allerdings nicht gut geeignet.

Das Fiat-Shamir-Protokoll ist ein ganz entsprechendes Protokoll, dessen Sicherheit darauf beruht, dass es schwierig ist, Quadratwurzeln modulo n zu berechnen, wenn n das Produkt von zwei verschiedenen Primzahlen p und q ist.

Bit-Commitment-Protokoll

Es geht wiederum darum, dass sich A auf ein Bit 0 oder 1 festlegt, ohne es zunächst preiszugeben. Erst wenn B sein Bit genannt hat, offenbart A seine Festlegung.

Die Zahl n ist das Produkt von zwei verschiedenen Primzahlen p und q; die Zahl s ist eine Quadratzahl¹) in ℤ_n*, d.h. es gilt s = v² mod n für ein v ∈ ℤ_n*. Es muss ferner gelten, dass s ≠ 1 ist.

A				B
		Zahlen n und s
wählt zufällig    i ∈ {0, 1}  und    r ∈ ℤn*  mit  r ≠ ±1
berechnet    x =  r2 mod n     falls i = 0 r2s mod n     falls i = 1
		Festlegung
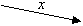				(versucht, die Festlegung aufzudecken)
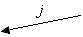				wählt    j ∈ {0, 1}
(versucht, die Festlegung zu fälschen)		Offenbaren der Festlegung
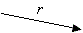				prüft   ob  x = r2 mod n ( ⇒ i = 0 )   oder   x = r2s mod n  ( ⇒ i = 1 )

Sicherheit

Wiederum ist zu prüfen, ob B die Festlegung aufdecken kann und ob A täuschen kann. Sicherlich kann B die Festlegung nicht aufdecken, denn es ist für ihn unmöglich, r² mod n und r²s mod n zu unterscheiden, denn beides sind Quadratzahlen modulo n.

A gelingt es zu täuschen, wenn er statt r eine Zahl t sendet, für die (modulo n gerechnet) gilt t²s = x = r² bzw. t² = x = r²s. Dann aber ist r = ts bzw. t = rs. In beiden Fällen kann A, wenn er t kennt, auch s berechnen. Dieses t zu berechnen ist also mindestens so schwer wie s, die Quadratwurzel modulo n von s, zu berechnen.

Das Protokoll ist also dann sicher, wenn A keine Quadratwurzel modulo n von s kennt. Daher sollte B die Zahl s wählen. Für große n ist es für A praktisch undurchführbar, die Wurzel modulo n aus der Zahl s zu ziehen.

Teilnehmer-Authentifizierung

Wenn umgekehrt nur A eine Quadratwurzel modulo n von s kennt, kann sich A durch dieses Wissen authentifizieren. Das entsprechende Protokoll zur Teilnehmer-Authentifizierung besteht wieder aus n Würfel-Runden, bei denen A jedes Mal gewinnt. Durch die Kenntnis von s kann A jedes Mal gewinnen: er deckt seine Festlegung korrekt auf, wenn i = j ist, und er täuscht, wenn i ≠ j ist, indem er t = rs bzw. t = rs ^-1 sendet.

Zero-Knowledge-Eigenschaft

Teilnehmer A braucht die Zahl s nicht preiszugeben. Wiederum ist es so, dass ein Dritter C, der den Nachrichtenaustausch zwischen A und B abhört, daraus keine Information gewinnt. Dies wird daran deutlich, dass ein Vierter D den Nachrichtenaustausch zwischen A und B simulieren könnte, ohne dass C dies merken würde.

Hierzu muss D lediglich in jeder Runde ein zufälliges Bit j und eine zufällige Zahl r wählen, in Abhängigkeit von j entweder x = r² oder x = r²s berechnen und an B senden, daraufhin das gewählte Bit j an A senden und daraufhin r an B senden. Einem Außenstehenden C erscheint es so, als ob A sich durch Senden von x auf ein bestimmtes Bit festlegt, als ob daraufhin B ein zufälliges Bit j würfelt, und als ob daraufhin A aufdeckt, dass er sich auf eben dieses j festgelegt hat, indem er die Zahl r offenbart.

Da D keinerlei Information, die C nicht auch hat, in den simulierten Nachrichtenaustausch hineinsteckt, kann C auch keine Information aus dem Nachrichtenaustausch herausholen. Das Protokoll hat also die Zero-Knowledge-Eigenschaft.

Literatur

Originalartikel:

[FS 87]   A. Fiat, A. Shamir: How to Prove Yourself: Practical Solutions to Identification and Signature Problems. In: A.M. Odlyzko (ed.): Advances in Cryptology - CRYPTO’ 86. Lecture Notes in Computer Science 263, 186-194 (1987)

Bücher:

[BNS 05]   A. Beutelspacher, H.B. Neumann, T. Schwarzpaul: Kryptografie in Theorie und Praxis. Vieweg (2005)

[Ert 12]   W. Ertel: Angewandte Kryptographie. 4. Auflage, Hanser (2012)

[Lan 18]   H.W. Lang: Kryptografie für Dummies. Wiley (2018)

[Weitere Informationen]