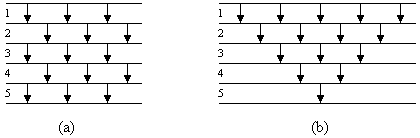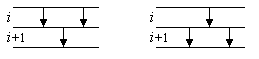SortiernetzeKorrektheit von Odd-even Transposition Sort | 
|
Außer mithilfe des 0-1-Prinzips lässt sich die Korrektheit von Odd-even-Transposition Sort auch in folgender Weise zeigen.
Idee
Es wird ein Verfahren angegeben, um das Odd-even-Transposition-Sortiernetz durch äquivalente Umformungen in ein Bubblesort-Netz zu überführen und umgekehrt. Da Bubblesort ein Sortiernetz ist, folgt dass auch Odd-even Transposition Sort ein Sortiernetz ist.
Bild 1 zeigt die Sortiernetze Odd-even-Transposition Sort und Bubblesort für Datenfolgen der Länge n = 6.
| |
| Bild 1: Odd-even Transposition Sort (a) und Bubblesort (b) für n = 6 | |
Grundlagen
Odd-even Transposition-Sort und Bubblesort sind primitive Vergleichernetze, d.h. Vergleiche finden nur zwischen benachbarten Datenelementen statt. In primitiven Vergleichernetzen notieren wir einen Vergleicher [i-1 : i] nur durch die Zahl i.
Das Vergleichernetz Odd-even Transposition Sort aus Bild 1a entspricht somit der Vergleicherfolge 1 3 5 2 4 1 3 5 2 4 1 3 5 2 4. Das Vergleichernetz Bubblesort aus Bild 1b entspricht der Vergleicherfolge 1 2 3 4 5 1 2 3 4 1 2 3 1 2 1.
Satz: Zwei Vergleicher i, j 
{1, ..., n-1} in einem primitiven Vergleichernetz sind unabhängig, wenn |i – j| > 1 ist.
Beispielsweise sind die ersten drei Vergleicher 1, 3, und 5 von Odd-even Transposition Sort jeweils unabhängig voneinander. Eine Menge von paarweise unabhängigen Vergleichern lässt sich in beliebiger Reihenfolge hintereinanderausführen (oder parallel ausführen), die entsprechenden Vergleichernetze sind äquivalent, d.h. bewirken dieselbe Abbildung.
In einem primitiven Vergleichernetz gilt daher für zwei Vergleicher i und j:
i j 
j i, falls |i – j| > 1
Durch derartige Vertauschungen von Vergleichern allein lässt sich Odd-even Transposition Sort noch nicht in Bubblesort überführen. Dies ist erst durch zusätzliche Anwendung der sogenannten Artin-Relation möglich, die wie folgt lautet:
i i+1 i i+1 i i+1
Die Relation drückt aus, dass die folgenden Vergleichernetze äquivalent sind. Tatsächlich ist dies der Fall, denn es handelt sich um Sortiernetze für n = 3.
| |
| Bild 2: Äquivalente Vergleichernetze i i+1 i und i+1 i i+1 | |
Umformung
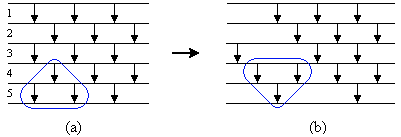
Durch eine Folge von erlaubten Vertauschungen von Vergleichern und Anwendungen der Artin-Relation lässt sich Odd-even Transposition Sort in Bubblesort überführen. Eine mögliche Strategie besteht darin, alle Vorkommen des Vergleichers n-1 durch mehrfache Anwendung der Relation n-1 n-2 n-1 n-2 n-1 n-2 auf ein einziges Vorkommen zu reduzieren, alle Vorkommen von n-2 auf zwei Vorkommen zu reduzieren usw. Bild 3 zeigt die erste entsprechende Anwendung der Artin-Relation.
| |
| Bild 3: Ersetzen von 5 4 5 durch 4 5 4 | |
Folgende Tabelle zeigt die Überführung eines Odd-even-Transposition-Sortiernetzes für n = 6 in ein Bubblesort-Netz durch Anwendung von Vertauschungen von Vergleichern (V) und Anwendungen der Artin-Relation (A).
| 1 | 3 | 5 | 2 | 4 | 1 | 3 | 5 | 2 | 4 | 1 | 3 | 5 | 2 | 4 | |
| V | 1 | 3 | 2 | 5 | 4 | 5 | 1 | 3 | 2 | 4 | 1 | 3 | 5 | 2 | 4 |
| A | 1 | 3 | 2 | 4 | 5 | 4 | 1 | 3 | 2 | 4 | 1 | 3 | 5 | 2 | 4 |
| V | 1 | 3 | 2 | 4 | 5 | 1 | 4 | 3 | 4 | 2 | 1 | 3 | 5 | 2 | 4 |
| A | 1 | 3 | 2 | 4 | 5 | 1 | 3 | 4 | 3 | 2 | 1 | 3 | 5 | 2 | 4 |
| V | 1 | 3 | 2 | 4 | 1 | 3 | 5 | 4 | 5 | 3 | 2 | 1 | 3 | 2 | 4 |
| A | 1 | 3 | 2 | 4 | 1 | 3 | 4 | 5 | 4 | 3 | 2 | 1 | 3 | 2 | 4 |
| V | 1 | 3 | 2 | 1 | 4 | 3 | 4 | 5 | 4 | 3 | 2 | 1 | 3 | 2 | 4 |
| A | 1 | 3 | 2 | 1 | 3 | 4 | 3 | 5 | 4 | 3 | 2 | 1 | 3 | 2 | 4 |
| V | 1 | 3 | 2 | 1 | 3 | 4 | 3 | 5 | 4 | 3 | 2 | 3 | 1 | 2 | 4 |
| A | 1 | 3 | 2 | 1 | 3 | 4 | 3 | 5 | 4 | 2 | 3 | 2 | 1 | 2 | 4 |
| V | 1 | 3 | 2 | 1 | 3 | 4 | 3 | 5 | 2 | 4 | 3 | 4 | 2 | 1 | 2 |
| A | 1 | 3 | 2 | 1 | 3 | 4 | 3 | 5 | 2 | 3 | 4 | 3 | 2 | 1 | 2 |
| V | 1 | 3 | 2 | 3 | 1 | 4 | 3 | 5 | 2 | 3 | 4 | 3 | 2 | 1 | 2 |
| A | 1 | 2 | 3 | 2 | 1 | 4 | 3 | 5 | 2 | 3 | 4 | 3 | 2 | 1 | 2 |
| V | 1 | 2 | 3 | 4 | 5 | 2 | 1 | 3 | 2 | 3 | 4 | 3 | 2 | 1 | 2 |
| A | 1 | 2 | 3 | 4 | 5 | 2 | 1 | 2 | 3 | 2 | 4 | 3 | 2 | 1 | 2 |
| V | 1 | 2 | 3 | 4 | 5 | 2 | 1 | 2 | 3 | 4 | 2 | 3 | 2 | 1 | 2 |
| A | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 1 | 3 | 4 | 2 | 3 | 2 | 1 | 2 |
| V | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 2 | 1 | 2 |
| A | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 1 | 2 | 1 |
 |
 H.W. Lang Hochschule Flensburg lang@hs-flensburg.de Impressum Datenschutz © Created: 21.2.2004 Updated: 04.06.2018 |
 |
