Travelling-Salesman-Problem
Heuristische Verfahren
Problem
Das
Es gibt (n-1)! Möglichkeiten, beginnend bei einer bestimmten Stadt alle anderen Städte zu besuchen und wieder zur Ausgangsstadt zurückzukehren, zuviele, um alle durchzuprobieren. Ein schnelleres Verfahren, das weniger als exponentielle Zeit benötigt, ist nicht bekannt und existiert wahrscheinlich auch nicht, denn
Es stellt sich daher die Frage nach approximativen Verfahren, die zwar nicht unbedingt die beste Lösung finden, aber dieser sehr nahekommen. Hier sollen die Verfahren Simulated Annealing und Selbstorganisierende Karte [RMS 90] angewendet werden, um das
Approximative Optimierungsverfahren versuchen meist, ausgehend von einer vorhandenen Lösung durch eine geeignete Abänderung zu einer besseren Lösung zu gelangen. Führt keine solche mögliche Abänderung mehr zu einer Verbesserung, so ist ein Optimum gefunden. Das Problem hierbei ist, dass es sich um ein lokales Optimum handeln kann, das wesentlich schlechter ist als das globale Optimum.
Bild 1 zeigt diese Situation am Beispiel eines Minimierungsverfahrens. Die Ausgangslösung ist A, durch schrittweise Verbesserung ist das Verfahren zur Lösung B gelangt. Alle Schritte, die von B aus möglich sind, führen zu einer Verschlechterung der Lösung, B ist ein lokales Minimum. Das globale Minimum liegt jedoch bei D. Das Verfahren kann das globale Minimum jetzt nur noch finden, wenn es für eine begrenzte Anzahl von Schritten auch eine Verschlechterung der Lösung in Kauf nimmt, sodass es über den Berg C gelangen kann (Bild 1).
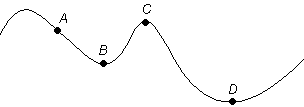
Bild 1: Lokales und globales Minimum
Die beiden hier vorgestellten Verfahren haben diese Eigenschaft, dass sie zwar einerseits die Lösung zu verbessern versuchen, andererseits aber auch Verschlechterungen um nicht mehr als sigma akzeptieren. Der Parameter sigma wird im Verlauf des Verfahrens kontinuierlich verringert, bis schließlich überhaupt keine Verschlechterungen mehr zugelassen werden.
Simulated Annealing
Der Begriff Annealing stammt aus der Metallurgie und bezeichnet das Tempern von Metallen. Ein Metall ist umso härter, je besser sich eine geordnete Kristallstruktur ausgebildet hat. Beim Erstarren aus der Schmelze bilden sich an vielen Stellen Kristallisationszentren, und das Ergebnis ist ein Metall, bei dem viele kleine Kristalle kreuz und quer durcheinanderliegen. Beim Tempern wird nun das Metall nochmals bis kurz vor den Schmelzpunkt erhitzt und dann langsam wieder abgekühlt, sodass sich die Kristallstruktur des Metalls besser ausbilden kann; es bilden sich größere Kristalle, da die Metallatome innerhalb der Kristallstruktur eine niedrigere potentielle Energie haben als außerhalb der Kristallstruktur.
Durch das Tempern wird den Metallatomen noch einmal die Möglichkeit gegeben, sich zu bewegen, sodass sie beim Abkühlen einen energetisch günstigeren Platz finden können. Das Tempern muss sehr vorsichtig geschehen: wird das Metall zu stark erhitzt, kommen alle Atome wieder durcheinander und die vorher schon gefundene Ordnung wird wieder zerstört. Wird es zu schwach erhitzt, lösen sich die Atome nicht aus ihrer alten Ordnung und es wird keine bessere Ordnung gefunden.
Indem dieser Prozess des Temperns zur Herstellung eines Zustandes möglichst niedriger Energie simuliert wird – daher die Bezeichnung Simulated Annealing – erhält man ein Optimierungsverfahren. Die Temperatur entspricht hierbei dem oben erwähnten Parameter sigma.
Anwendung auf das Travelling-Salesman -Problem
Um das
Die Reihenfolge der Städte in der neuen Rundreise ergibt sich aus der alten Reihenfolge wie folgt:
alte Reihenfolge: ... si-1 si si+1 ... sj-1 sj sj+1 ...
neue Reihenfolge: ... si-1 sj sj-1 ... si+1 si sj+1 ...
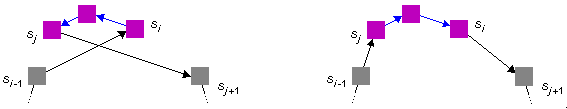
Bild 2: Ursprüngliche und verbesserte Lösung
Ist die neue Rundreise kürzer als die alte Rundreise, so wird mit dieser verbesserten Lösung fortgefahren. Ist sie länger, so wird sie nur dann akzeptiert, wenn sie um höchstens sigma länger ist als die alte Rundreise. Ansonsten wird sie verworfen, und es wird mit der alten Lösung fortgefahren.
Nach jeweils einer bestimmten Anzahl von Iterationsschritten wird der Parameter sigma verringert, bis er den Wert 0 erreicht, sodass zum Schluss keine Verschlechterung der Lösung mehr zugelassen wird.
Selbstorganisierende Karte
Gegeben ist ein Raum (S, d) von Stimuli; d ist eine Metrik auf S. Ferner ist ein Raum (N, g) von Neuronen gegeben; g ist eine Metrik auf N. Ziel ist es, eine Zuordnung z zwischen S und N zu finden, derart dass nah beieinander liegenden Stimuli auch nah beieinander liegende Neuronen zugeordnet sind, also eine Art stetige Abbildung.
Anwendung auf das Travelling-Salesman -Problem
Die Menge der Stimuli S ist eine endliche Menge von Punkten in der Ebene (die Städte des
Bild 3 veranschaulicht diese Situation: Die Stimuli sind rot eingezeichnet. Die blauen Punkte sind die Neuronen, und zwar ist jedes Neuron n ∈ N an der Position p(n) eingezeichnet. Außerdem sind die Kanten zwischen den Neuronen im Graphen G eingezeichnet. Weiterhin ist eine Abbildung z eingezeichnet, und zwar ist jedem Stimulus das nächstgelegene Neuron zugeordnet.
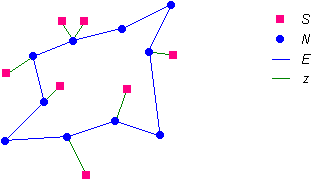
Bild 3: Stimuli S und Neuronen N
Die dargestellte Situation hat schon die gewünschte Eigenschaft, dass nah beieinander liegenden Stimuli auch einigermaßen nah beieinander liegende Neuronen zugeordnet sind. Die Situation lässt sich aber durch Adaptionsschritte noch verbessern.
Ein Adaptionsschritt besteht darin, dass ein Stimulus s zufällig gewählt wird. Daraufhin rückt das dem Stimulus s am nächsten liegende Neuron n um einen bestimmten Faktor h näher an s heran. Aber auch die beiden Neuronen, die im Graphen direkt mit n benachbart sind, rücken näher an s heran, allerdings um weniger als h. Und auch die Neuronen, die sich im Abstand g = 2, 3, ... von n befinden, rücken an s heran, jedoch umso weniger, je größer g ist.
Bild 4 zeigt, wie die Neuronen in einem Adaptionsschritt an den Stimulus s heranrücken.
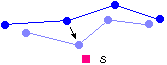
Bild 4: Adaptionsschritt
Begonnen wird mit einer beliebigen Verteilung der Neuronen in der Ebene, z.B. p(n) = (0,0) für alle n ∈ N. Durch eine Folge von Adaptionsschritten wird die Zuordnung z dann verbessert. Wie gut dies gelingt, hängt zum einen von der Anzahl der Neuronen ab und zum anderen davon, wie der Faktor h in Abhängigkeit vom Abstand g gewählt wird. Zu Anfang sollte der Einfluss einer Adaption auf weiter entfernte Neuronen größer sein und dann im Verlauf der Berechnung immer kleiner werden. Im Allgemeinen wird die Formel
h(g) = ε · e -g/sigma
verwendet. Der Parameter sigma steuert den Einfluss der Adaption auf entferntere Neuronen, er ist zunächst groß und wird dann im Verlauf der Berechnung verringert. Der Parameter ε bestimmt die Stärke der Adaption überhaupt.
Am Ende der Berechnung ist der Raum N in den Raum S eingebettet. Damit ist N eine "Karte" von S, die sich durch die Adaption selbst organisiert hat, daher die Bezeichnung "selbstorganisierende Karte". Eine Rundreise durch die Städte ergibt sich, indem die Städte nach z(s) geordnet werden. Es zeigt sich, dass die erzeugten Rundreisen recht kurz sind.
Literatur
[RMS 90] H. Ritter, T. Martinetz, K. Schulten: Neuronale Netze. Addison-Wesley (1990)
[Web 1] http://www.tsp.gatech.edu/games/tspOnePlayer.html Spiel: Wie gut sind Sie selbst als Handlungsreisender?
Weiter: [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 16.03.1999 Updated: 10.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden