Travelling-Salesman-Problem

Faktor-2-Annäherungsverfahren

Das metrische Travelling-Salesman-Problem ist ein Spezialfall des Travelling-Salesman-Problems. Für diesen Fall gibt es ein Annäherungs­verfahren, das in poly­nomieller Zeit eine Rundreise findet, die höchstens doppelt so lang ist wie die optimale Rundreise.

Metrisches Travelling-Salesman-Problem

Definition:  Sei G = (V, E) ein vollständig verbundener ungerichteter Graph und w : E → ℝ eine Kanten­gewichtung. Dann ist die Kanten­gewichtung w metrisch, wenn sie die folgende Eigen­schaften einer Metrik hat:

w(i, j) = 0 ⇔  i = j

w(i, j) = w(j, i)

w(i, j) + w(j, k) ≥ w(i, k)

Aus den drei Bedingungen folgt, dass alle Kanten­gewichte nichtnegativ sind. Die zweite Bedingung ist von sich aus erfüllt, da der Graph ungerichtet ist. Entscheidend ist die Gültigkeit der letzten Bedingung, der Dreiecks­ungleichung. Sie besagt, dass der direkte Weg zwischen zwei Knoten nie länger ist als ein Umweg über einen anderen Knoten.

Das Travelling-Salesman-Problem in einem Graphen mit metrischer Kanten­gewichtung heißt metrisches Travelling-Salesman-Problem.

Das metrische Travelling-Salesman-Problem kommt in der Praxis wahr­scheinlich am häufigsten vor, da meistens Situationen modelliert werden, in denen die Kanten­gewichte tatsächliche Entfernungen sind, d.h. Abstände in einem metrischen Raum.

Verfahren

Das folgende Verfahren berechnet eine Rundreise, die höchstens doppelt so lang ist wie die optimale Rundreise. Grundlage ist das Verfahren zur Berechnung eines minimalen Spannbaums, das eine Zeit­komplexität von O(n2) hat.

 

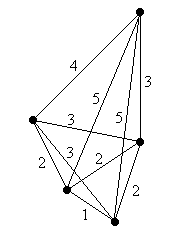
Ausgangs­punkt ist ein vollständig verbundener ungerichteter Graph G mit einer metrischen Kanten­gewichtung w.

 

G:
Ausgangsgraph G

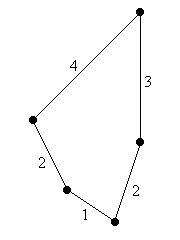
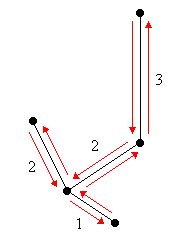
Sei K die (unbekannte) kürzeste Rundreise. In diesem Beispiel ist die Länge der kürzesten Rundreise

w(K) = 12.

 

K:
(Unbekannte) kürzeste Rundreise K

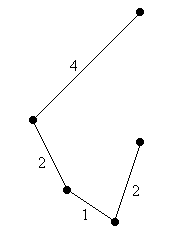
Wird eine Kante aus K entfernt, so entsteht ein Spannbaum S von G. Weil die Kante fehlt, gilt offenbar

w(S) ≤ w(K).

In diesem Beispiel ist w(S) = 9.

 

S:
Spannbaum S

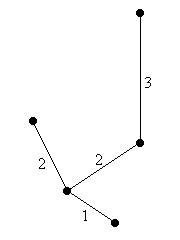
Mit dem Verfahren zur Berechnung eines minimalen Spannbaums wird ein minimaler Spannbaum M des Graphen G konstruiert. Da M minimal ist, gilt

w(M) ≤ w(S) ≤ w(K).

In diesem Beispiel ist w(M) = 8.

 

M:
Minimaler Spannbaum M

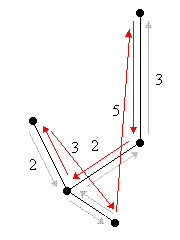
Sei nun D ein voller Durchlauf durch den minimalen Spannbaum M, d.h. ein Pfad, der bei einer Tiefensuche durch den Baum zustande kommt. Da jede Kante zweimal durchlaufen wird, gilt

w(D)  =  2w(M) ≤ 2w(S) ≤ 2w(K).

In diesem Beispiel ist w(D) = 16.

 

D:
Voller Durchlauf D durch M

Der volle Durchlauf D besucht manche Knoten mehrmals; in einer Rundreise soll aber jeder Knoten nur genau einmal besucht werden. Daher wird der volle Durchlauf D abgekürzt: Knoten, die schon besucht worden sind, werden übersprungen. Ausgenommen ist natürlich der Startknoten, dort endet der abgekürzte Durchlauf.

Das Ergebnis ist die gesuchte Rundreise R. Wegen der Dreiecks­ungleichung ist der abgekürzte Durchlauf R nicht länger als der volle Durchlauf D, d.h. es gilt

w(R) ≤ w(D)  =  2w(M) ≤ 2w(S) ≤ 2w(K).

Die Rundreise R ist also höchstens zweimal so lang wie die (unbekannte) kürzeste Rundreise K. In diesem Beispiel ist

w(R) = 15 ≤ 2 · 12.

 

R:
Abgekürzter Durchlauf R

Aufgaben

Aufgabe 1:  Gegeben seien n Punkte in der Ebene. Offenbar lässt sich hieraus ein metrisches Travelling-Salesman-Problem bilden, indem der euklidische Abstand zwischen den Punkten als Kanten­gewichtung genommen wird.

Zeigen Sie: Die kürzeste Rundreise ist planar. Oder anders ausgedrückt: Enthält eine Rundreise zwei sich über­kreuzende Kanten, so kann sie nicht die kürzeste Rundreise sein.

Aufgabe 2:  Geben Sie ein metrisches Travelling-Salesman-Problem mit 4 Knoten an, bei dem die Greedy-StrategieErklärung (gehe immer zum nächst­gelegenen Knoten) nicht die optimale Lösung liefert.

 

Weiter:  [Heuristische Verfahren]   oder   [up]

 

H.W. Lang   mail@hwlang.de   Impressum   Datenschutz
Created: 12.10.2005   Updated: 10.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden