NP-vollständige Probleme

Die Mengen P und NP

Im Bereich der Algorithmen entsprechen sich "schwierig" und "zeit­aufwendig". Ein Problem ist schwierig, wenn seine Lösung zeit­aufwendig ist. Der Begriff zeit­aufwendig ist natürlich relativ, aber es hat sich als sinnvoll erwiesen, hier eine Grenze zu ziehen zwischen Problemen mit höchstens poly­nomieller Zeit­komplexität und Problemen mit größerer als poly­nomieller Zeit­komplexität.

Die Menge P

Definition:  Eine Zeit­komplexität von T(n) ∈ O(nk) wird als polynomielle Zeit­komplexität bezeichnet. Hierbei ist k ein konstanter Wert, der nicht von n abhängt.

Definition:  Ein Problem hat polynomielle Zeit­komplexität, wenn es einen Algorithmus zur Lösung des Problems gibt, der polynomielle Zeit­komplexität hat.

Die Menge aller Ent­scheidungsprobleme, die polynomielle Komplexität haben, wird mit P bezeichnet.

Beispiel:  Sei G = (V, E) ein beliebiger ungerichteter, zusammen­hängender Graph mit einer Kanten­gewichtung w : E → ℕ sowie k eine beliebige Zahl.

Das Ent­scheidungsproblem "Hat G einen Spannbaum mit einem Gewicht  ≤ k?" liegt in P.

Wir konstruieren einen minimalen Spannbaum, dies erfordert Zeit O(n2), wobei n die Anzahl der Knoten des Graphen ist, und vergleichen das Gewicht des minimalen Spannbaums mit der Zahl k.

Nichtdeterministische Algorithmen

Das gedankliche Modell des Nicht­determinismus haben wir bei den endlichen Automaten kennen gelernt.

Ein nicht­deterministischer Algorithmus ist dadurch gekenn­zeichnet, dass er in jedem Schritt möglicherweise mehrere Wahl­möglichkeiten hat. Eine solche Wahl­möglichkeit könnte beispiels­weise darin bestehen, dass der Algorithmus frei wählen kann, ob er die Anweisung x=1, x=2 oder x=3 ausführt. Wohlgemerkt, er trifft seine Wahl nicht deterministisch etwa aufgrund einer Bedingung (wie bei einer If-Anweisung in einem deterministischen Algorithmus), sondern nicht­deterministisch. Je nach dem, welche Möglichkeit er wählt, gerät er aus seiner aktuellen Konfiguration in eine andere Folge­konfiguration. Eine solche Wahl­möglichkeit gibt es bei einem deterministischen Algorithmus nicht, die jeweilige Folge­konfiguration ist stets eindeutig bestimmt. Auch bei einer Verzweigung aufgrund einer Bedingung ist die Folge­konfiguration eindeutig, je nach dem, ob die Bedingung wahr oder falsch ist. Eine Berechnung eines deterministischen Algorithmus lässt sich durch eine Kette von Konfigurationen wie in Bild 1a ver­anschaulichen. Eine Berechnung eines nicht­deterministischen Algorithmus gleicht dagegen einem Baum von Konfigurationen wie in Bild 1b.

 

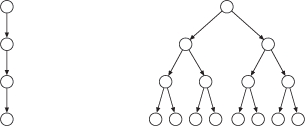
Bild 1: Deterministische Berechnung (a), nichtdeterministische Berechnung (b) 

Bild 1: Deterministische Berechnung (a), nichtdeterministische Berechnung (b)

 

Es ist schwierig, sich einen nicht­deterministischen Algorithmus vorzustellen. Welche Wahl trifft der Algorithmus, wenn er mehrere Wahl­möglichkeiten hat? Hier gibt es mehrere Möglich­keiten der Vorstellung: Eine ist, dass der Algorithmus mit schlaf­wandlerischer Sicherheit immer die richtige Wahl trifft, die zur Lösung des Problems führt. Die andere ist, dass er alle Wahl­möglichkeiten gleichzeitig durchspielt. Der Algorithmus erzeugt entsprechend viele Kopien von sich selbst, und jede dieser Kopien rechnet in der ent­sprechenden Folge­konfiguration weiter. Wenn irgendeine dieser Kopien die Lösung des Problems gefunden hat, stoppt der Algorithmus.

Die Menge NP

Definition:  Ein Problem hat nicht­deterministisch polynomielle Zeit­komplexität, wenn es einen nicht­deterministischen Algorithmus zur Lösung des Problems gibt, der polynomielle Zeit­komplexität hat.

Die Menge aller Ent­scheidungsprobleme, die nichtdeterministisch polynomielle Zeit­komplexität haben, wird mit NP bezeichnet.

Offenbar gilt P ⊆ NP, denn wenn es einen deterministischen poly­nomiellen Algorithmus zur Lösung eines Problems gibt, dann gibt es auch einen nicht­deterministischen poly­nomiellen Algorithmus zur Lösung des Problems, denn ein deterministischer Algorithmus lässt sich als Spezialfall eines nicht­deterministischen Algorithmus ansehen. Ob allerdings P eine echte Teilmenge von NP ist, weiß man nicht. Dies ist die bekannteste ungelöste Frage der Informatik.

Es sollen nun einige Probleme betrachtet werden, die in NP, aber wahr­scheinlich nicht P liegen.

Travelling-Salesman-Problem

Das Travelling-Salesman-Problem (TSP) liegt in NP. Als Ent­scheidungsproblem formuliert lautet es: "Gegeben n Städte und die Entfernungen zwischen ihnen. Gibt es eine Rundreise der Länge  ≤ k?" Die Länge einer Rundreise lässt sich deterministisch in linearer Zeit berechnen. Ein nicht­deterministischer Algorithmus verzweigt in jeder Stadt in alle Städte, die er noch nicht besucht hat, und spielt so alle Rundreisen durch.

Erfüll­barkeits­problem

Definition:  Das Erfüll­barkeits­problem (satisfiability problem – SAT) besteht darin, für eine beliebige boolesche Formel f mit Variablen x0, ..., xk-1 die Frage zu beantworten: "Ist f erfüllbar?" Eine boolesche Formel ist erfüllbar, wenn es eine Belegung ihrer Variablen mit den Wahrheits­werten true und false gibt, sodass die Auswertung der Formel den Wahrheits­wert true ergibt.

Beispiel:  Die Formel

f  =  (x0  ∨  x1)  ∧  (x0  ∨  x1)  ∧  (x0  ∨  x1)

ist erfüllbar, denn mit der Belegung x0 = true und x1 = false ergibt die Formel den Wert true.

Die Formel

g  =  x1  ∧  (x0  ∨  x1)  ∧  (x0  ∨  x1)

ist dagegen nicht erfüllbar.

Das Erfüll­barkeits­problem liegt in NP. Eine boolesche Formel der Länge n lässt sich deterministisch in linearer Zeit auswerten, wenn eine Belegung gegeben ist. Ein nicht­deterministischer Algorithmus verzweigt für jede Variable xj, auf die er bei der Auswertung trifft, in die beiden Möglich­keiten xj = true und xj = false und spielt dadurch alle Belegungen durch.

Cliquen-Problem

Definition:  Das Cliquen-Problem (CLIQUE) besteht darin, für einen beliebigen ungerichteten Graphen G mit n Knoten und für beliebiges k ∈ ℕ die Frage zu beantworten: "Enthält G eine k-Clique?" Eine k-Clique ist ein vollständig verbundener Teilgraph mit k Knoten.

Das Cliquen-Problem liegt in NP. Der nicht­deterministische Algorithmus verzweigt im ersten Schritt zu allen Knoten des Graphen. Von diesen Knoten aus verzweigt er zu allen benachbarten Knoten, von dort aus wiederum zu den benachbarten Knoten usw., insgesamt k-mal. In jedem Schritt prüft der Algorithmus (in poly­nomieller Zeit), ob der neue Knoten von allen bisher besuchten verschieden ist und mit diesen allen verbunden ist. Ist dies in allen k Schritten der Fall, so hat er eine k-Clique gefunden.

Hamilton­scher Kreis

Definition:  Gegeben ist ein ungerichteter Graph G = (V, E). Ein Hamilton­scher Kreis ist ein Kreis, der alle Knoten enthält, also ein Pfad, der jeden Knoten genau einmal durchläuft und zum Ausgangs­knoten zurückführt.

Das Problem des Hamilton­schen Kreises (Hamiltonian circuit – HC) besteht darin, für einen beliebigen ungerichteten Graphen G zu entscheiden, ob G einen Hamilton­schen Kreis enthält.

Das Problem des Hamilton­schen Kreises liegt in NP. Ein nicht­deterministischer Algorithmus zur Lösung von HC verzweigt an jedem Knoten zu allen benachbarten Knoten, die er noch nicht besucht hat, und sucht so alle Pfade durch den Graphen, die alle Knoten genau einmal enthalten und zum Ausgangs­knoten zurückführen.

 

Weiter mit:   [NP-Vollständigkeit]   oder [up]

 

H.W. Lang   mail@hwlang.de   Impressum   Datenschutz
Created: 25.05.2006   Updated: 10.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden