Mathematische Grundlagen
Verband
Verband
Definition: Eine Menge M mit zwei Verknüpfungen  und
und  ist ein Verband, wenn für alle a, b, c ∈ M folgende Bedingungen erfüllt sind:
ist ein Verband, wenn für alle a, b, c ∈ M folgende Bedingungen erfüllt sind:
(a  b) b)  c = a c = a  (b (b  c) c) | (Assoziativität) | |
(a  b) b)  c = a c = a  (b (b  c) c) | ||
a  b = b b = b  a a | (Kommutativität) | |
a  b = b b = b  a a | ||
a  (a (a  b) = a b) = a | (Absorption) | |
a  (a (a  b) = a b) = a |
Diese Bedingungen heißen Verbandsaxiome.
Satz: Sei G eine Menge und M = ℘(G) die Potenzmenge von G, d.h. die Menge aller Teilmengen von G. Dann bildet M mit den Verknüpfungen ∪ (Vereinigung) und ∩ (Durchschnitt) einen Verband, den Teilmengenverband von G.
Beweis: Um den Satz zu beweisen, müssen die Verbandsaxiome nachgerechnet werden. So ist z.B. als erstes zu zeigen, dass für alle Mengen A, B, C ∈ M gilt
(A ∪ B) ∪ C = A ∪ (B ∪ C)
Nach Definition der Vereinigung von Mengen ist
(A ∪ B) ∪ C = { x | (x ∈ A ∨ x ∈ B) ∨ x ∈ C }
Mithilfe einer Wahrheitstafel lässt sich zeigen, dass die logische Oder-Verknüpfung assoziativ ist:
(a ∨ b) ∨ c ⇔ a ∨ (b ∨ c) für alle a, b, c.
Damit ist
| (A ∪ B) ∪ C | = { x | (x ∈ A ∨ x ∈ B) ∨ x ∈ C } | |
| = { x | x ∈ A ∨ (x ∈ B ∨ x ∈ C) } | = A ∪ (B ∪ C) |
In ähnlicher Weise lässt sich auch zeigen, dass die anderen Verbandsaxiome gelten.
Satz: Sei k ∈ ℕ und Tk die Menge der positiven Teiler von k, also z.B. k = 24 und Tk = {1, 2, 3, 4, 6, 8, 12, 24}. Dann sind kgv (kleinstes gemeinsames Vielfaches ) und ggt (größter gemeinsamer Teiler) Verknüpfungen in Tk. Mit diesen Verknüpfungen bildet Tk einen Verband, den Teilerverband von k.
) und ggt (größter gemeinsamer Teiler) Verknüpfungen in Tk. Mit diesen Verknüpfungen bildet Tk einen Verband, den Teilerverband von k.
Beweis: Zunächst ist zu zeigen, dass die Verknüpfung ggt assoziativ ist, d.h. dass für alle a, b, c ∈ Tk gilt
ggt(ggt(a, b), c) = ggt(a, ggt(b, c))
Wir zeigen dies, indem wir nachweisen, dass die linke Seite die rechte Seite teilt und umgekehrt, also
ggt(ggt(a, b), c) | ggt(a, ggt(b, c)) und
ggt(a, ggt(b, c)) | ggt(ggt(a, b), c).
Sei d = ggt(ggt(a, b), c). Dann gilt nach Definition des größten gemeinsamen Teilers
d | ggt(a, b), also d | a und d | b, und d | c.
Dann aber gilt
d | ggt(b, c), denn d | b und d | c
und ferner
d | ggt(a, ggt(b, c)), denn d | a und d | ggt(b, c).
Damit ist bewiesen, dass die linke Seite die rechte Seite teilt. Die umgekehrte Richtung lässt sich genauso zeigen.
In ähnlicher Weise lässt sich auch die Assoziativität der Verknüpfung kgv zeigen.
Das dritte und vierte Verbandsaxiom fordert die Kommutativität von kgv und ggt. Offensichtlich sind kgv und ggt kommutativ.
Schließlich sind noch die Absorptionsgesetze zu beweisen. Dies ist Gegenstand der folgenden Aufgabe.
Aufgabe 1: Zeigen Sie die Gültigkeit des Absorptionsgesetzes
ggt(a, kgv(a, b)) = a,
indem Sie nachweisen, dass die linke Seite die rechte Seite teilt und umgekehrt. 
Zeigen Sie auf dieselbe Weise die Gültigkeit des anderen Absorptionsgesetzes
kgv(a, ggt(a, b)) = a.
Satz: Sei (M,  ,
,  ) ein Verband. Dann gilt für alle a ∈ M:
) ein Verband. Dann gilt für alle a ∈ M:
a  a = a a = a | (Idempotenz) | |
a  a = a a = a |
Der Beweis ist Gegenstand der folgenden Aufgabe.
Boolescher Verband
Definition: Ein Verband ist ein distributiver Verband, wenn die beiden Distributivgesetze gelten:
a  (b
(b  c) = (a
c) = (a  b)
b)  (a
(a  c) und
c) und
a  (b
(b  c) = (a
c) = (a  b)
b)  (a
(a  c)
c)
Beispiel: Sei G eine Menge. Dann ist der Teilmengenverband von G ein distributiver Verband.
Definition: Sei (M,  ,
,  ) ein Verband. Ein Element n ∈ M heißt Nullelement, wenn es bezüglich der Verknüpfung
) ein Verband. Ein Element n ∈ M heißt Nullelement, wenn es bezüglich der Verknüpfung  neutral ist, d.h. wenn gilt
neutral ist, d.h. wenn gilt
a  n = a für alle a ∈ M.
n = a für alle a ∈ M.
Ein Element e ∈ M heißt Einselement, wenn es bezüglich der Verknüpfung  neutral ist, d.h. wenn gilt
neutral ist, d.h. wenn gilt
a  e = a für alle a ∈ M.
e = a für alle a ∈ M.
Beispiel: Sei G eine Menge und M = ℘(G) der Teilmengenverband von G. Dann ist die leere Menge ∅ das neutrale Element bezüglich der Verknüpfung ∪ , denn es gilt für alle Mengen A ∈ ℘(G)
A ∪ ∅ = A.
Die Grundmenge G ist das neutrale Element bezüglich der Verknüpfung ∩ . Jede Menge A ∈ ℘(G) ist ja Teilmenge von G, und daher gilt
A ∩ G = A.
Aufgabe 3: Sei (M,  ,
,  ) ein Verband mit Nullelement n und Einselement e. Zeigen Sie, dass Nullelement und Einselement jeweils eindeutig bestimmt sind (zeigen Sie, indem Sie die Definition des Null- bzw. Einselementes heranziehen: wenn m und n Nullelemente sind, folgt m = n, bzw. wenn d und e Einselemente sind, folgt d = e).
) ein Verband mit Nullelement n und Einselement e. Zeigen Sie, dass Nullelement und Einselement jeweils eindeutig bestimmt sind (zeigen Sie, indem Sie die Definition des Null- bzw. Einselementes heranziehen: wenn m und n Nullelemente sind, folgt m = n, bzw. wenn d und e Einselemente sind, folgt d = e). 
Aufgabe 4: Sei (M,  ,
,  ) ein Verband mit Nullelement n und Einselement e. Zeigen Sie mithilfe der Absorptionsgesetze, dass für alle a ∈ M gilt:
) ein Verband mit Nullelement n und Einselement e. Zeigen Sie mithilfe der Absorptionsgesetze, dass für alle a ∈ M gilt:
a  n = n und
n = n und
a  e = e.
e = e.
Aufgabe 5: Zeigen Sie, dass jeder endliche Verband ein Nullelement und ein Einselement hat.
Anleitung: Sei (M,  ,
,  ) ein Verband, wobei M = {a1, ..., am} eine endliche Menge ist. Zeigen Sie mit mithilfe der Absorptionsgesetze, dass
) ein Verband, wobei M = {a1, ..., am} eine endliche Menge ist. Zeigen Sie mit mithilfe der Absorptionsgesetze, dass
n = a1  . . .
. . .  am
am
das Nullelement ist, d.h. dass für jedes ai ∈ M gilt
ai  n = ai.
n = ai.
Führen Sie einen entsprechenden Nachweis für das Einselement.
Aufgabe 6: Sei k ∈ ℕ und Tk der Teilerverband von k. Welches Element von Tk ist das neutrale Element n der Verknüpfung kgv und welches Element ist das neutrale Element e der Verknüpfung ggt?
Definition: Sei (M,  ,
,  ) ein Verband mit Nullelement n und Einselement e. Zwei Elemente a und a' heißen komplementär zueinander, wenn folgendes gilt:
) ein Verband mit Nullelement n und Einselement e. Zwei Elemente a und a' heißen komplementär zueinander, wenn folgendes gilt:
a  a' = e und
a' = e und
a  a' = n
a' = n
Das Element a' ist das Komplement von a (und umgekehrt).
Wenn jedes Element von M ein Komplement hat, dann heißt der Verband M komplementär.
Beispiel: Sei G eine Menge. Dann ist der Teilmengenverband von G ein komplementärer Verband. Das Komplement einer jeweiligen Menge A ∈ ℘(G) ist die Menge G \ A = { x | x ∈ G ∧ x ∉ A}.
Bemerkung: Bisher haben wir eine Menge mit zwei Verknüpfungen, Assoziativität, Kommutativität, Distributivität, neutrale Elemente, und mit dem Komplement jetzt auch noch eine Art inverses Element. Die entstehende Struktur hat auf den ersten Blick große Ähnlichkeit mit einem Körper.
Tatsächlich jedoch ist das Komplement etwas anderes als ein inverses Element in einem Körper. Wird in einem Körper ein Element mit seinem inversen Element verknüpft, so kommt das neutrale Element bezüglich derselben Verknüpfung heraus. Wird dagegen in einem Verband ein Element mit seinem Komplement verknüpft, so kommt zwar auch ein neutrales Element heraus, aber das neutrale Element bezüglich der anderen Verknüpfung. Bild 1 zeigt schematisch diese Situation; die beiden Verknüpfungen sind einheitlich mit + und · bezeichnet, die neutralen Elemente mit 0 und 1.
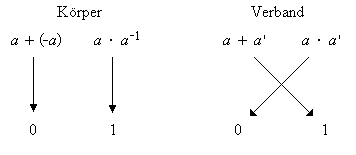
Bild 1: Unterschied zwischen inversen Elementen und Komplement
Definition: Ein distributiver, komplementärer Verband wird Boolescher Verband oder Boolesche Algebra genannt (nach G. Boole ).
).
Aufgabe 7: Zeigen Sie, dass der Teilerverband von 24 nicht komplementär ist und deshalb kein Boolescher Verband ist (zeigen Sie: es gibt ein Element in T24, das kein Komplement hat).
Aufgabe 8: Zeigen Sie, dass der Teilerverband von 42 komplementär ist (zeigen Sie: alle Elemente in T42 haben ein Komplement).
Halbordnung
In jedem Verband lässt sich vermittels der Verknüpfungen  und
und  eine Halbordnung
eine Halbordnung 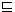 definieren.
definieren.
Definition: Sei (M,  ,
,  ) ein Verband. Auf M sei die Relation
) ein Verband. Auf M sei die Relation 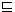 wie folgt definiert:
wie folgt definiert:
a 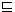 b ⇔ a
b ⇔ a  b = b für alle a, b ∈ M.
b = b für alle a, b ∈ M.
Behauptung: Die Relation 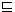 ist eine Halbordnung.
ist eine Halbordnung.
Aufgabe 9: Zeigen Sie, dass die Relation 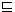 eine Halbordnung ist. Es ist zu zeigen, dass die Relation reflexiv, antisymmetrisch und transitiv ist, d.h. dass für alle a, b, c ∈ M gilt:
eine Halbordnung ist. Es ist zu zeigen, dass die Relation reflexiv, antisymmetrisch und transitiv ist, d.h. dass für alle a, b, c ∈ M gilt:
a 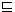 a
a
a 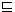 b ∧ b
b ∧ b 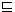 a ⇒ a = b
a ⇒ a = b
a 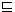 b ∧ b
b ∧ b 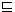 c ⇒ a
c ⇒ a 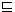 c
c
Aufgabe 10: Zeigen Sie unter Anwendung des Absorptionsgesetzes, dass folgendes gilt
Beispiel: Im Teilmengenverband einer Menge G ist die Relation ⊆ ("ist enthalten in", "ist Teilmenge von") die entsprechende Halbordnung; im Teilerverband einer Zahl k ist die Relation | ("teilt") die entsprechende Halbordnung.
Typisch für eine Halbordnung ist, dass im Allgemeinen nicht jedes Element mit jedem anderen vergleichbar ist (wie dies bei einer totalen Ordnung der Fall ist). So ist z.B im Teilmengenverband der Menge G = {1, 2, 3} die Menge {1, 2} weder eine Teilmenge von {2, 3}, noch umgekehrt. Im Teilerverband T24 ist 6 kein Teiler von 8, und umgekehrt auch nicht.
Hasse-Diagramm
Bei einem endlichen Verband M lässt sich mithilfe des Hasse-Diagramms veranschaulichen, welche Elemente miteinander vergleichbar sind.
Definition: Sei M eine endlicher Verband mit einer Halbordnung 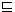 und sei
und sei 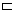 die zu
die zu 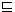 gehörige strenge Halbordnung. Das Hasse-Diagramm von M ist ein gerichteter Graph G = (M, E) mit der Knotenmenge M. Zwei Knoten u, w ∈ M werden durch eine Kante verbunden, wenn u
gehörige strenge Halbordnung. Das Hasse-Diagramm von M ist ein gerichteter Graph G = (M, E) mit der Knotenmenge M. Zwei Knoten u, w ∈ M werden durch eine Kante verbunden, wenn u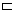 w gilt und es kein v ∈ M gibt mit u
w gilt und es kein v ∈ M gibt mit u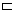 v
v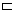 w.
w.
Beispiel: Der Teilerverband T24 = {1, 2, 3, 4, 6, 8, 12, 24} hat folgendes Hasse-Diagramm (Bild 2):
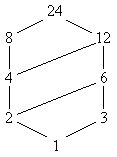
Bild 2: Hasse-Diagramm des Teilerverbandes T24
Die Knoten werden so angeordnet, dass die Kanten stets von unten nach oben gerichtet sind. Richtungspfeile an den Kanten können dann weggelassen werden.
Beispiel: Der Teilerverband T42 = {1, 2, 3, 7, 6, 14, 21, 42} hat folgendes Hasse-Diagramm (Bild 3):
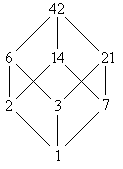
Bild 3: Hasse-Diagramm des Teilerverbandes T42
Weiter mit: [Matrix] [Literatur] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 14.08.2003 Updated: 10.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden