Grundlagen
Matrix
Definition
Definition: Sei K ein Körper. Eine m×n-Matrix über K ist eine Abbildung A : {1, ..., m} × {1, ..., n} → K.
Eine m × n-Matrix A wird in folgender Form geschrieben
| A = [ai,j] = | 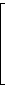 |
| 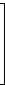 |
Die Matrix hat m Zeilen und n Spalten. Die Einträge der Matrix sind die Elemente ai,j ∈ K (i = 1, ..., m, j = 1, ..., n).
Die Schreibweise A = [ai,j] bedeutet, dass A eine Matrix ist, die aus den Einträgen ai,j mit i = 1, ..., m, j = 1, ..., n besteht. Hierbei müssen m und n aus dem Zusammenhang bekannt sein.
Die i-te Zeile von A ist der Zeilenvektor Ai,• , die j-te Spalte ist der Spaltenvektor A •, j . Man beachte die Stellung des Punktes im Index, an der zu erkennen ist, ob ein Zeilen- oder Spaltenvektor gemeint ist.
Ein Zeilenvektor lässt sich auch als 1×n-Matrix auffassen, ein Spaltenvektor als m×1-Matrix.
Beispiel: Folgende Matrix A ist eine 2×3-Matrix über ℝ :
| A = | 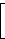 |
| 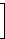 |
Die Zeilenvektoren von A sind A1,• = [ -1 2 -0 ] und A2,• = [ 0 3 -4 ], die Spaltenvektoren sind
| A •,1 = | 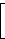 |
| 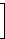 |
| A •,2 = | 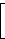 |
| 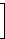 |
| A •,3 = | 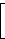 |
| 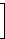 |
Matrixaddition
Um mit Matrizen rechnen zu können, definieren wir die Addition von Matrizen, die Multiplikation zwischen einem Element des Körpers K und einer Matrix und später auch die Multiplikation von Matrizen. Dabei wird auf die Rechenoperationen des zugrunde liegenden Körpers K zurückgegriffen.
Definition: Seien A und B zwei m×n-Matrizen. Die Addition geschieht komponentenweise:
[ai,j] + [bi,j] = [ai,j+bi,j]
Die Multiplikation einer Matrix A mit einem Element c ∈ K geschieht ebenfalls komponentenweise, d.h. indem jedes Matrixelement mit c multipliziert wird:
c·[ai,j] = [c·ai,j]
Beispiel:
| A = | 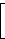 |
| 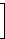 |
| A + A = | 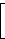 |
| 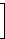 |
| 2·A = | 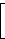 |
| 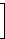 |
Definition:
Die Nullmatrix O ist die m×n-Matrix, deren Einträge alle 0 sind:
| O = |  |
|  |
Satz: Sei K ein Körper sowie m, n ∈ ℕ. Dann ist die Menge K(m,n) aller m×n-Matrizen über K ein Vektorraum über K.
Die Zahlen m und n müssen fest sein, da nur Matrizen gleicher Größe addiert werden können.
Matrixmultiplikation
Definition: Sei A eine m × n-Matrix und B eine n×p-Matrix. Das Produkt von A und B ist die m×p-Matrix C = [ci,j] mit
ci,j =  k=1, ..., n ai,k · bk,j
k=1, ..., n ai,k · bk,j
Jeder Eintrag ci,j ergibt sich also als Skalarprodukt des i-ten Zeilenvektors von A mit dem j-ten Spaltenvektor von B, d.h. es gilt
ci,j = Ai,• · B•, j
Bild 1 zeigt schematisch, wie das Element ci,j berechnet wird.
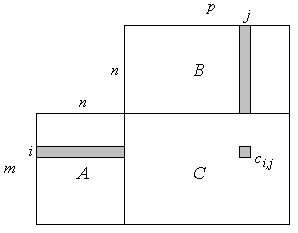
Bild 1: Berechnung eines Elements ci,j
Matrix-Vektor-Multiplikation
Die Multiplikation zwischen einer m×n-Matrix A und einem Spaltenvektor u der Länge n lässt sich auffassen als Matrixmultiplikation zwischen einer m×n- und einer n×1-Matrix. Das Ergebnis ist ein Spaltenvektor v der Länge m (Bild 2a).
Die Multiplikation zwischen einem Zeilenvektor u der Länge m und einer m×n-Matrix A und lässt sich auffassen als Matrixmultiplikation zwischen einer 1×m- und einer m×n-Matrix. Das Ergebnis ist ein Zeilenvektor v der Länge n (Bild 2b).
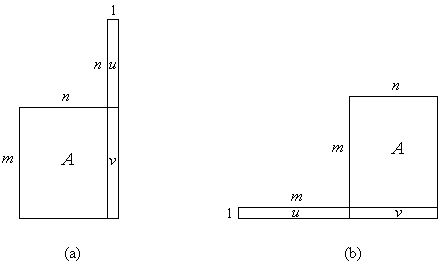
Bild 2: Matrix-Vektor-Multiplikation Au = v bzw. uA = v
Vektor-Vektor-Multiplikation
Die Multiplikation zwischen einem Zeilenvektor u der Länge n und einem Spaltenvektor v gleicher Länge lässt sich auffassen als Matrixmultiplikation zwischen einer 1×n- und einer n×1-Matrix. Das Ergebnis ist eine 1×1-Matrix bzw. ein Skalar s; die Berechnung entspricht der Bildung des Skalarprodukts (Bild 3a).
Die Multiplikation zwischen einem Spaltenvektor u der Länge m und einem Zeilenvektor v der Länge n lässt sich auffassen als Matrixmultiplikation zwischen einer m×1-Matrix und einer 1×n-Matrix. Das Ergebnis ist eine m×n-Matrix A (Bild 3b).
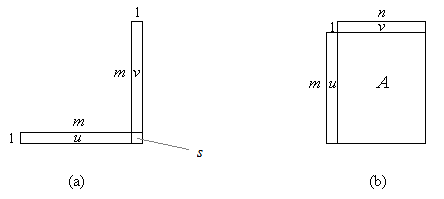
Bild 3: Vektor-Vektor-Multiplikation
Gelegentlich wird auch eine komponentenweise Multiplikation von Vektoren gleicher Länge benötigt. Diese wird mit dem Zeichen ⊙ notiert.
Beispiel: Es ist
[1 2 3] ⊙ [2 3 4] = [2 6 12]
Transposition
Definition: Sei A = [ai,j] eine m×n-Matrix. Die n×m-Matrix B mit
[bi,j] = [aj,i]
wird als die Transponierte AT von A bezeichnet; d.h. AT entsteht aus A, indem die Zeilen von A zu den Spalten von AT gemacht werden.
Beispiel:
| A = | 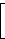 |
| 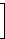 |
| AT = | 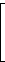 |
| 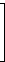 |
Aus einem Zeilenvektor wird durch Transposition ein Spaltenvektor und umgekehrt.
Quadratische Matrizen
Definition: Eine n×n-Matrix wird als quadratische Matrix bezeichnet. Eine quadratische Matrix A heißt symmetrisch, wenn A = AT gilt. Die Elemente ai,i einer quadratischen Matrix heißen Diagonalelemente. Eine quadratische Matrix heißt Diagonalmatrix, wenn alle Elemente außer möglicherweise den Diagonalelementen gleich 0 sind. Eine Diagonalmatrix heißt Einheitsmatrix, wenn alle Diagonalelemente gleich 1 sind.
Beispiel: Es seien
| A = | 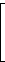 |
| 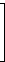 |
| D = | 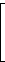 |
| 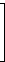 |
| I = | 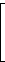 |
| 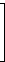 |
Alle Matrizen sind quadratisch, A ist symmetrisch, D ist Diagonalmatrix, I ist Einheitsmatrix.
Weiter mit: [Polynom] [Literatur] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 22.08.2000 Updated: 11.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden
