Graphenalgorithmen
Breitensuche in einem Graphen
Gegeben ist ein Labyrinth, etwa wie in Bild 1 dargestellt. Das Labyrinth hat ein Eingangsfeld und ein von dort erreichbares Ausgangsfeld; gesucht ist ein Weg vom Eingang des Labyrinths bis zum Ausgang.
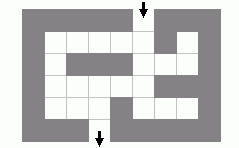
Bild 1: Labyrinth mit Eingang und Ausgang
Algorithmus
Der folgende Algorithmus berechnet die kürzesten Wege, gemessen in Anzahl der durchlaufenen Felder, vom Eingangsfeld zu allen anderen Feldern des Labyrinths und damit auch zum Ausgangsfeld.
Algorithmus Kürzester Weg durch ein Labyrinth
Eingabe:
Ein Labyrinth wie in Bild 1 dargestellt
Ausgabe:
Kürzester Weg vom Eingang des Labyrinths bis zum Ausgang
Methode:
- setze i = 0
- für jedes mit der Zahl i markierte Feld f wiederhole
- verbinde f mit allen noch nicht markierten Nachbarfeldern und markiere diese mit i+1
markiere das Eingangsfeld mit der Zahl 0
solange nicht alle Felder markiert sind wiederhole
setze i = i+1
gib die Folge der Felder entlang der Verbindungen vom Ausgang zum Eingang in umgekehrter Reihenfolge aus
Bild 2 zeigt die Markierungen der Felder und die auf diese Weise berechneten Verbindungen zwischen den Feldern.
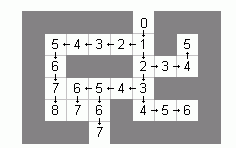
Bild 2: Kürzester Weg durch das Labyrinth
Bemerkung: Dieses Verfahren setzt voraus, dass wir globalen Überblick über das Labyrinth haben, dass wir quasi von oben auf das Labyrinth schauen. Wir haben also Zugriff auf jedes mit der Zahl i markierte Feld. Wenn wir uns in einer realen Situation auf einem bestimmten Feld eines Labyrinths befinden, sehen wir immer nur die unmittelbar benachbarten Felder. Dann ist ein anderes Verfahren erforderlich.
Modellierung
Wir modellieren das Problem durch einen ungerichteten Graphen. Die Knoten des Graphen entsprechen den Feldern des Labyrinths; zwei Knoten sind durch eine Kante verbunden, wenn die entsprechenden Felder benachbart sind. Bild 3a zeigt den entsprechenden Graphen für das Labyrinth aus Bild 1. Der Kürzeste-Wege-Algorithmus entspricht einer Breitensuche (engl.: breadth-first search) in dem zugehörigen Graphen. Die erzeugten Wege bilden einen Baum mit dem Startknoten als Wurzel, einen Breitensuchbaum (Bild 3b).
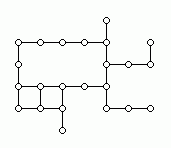
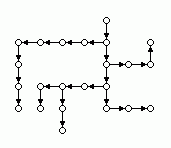
Bild 3: Modellierung des Labyrinths durch einen ungerichteten Graphen (a), Breitensuchbaum (b)
Der Algorithmus verwendet die Datenstruktur einer Schlange (Queue), um zu gewährleisten, dass die Knoten in der richtigen Reihenfolge, also breadth-first, besucht werden.
Zu jedem Knoten v bedeuten distance(v) die bisher gefundene kürzeste Entfernung zum Startknoten und predecessor(v) den zugehörigen Vorgänger im Baum. Auf diese Weise lässt sich der gesamte Breitensuchbaum darstellen.
Algorithmus Breitensuche
Eingabe:
Zusammenhängender ungerichteter Graph G = (V, E) mit V = {0, ..., n-1}, Startknoten s
Ausgabe:
Kürzeste Wege vom Startknoten s zu allen Knoten
Methode:
- setze distance(s) = 0
- entnimm den vordersten Knoten u aus der Schlange
- wenn v noch nicht als besucht markiert ist dann
- setze distance(v) = distance(u)+1
setze predecessor(s) = -1
markiere s als besucht
hänge Knoten s an die Schlange an
solange die Schlange nicht leer ist wiederhole
für alle Nachbarknoten v von u wiederhole
setze predecessor(v) = u
markiere v als besucht
hänge Knoten v an die Schlange an
Der Weg von einem bestimmten Knoten v zurück zum Startknoten s lässt sich anhand der Vorgänger zurückverfolgen.
Implementierung
Die folgende Klasse BreadthFirstTree berechnet die kürzesten Wege in einem Graphen vom Startknoten s zu allen anderen Knoten, sofern diese vom Startknoten aus erreichbar sind. Die Klasse basiert auf einer Klasse RootedTree, in der alle Daten und Methoden zum Aufbau des Breitensuchbaums zur Verfügung stehen. Mit den Methoden toTree und inTree wird Buch darüber geführt, welche Knoten schon besucht worden sind, d.h. schon zum bisher berechneten Baum der kürzesten Wege dazugehören.
Für das Durchlaufen aller Nachbarn eines Knotens wird ein NeighbourIterator verwendet.
{
private Graph<?> graph; // Graph (ohne Kantengewichtung)
public BreadthFirstTree(Graph<?> graph, int s)
{
super(graph.getSize());
this.graph=graph;
computeBreadthFirstTree(s);
}
// führt den Algorithmus Breitensuche aus
private void computeBreadthFirstTree(int s)
{
int u, v;
Iterator<Integer> it;
Queue<Integer> queue=new Queue<Integer>();
setDistance(s, 0);
setPredecessor(s, -1);
toTree(s);
queue.insert(s);
while (!queue.isEmpty())
{
u=queue.extract();
it=graph.getNeighbourIterator(u);
while (it.hasNext())
{
v=it.next();
if (!inTree(v))
{
setDistance(v, getDistance(u)+1);
setPredecessor(v, u);
toTree(v);
queue.insert(v);
}
}
}
}
// true, wenn Knoten v vom Startknoten aus erreichbar ist
public boolean isReachable(int v)
{
return hasPredecessor(v);
}
} // end class BreadthFirstTree
Mit der Anweisung
werden die kürzesten Wege in einem Graphen g von einem Startkonten s zu allen anderen Knoten berechnet. Mit den Methoden getDistance und getPredecessor kann anschließend für jeden Knoten die Entfernung zum Startknoten und der jeweilige Vorgänger im Baum ermittelt werden. Die Methode getPathTo liefert die Folge der Knoten vom Startknoten s zu einem Knoten v.
Die im Algorithmus verwendete Queue lässt sich auf Basis einer LinkedList implementieren.
Zusammenfassung
Wir haben ein konkretes Problem als graphentheoretisches Problem modelliert.
Mit dem Verfahren Breitensuche (breadth-first search) lassen sich die kürzesten Wege in einem Graphen bestimmen. Die Länge eines Weges bemisst sich dabei nach der Anzahl der durchlaufenen Kanten, d.h. jeder Kante wird die Länge 1 zugeordnet.
Häufig werden Probleme durch Graphen modelliert, deren Kanten selbst bereits mit bestimmten Längen oder Gewichten markiert sind. Um die kürzesten Wege in einem Graphen mit Kantengewichtung zu finden, ist das Verfahren Kürzeste Wege geeignet.
Wie bereits bemerkt, ist Breitensuche nicht möglich, wenn wir uns real in einem Labyrinth befinden, weil wir dann immer nur Zugriff auf die direkten Nachbarfelder desjenigen Feldes haben, auf dem wir uns gerade befinden. In diesem Fall lässt sich das Verfahren Tiefensuche (depth-first search) anwenden; allerdings findet es nicht unbedingt den kürzesten Weg. Tiefensuche in einem realen Labyrinth angewandt geht so: Wir tasten uns immer an der rechten Wand entlang, dann kommen wir irgendwann zu einem Ausgang.
Weiter mit: [Zusammenhangskomponenten eines Graphen] [Literatur] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 25.10.2006 Updated: 20.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden