Graphenalgorithmen

Maximaler Fluss

Gegeben ist ein Netzwerk mit einer Quelle (source) s und einer Senke (target) t (Bild 1). Gesucht ist ein maximaler Fluss von der Quelle s zur Senke t entlang der Verbindungen des Netzwerkes, unter Beachtung der Durchflusskapazitäten der einzelnen Verbindungen, die als Zahlenwerte angegeben sind.

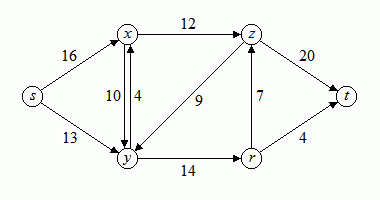
Bild 1: Netzwerk

Das obige Netzwerk kann beispielsweise einen Fluss mit dem Wert 10 auf dem Weg über die Knoten s-x-z-t aufnehmen. Hierdurch werden die Durchflusskapazitäten der durchlaufenen Verbindungen zwar nicht ausgeschöpft, aber jedenfalls auch nicht überschritten. Bild 2 zeigt diesen Fluss, dargestellt als erste Zahl, getrennt durch einen senkrechten Strich von der Durchflusskapazität. Ist nur eine Zahl angegeben, so handelt es sich um die Durchflusskapazität und der Fluss beträgt 0.

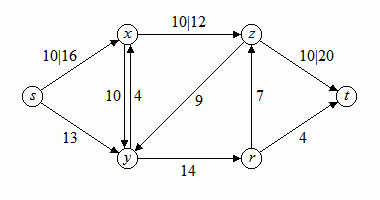
Bild 2: Netzwerk mit Fluss (erste Zahl Fluss, zweite Zahl Kapazität der Kante)

Dieser Fluss ist jedoch nicht maximal – wir können ihn sogar auf den Wert 12 steigern. Zusätzlich können wir ihn ergänzen um einen weiteren (Teil-)Fluss mit dem Wert 11, den wir auf dem Weg s-y-r auf die Reise schicken. Dieser Fluss spaltet sich am Knoten r dann auf. Ein Teil vereinigt sich am Knoten z mit dem erstgenannten Fluss, der von dort aus nun den Wert 12 + 7 = 19 hat. Die Durchflusskapazität der Verbindung z-t wird hierdurch nicht überschritten.

Das folgende Bild 3 zeigt diesen Fluss, wiederum dargestellt als erste Zahl, getrennt durch einen senkrechten Strich von der Durchflusskapazität.

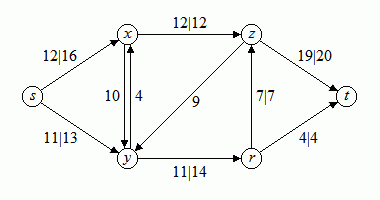
Bild 3: Netzwerk mit Fluss (erste Zahl Fluss, zweite Zahl Kapazität der Kante)

Es stellt sich die Frage, ob dieser Fluss maximal ist, oder ob er sich noch auf einen größeren Wert steigern lässt. Die Regeln hierbei sind: Die Durchflusskapazitäten der Verbindungen dürfen nicht überschritten werden, und alles was in einen Knoten hineinfließt, fließt auch wieder hinaus (abgesehen von der Quelle s und der Senke t).

Wir modellieren das Problem mithilfe eines gerichteten Graphen mit Kantenmarkierung. Statt von Verbindungen zwischen den Knoten des Netzwerks sprechen wir nun von Kanten des Graphen.

Definition: Ein Flussnetzwerk (flow network) ist ein gerichteter Graph G = (V, E, c) mit Knotenmenge V, Kantenmenge E und nichtnegativer Kantenmarkierung c : E → ℝ. Das Flussnetzwerk hat zwei ausgezeichnete Knoten s mit Eingangsgrad 0 und t mit Ausgangsgrad 0. Die anderen Knoten nennen wir die inneren Knoten des Netzwerks.

Die Knoten s und t spielen eine spezielle Rolle als Quelle (source) s und als Senke (target) t eines Flusses durch das Netzwerk. Eine Kantenmarkierung c wird interpretiert als Kapazität (capacity), d.h. als maximale Durchflussmenge der betreffenden Kante.

Fluss

Definition: Sei G = (V, E, c) ein Flussnetzwerk. Ein Fluss (flow) in dem Netzwerk ist eine Abbildung f : E → ℝ mit folgenden beiden Eigenschaften:

f(e) ≤ c(e) für alle Kanten e ∈ E,

Summe _{(u, v) ∈ E} f(u, v) = Summe _{(v, w) ∈ E} f(v, w) für alle inneren Knoten v, also für alle Knoten v ∈ V \ {s, t}.

Die beiden Eigenschaften bedeuten, dass der Fluss f(e) durch eine Kante e durch ihre Kapazität c(e) begrenzt ist und dass genau das, was in einen inneren Knoten v hineinfließt auch wieder herausfließt.

Das folgende Bild zeigt einen möglichen Fluss durch das obige Netzwerk; jede Kante e ist mit f(e) | c(e) beschriftet, d.h. die erste Zahl stellt den Fluss durch die Kante dar, die zweite Zahl die Kapazität der Kante, also ihre maximale Durchflussmenge.

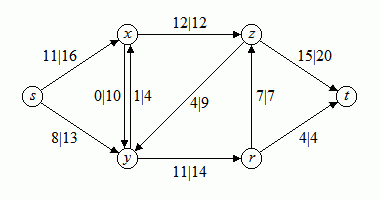
Bild 4: Fluss in einem Netzwerk (erste Zahl Fluss, zweite Zahl Kapazität der Kante)

Definition: Der Wert | f | eines Flusses f in einem Netzwerk ist der Gesamtfluss, der aus der Quelle s entspringt:

| f | = Summe _{(s,v) ∈ E} f(s, v)

Beispielsweise hat der Fluss in dem Netzwerk in Bild 4 den Wert 19. Wegen der zweiten Eigenschaft eines Flusses, nämlich dass aus allen inneren Knoten genauso viel wieder herausfließt wie hineinfließt, ist dieser Wert gleich dem Wert des Flusses, der in die Senke hineinfließt.

Wenn ein Fluss durch ein Netzwerk gegeben ist, so stellt sich die Frage, ob dieser Fluss noch gesteigert werden kann. Im einleitenden Absatz hatten wir gesehen, dass ein Fluss mit dem Wert 10 noch auf den Wert 12 gesteigert werden konnte, und dass ein zusätzlicher (Teil-)Fluss hinzugenommen werden konnte, wodurch der Gesamtfluss noch einmal gesteigert wurde.

Wir suchen also nach Wegen von der Quelle s zur Senke t, auf denen der Fluss die maximale Durchflusskapazität noch nicht ausschöpft, oder auf denen ein Fluss quasi in die falsche Richtung fließt. Einen derartigen Weg nennen wir einen Steigerungsweg (augmentation path). Ein Steigerungsweg bietet die Möglichkeit, den Gesamtfluss noch zu steigern.

Die möglichen Steigerungswege sind genau die Wege von der Quelle s zur Senke t in einem im Folgenden definierten Restkapazitäten-Netzwerk.

Definition: Gegeben ist ein Flussnetzwerk G = (V, E, c) mit einem Fluss f. Wir bilden hierzu ein weiteres Flussnetzwerk G' = (V, E', c'), das wir als Restkapazitäten-Netzwerk (residual network) bezeichnen.

Das Netzwerk G' hat dieselbe Knotenmenge V wie G. Die Kantenmenge E' besteht aus

allen Kanten e ∈ E mit f(e) < c(e), also allen Kanten, deren Kapazität durch den Fluss f nicht ausgeschöpft wird; diese Kanten heißen Vorwärtskanten,
allen Kanten e^-1 (also in umgekehrter Richtung) mit e ∈ E, für die f(e) > 0 gilt; diese Kanten heißen Rückwärtskanten.

Die Kapazität einer Vorwärtskante e beträgt c'(e) = c(e) – f(e); die Kapazität einer Rückwärtskante e^-1 beträgt c'(e^-1) = f(e).

Ein Steigerungsweg ist ein Weg im Restkapazitäten-Netzwerk von der Quelle s zur Senke t.

Das folgende Bild 5 zeigt das Restkapazitäten-Netzwerk zu dem Netzwerk mit dem dort eingezeichneten Fluss aus Bild 4.

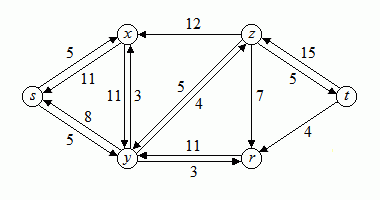
Bild 5: Restkapazitäten-Netzwerk

Ein Weg von der Quelle s zur Senke t in diesem Restkapazitäten-Netzwerk ist beispielsweise der Weg über die Knoten s-x-y-z-t. Dieser Weg stellt somit einen Steigerungsweg für das ursprüngliche Netzwerk dar. Der Wert, um den sich der Gesamtfluss im ursprünglichen Netzwerk steigern lässt, ergibt sich als das Minimum der Kapazitäten der Kanten des Wegs im Restkapazitäten-Netzwerk. In diesem Beispiel ist dieser Wert 4. Indem der Fluss entlang dieses Weges im ursprünglichen Netzwerk um 4 gesteigert wird, ergibt sich der folgende in Bild 6 dargestellte Fluss in dem Netzwerk.

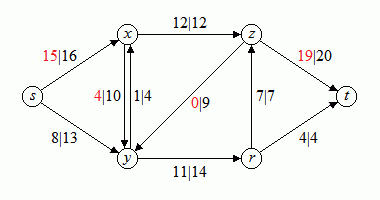
Bild 6: Netzwerk mit gesteigertem Fluss

Zur Berechnung eines möglichen Steigerungswegs suchen wir in dem Restkapazitäten-Netzwerk einen Weg von der Quelle s zur Senke t mithilfe der Breitensuche. Wir steigern dann den Fluss entsprechend und passen das Restkapazitäten-Netzwerk entsprechend an. Anschließend suchen wir einen weiteren Weg – solange, bis es keinen Weg mehr gibt. Wir beginnen mit dem ursprünglichen Netzwerk, das einem Restkapazitäten-Netzwerk mit einem Fluss mit Wert 0 entspricht.

Dieses Vorgehen ist in der Funktion computeMaxFlow im unten angegebenen Programm realisiert.

Um eine obere Schranke für den maximalen Fluss durch ein Netzwerk zu gewinnen, betrachten wir Schnitte durch das Netzwerk.

Definition: Sei G = (V, E, c) ein Flussnetzwerk mit Quelle s und Senke t. Ein Schnitt (S, T) durch das Netzwerk ist eine Partition der Knotenmenge V in zwei Mengen S mit s ∈ S und T mit t ∈ T.

Die Kapazität c(S, T) des Schnittes ist definiert als die Summe der Kapazitäten der Kanten, die von S nach T verlaufen:

c(S, T) = Summe _{u ∈ S, v ∈ T} c(u, v)

Etwas anders ist der Fluss des Schnitts definiert; vom Fluss durch die Kanten, die von S nach T führen, wird der Fluss durch die Kanten, die von T nach S wieder zurückführen, abgezogen:

f(S, T) = Summe _{u ∈ S, v ∈ T} f(u, v) – Summe _{u ∈ T, v ∈ S} f(u, v)

Das folgende Bild 7a zeigt einen Schnitt (S, T) durch das Netzwerk aus Bild 4. Die Teilmenge S besteht aus den Knoten s, x, y, z und die Teilmenge T aus den Knoten r, t. Bild 7b zeigt einen trivialen Schnitt: Die Teilmenge S besteht nur aus dem Knoten s, die Teilmenge T aus allen anderen Knoten.

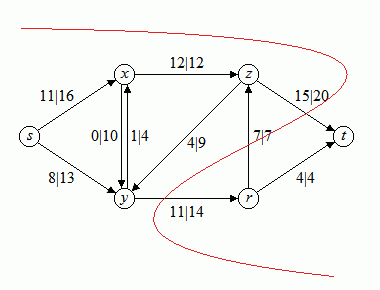
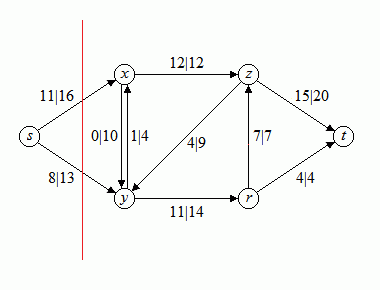
yes Bild 7: Schnitt durch ein Netzwerk (a), trivialer Schnitt (b)

Bild 7: Schnitt durch ein Netzwerk (a), trivialer Schnitt (b)

Die Kapazität des Schnitts aus Bild 7a beträgt 20 + 14 = 34, der Fluss des Schnitts beträgt 15 - 7 + 11 = 19. Die Kapazität des Schnitts aus Bild 7b beträgt 16 + 13 = 29, der Fluss des Schnitts beträgt 11 + 8 = 19.

Offenbar ist der Fluss jedes Schnitts durch das Netzwerk gerade gleich dem Wert des Flusses durch das Netzwerk, denn der Gesamtfluss durch das Netzwerk muss ja den Schnitt passieren. Im Beispiel hat jeder Schnitt einen Fluss von 19. Und offenbar kann somit der Gesamtfluss nicht größer sein als die Kapazität eines minimalen Schnitts. Durch das Netzwerk kann nicht mehr hindurchfließen als durch die engste Stelle hindurchpasst.Tatsächlich zeigt sich, dass sich der Gesamtfluss steigern lässt, bis er die Kapazität eines minimalen Schnitts erreicht, d.h. der maximale Fluss entspricht genau der Kapazität eines minimalen Schnitts [FF 56].

Der Schnitt in Bild 8 hat eine Kapazität von 23. Dieser Schnitt ist minimal. Entsprechend gibt es einen Fluss mit dem Wert 23, jedoch keinen mit größerem Wert. Tatsächlich haben wir im einleitenden Absatz bereits auf intuitive Weise einen Fluss mit dem Wert 23 gefunden.

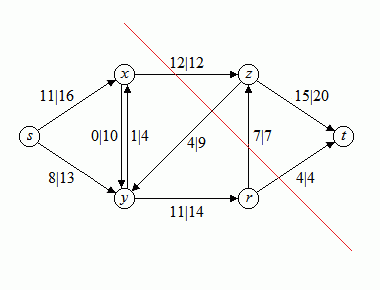
Bild 8: Schnitt mit minimaler Kapazität

Satz: (Ford, Fulkerson [FF 56])

Sei G = (V, E, c) ein Flussnetzwerk. Die folgenden drei Aussagen sind äquivalent:

Es gibt einen maximalen Fluss f mit Wert | f | in dem Flussnetzwerk;
im zu f zugehörigen Restkapazitäten-Netzwerk gibt es keinen Weg von der Quelle s zur Senke t;
ein minimaler Schnitt durch das Netzwerk hat die Kapazität | f |.

Die Klasse FlowNetwork modelliert ein Flussnetzwerk. Sie enthält die Methode computeMaxFlow zur Berechnung des Wertes eines maximalen Flusses. Zugleich wird ein minimaler Schnitt berechnet und in der ArrayList mincut gepeichert.

// modelliert ein Flussnetzwerk
public class FlowNetwork extends WeightedGraph
{

    public int s, t; // source, target
    public double[][] f; // flow
    public ArrayList<Integer> mincut;   // minimaler Schnitt

    // Konstruktor; Fluss wird mit 0 initialisiert
    public FlowNetwork(int n_)
    {
        super(n_, 0);  // noedge=0
        f=new double[n][n];
        for (int i=0; i<n; i++)
            for (int j=0; j<n; j++)
                f[i][j]=0;
     }

    // berechnet den Wert des Flusses, der aus der Quelle entspringt
    public double getFlowValue()
    {
        double flow=0;
        for (int j=0; j<n; j++)
            flow+=f[s][j];
        return flow;
    }

    // berechnet das Minimum der Kantengewichte entlang des
    // Wegs über die Knoten der Liste augmentationpath
    private double getMinCapacity(ArrayList<Integer> augmentationpath)
    {
        int i, j;
        MiniMaximizer<Double> min=new MiniMaximizer<Double>();
        Iterator<Integer> it=augmentationpath.iterator();
        i=it.next();
        while (it.hasNext())
        {
            j=it.next();
            min.add(getWeight(i, j));
            i=j;
        }
        return min.getMinVal();
    }

    // steigert den Fluss entlang des Wegs augmentationpath um flow;
    // reduziert die Restkapazitäten entsprechend
    private void augmentFlow(ArrayList<Integer> augmentationpath, double flow)
    {
        int i, j;
        Iterator<Integer> it=augmentationpath.iterator();
        i=it.next();
        while (it.hasNext())
        {
            j=it.next();
            f[i][j]+=flow;    // Wert des Flusses steigern
            setWeight(j, i, f[i][j]);  // Rückwärtskante
            addWeight(i, j, -flow);    // Vorwärtskante
            i=j;
        }
    }

    // berechnet den maximalen Fluss in einem Netzwerk;
    // sucht einen Steigerungsweg (augmentation path) im
    // Restkapazitäten-Netzwerk (residual network),
    // steigert den Fluss entsprechend und aktualisiert das
    // Restkapazitäten-Netzwerk, sucht erneut nach einem
    // Steigerungsweg, solange bis kein Steigerungsweg
    // mehr gefunden wird;
    // zum Schluss wird ein minimaler Schnitt (S, T) berechnet,
    // dargestellt durch die Menge S aller Knoten, die von der
    // Quelle s aus erreichbar sind
    public double computeMaxFlow()
    {
        ArrayList<Integer> augmentiationpath;  // Steigerungsweg
        BreadthFirstTree bft;   // Breitensuchbaum
        mincut=new ArrayList<Integer>();    // minimaler Schnitt
        double flow;

        while (true)
        {
            bft=new BreadthFirstTree(this, s);
            if (!bft.isReachable(t))
                break;
            augmentiationpath=bft.getPathTo(t);
            flow=getMinCapacity(augmentiationpath);
            augmentFlow(augmentiationpath, flow);
        }

        // minimalen Schnitt berechnen ( = alle Knoten, die
        // zum Schluss noch von der Quelle s aus erreichbar sind)
        for (int i=0; i<n; i++)
            if (bft.isReachable(i))
                mincut.add(i);

        return getFlowValue();
    }

}  // end class FlowNetwork

In der Funktion augmentFlow wird eine Vorwärtskante, sobald ihre Restkapazität den Wert 0 erreicht hat, automatisch gelöscht. Dies wird dadurch erreicht, dass im Konstruktor der Wert noedge mit 0 festgelegt wird. Kanten mit einer Kapazität 0 sind also nicht vorhandene Kanten.

Im Programm werden die Klassen WeightedGraph, BreadthFirstTree und MiniMaximizer verwendet.

Für den Test wird das Flussnetzwerk aus dem oben angegebenen Beispiel verwendet.

public class TestFlowNetwork
{
    public static void main(String[] args)
    {
        FlowNetwork w=new FlowNetwork(6);
        w.s=0;
        w.t=5;
        w.setWeight(0, 1, 16);
        w.setWeight(0, 2, 13);
        w.setWeight(1, 3, 12);
        w.setWeight(2, 4, 14);
        w.setWeight(1, 2, 10);
        w.setWeight(2, 1, 4);
        w.setWeight(3, 2, 9);
        w.setWeight(3, 5, 20);
        w.setWeight(4, 3, 7);
        w.setWeight(4, 5, 4);

        System.out.println(w);
        System.out.println("Maximaler Fluss: "+w.computeMaxFlow());
        System.out.println("Minimaler Schnitt: "+w.mincut);
    }

}

Weiter mit: [up]

H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 14.02.2017 Updated: 20.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden

Graphenalgorithmen

Maximaler Fluss

Problem

Modellierung

Fluss

Steigerungsweg

Finden von Steigerungswegen

Schnitt

Programm