Codierungstheorie
CRC-Verfahren
Bei der Speicherung und Übertragung von binär dargestellten Daten können durch Störungen einzelne Bits verfälscht werden. Um derartige Fehler zu erkennen, werden an die Daten Prüfbits angehängt.
Das einfachste Mittel zur Erkennung von Fehlern bei der Übertragung von Wörtern aus 𝔹+ ist das Anhängen eines Paritätsbits. Dies entspricht einer Codierung c : 𝔹+ → 𝔹+ mit
| c(x) = |  |
|
für alle x ∈ 𝔹+.
Nach dem Anhängen des zusätzlichen Bits haben alle Codewörter gerade Parität, d.h. eine gerade Anzahl von Einsen. Wird ein Wort mit ungerader Parität empfangen, so muss bei der Übertragung ein Fehler aufgetreten sein (z.B. eine Verfälschung eines einzelnen Bits). Dieser Fehler wird auf diese Weise erkannt.
Wird dagegen ein Wort mit gerader Parität empfangen, so sind zwei Fälle möglich: entweder es handelt sich um ein fehlerfrei übertragenes Codewort, oder es ist ein Fehler aufgetreten, der aber die Parität nicht verändert hat (z.B. durch Verfälschung von zwei Bits). Ein solcher Fehler wird nicht erkannt.
Unter der Annahme, dass Fehler mit einer geraden bzw. ungeraden Anzahl von verfälschten Bits gleich wahrscheinlich sind, werden im Mittel durch diese Art der Codierung 50% aller Fehler erkannt (nämlich diejenigen, in denen eine ungerade Anzahl von Bits verfälscht ist, denn hierdurch wird die Parität verändert), und 50% aller Fehler werden nicht erkannt.
Durch Anhängen von mehr als nur einem Prüfbit lässt sich die Fehlererkennungsrate drastisch steigern. Das CRC-Verfahren stellt eine Methode dar, um diese Prüfbits zu erzeugen.1)
Algebraische Grundlagen
Auf der Menge 𝔹 werden Verknüpfungen ⊕ und · definiert; hierbei entspricht die Verknüpfung ⊕ der Addition modulo 2 bzw. dem logischen Exklusiv-Oder, die Verknüpfung · entspricht der Multiplikation bzw. dem logischen Und.
Definition: Verknüpfungen ⊕ und · in 𝔹
|
|
Die Menge 𝔹 bildet mit diesen Operationen einen Körper, d.h. eine mathematische Struktur, in der man nach den gewohnten Rechenregeln addieren, subtrahieren, multiplizieren und dividieren kann.
Im Folgenden betrachten wir Polynome über dem Körper (𝔹, ⊕, ·).
Die Menge 𝔹[x] aller Polynome über 𝔹 ist ein Ring, d.h. eine Struktur, in der man addieren, subtrahieren und multiplizieren kann (z.B. ist die Menge ℤ der ganzen Zahlen auch ein Ring). Die Rechenoperationen in 𝔹[x] gehen aus den Rechenregeln des Körpers 𝔹 hervor.
Beispiel: (Polynom-Addition in 𝔹[x])
| f | = | x2 ⊕ x | = | 0·x3 ⊕ 1·x2 ⊕ 1·x1 ⊕ 0·x0 |
| g | = | x3 ⊕ x | = | 1·x3 ⊕ 0·x2 ⊕ 1·x1 ⊕ 0·x0 |
| f ⊕ g | = | x3 ⊕ x2 | = | 1·x3 ⊕ 1·x2 ⊕ 0·x1 ⊕ 0·x0 |
Beispiel: (Polynom-Multiplikation in 𝔹[x])
| f | = | x3 ⊕ x | ||
| g | = | x2 ⊕ x | ||
| f · g | = | x5 ⊕ x3 ⊕ x3 ⊕ x | = | x5 ⊕ x |
Anders als in einem Körper kann man aber in einem Ring nicht dividieren, sondern es gibt (wie in ℤ) nur eine Division mit Rest.
Satz: Seien f und g Polynome, g ≠ 0. Dann gibt es eine eindeutige Darstellung
f = q · g + r mit grad(r) < grad(g),
d.h. das Polynom r ist der Rest bei Division von f durch g, das Polynom q ist der Quotient.
Beispiel: (Division mit Rest in 𝔹[x])
| f | = | x5 | ||
| g | = | x2 + x | ||
| f | = | q · g ⊕ r | = | (x3 + x) · (x2 + x) ⊕ x |
Polynome aus 𝔹[x] lassen sich in einfacher Weise durch die Folge ihrer Koeffizienten darstellen.
Definition: Sei 𝔹n[x] ⊆ 𝔹[x] die Menge der Polynome p mit grad(p) < n. Dann entspricht jedem Polynom p ∈ 𝔹n[x] in natürlicher Weise ein Wort w ∈ 𝔹n, bestehend aus den Koeffizienten von p:
p = an-1xn-1 ⊕ . . . ⊕ a0x0
w = an-1 . . . a0
Wir identifizieren daher Polynome aus 𝔹n[x] und Wörter aus 𝔹n miteinander.
Beispiel: Sei p = x3 ⊕ x ∈ 𝔹6[x]. Dann ist
w = 0 0 1 0 1 0
das entsprechende Wort aus 𝔹6.
Definition: Sei g ein Polynom aus 𝔹n[x]. Der von g erzeugte Code C ⊆ 𝔹n ist die Menge aller Wörter, die Vielfachen von g in 𝔹n[x] entsprechen. Das Polynom g heißt Generatorpolynom von C.
Beispiel: Sei g = x ⊕ 1 und n = 4. Die folgende Tabelle zeigt alle Vielfachen von g in 𝔹4[x] sowie die entsprechenden Codewörter aus 𝔹4.
| (x ⊕ 1) · 0 | = | 0 | = | 0 0 0 0 |
| (x ⊕ 1) · 1 | = | x ⊕ 1 | = | 0 0 1 1 |
| (x ⊕ 1) · x | = | x2 ⊕ x | = | 0 1 1 0 |
| (x ⊕ 1) · (x ⊕ 1) | = | x2 ⊕ 1 | = | 0 1 0 1 |
| (x ⊕ 1) · x2 | = | x3 ⊕ x2 | = | 1 1 0 0 |
| (x ⊕ 1) · (x2 ⊕ 1) | = | x3 ⊕ x2 ⊕ x ⊕ 1 | = | 1 1 1 1 |
| (x ⊕ 1) · (x2 ⊕ x) | = | x3 ⊕ x | = | 1 0 1 0 |
| (x ⊕ 1) · (x2 ⊕ x ⊕ 1) | = | x3 ⊕ 1 | = | 1 0 0 1 |
Der erzeugte Code entspricht einem 3-Bit-Binärcode mit angehängtem Paritätsbit.
Der CRC-Algorithmus
Mithilfe des CRC-Algorithmus wird aus einer gegebenen Nachricht in systematischer Weise das zugehörige Codewort konstruiert. Zugrunde gelegt wird das Generatorpolynom; das erzeugte Codewort entspricht einem Vielfachen des Generatorpolynoms. Dies ist das Kriterium für die Fehlererkennung: alle Wörter, die nicht Vielfachen des Generatorpolynoms entsprechen, werden als fehlerhaft zurückgewiesen.
Algorithmus CRC
Eingabe:
Nachricht der Länge k (entsprechend einem Polynom p vom Grad < k), Generatorpolynom g vom Grad m
Ausgabe:
Codewort der Länge n = k + m (entsprechend einem Polynom h vom Grad < n)
Methode:
- multipliziere p mit xm (m Nullen an die Nachricht anhängen):
- f = p·xm
- teile das Ergebnis f durch das Generatorpolynom g und bilde den Rest r:
- f = q·g ⊕ r mit grad(r) < grad(g) = m
- addiere r zu f:
- h = f ⊕ r = q·g ⊕ r ⊕ r = q·g
Das Ergebnis h entspricht dem gesuchten Codewort; h ist durch g teilbar.
Durch die Addition von r in Schritt 3 findet nur innerhalb der letzten m Stellen eine Veränderung statt, da grad(r) < m ist. Das Codewort besteht also aus der ursprünglichen Nachricht mit angehängten m Prüfbits. Damit ist die Dekodierung eines Codewortes sehr einfach: Durch Weglassen der Prüfbits ergibt sich wieder die Nachricht.
Die Fehlererkennung wird durchgeführt, indem das dem empfangenen Wort entsprechende Polynom durch das Generatorpolynom geteilt wird. Ist der Rest ungleich Null, so ist ein Fehler aufgetreten.
Beispiel: Gegeben sei das Generatorpolynom g = x5 ⊕ x2 ⊕ x ⊕ 1, entsprechend dem Wort 1 0 0 1 1 1, sowie die Nachricht 1 0 0 1 0 1 1 1 0 0 1 1 1 0 1.
- multipliziere das Polynom p, das der Nachricht entspricht, mit x5 (5 Nullen an die Nachricht anhängen)
- teile das Ergebnis f durch das Generatorpolynom g und bilde den Rest r
1001011100111010000010011100001011001001110010111110011100100010100111000101100100111001011001001110010110
(das Wort 1 0 1 1 0 entspricht dem Rest r)
- addiere r zu f; das Ergebnis h entspricht dem gesuchten Codewort 1 0 0 1 0 1 1 1 0 0 1 1 1 0 1 1 0 1 1 0
Implementierung in Hardware
Die Polynomdivision lässt sich, nach dem im obigen Beispiel verwendeten normalen Divisionsverfahren, überraschend einfach in Hardware realisieren.
In Bild 1 dargestellt ist ein Schieberegister, in das von rechts das zu dividierende Polynom h hinein geschoben wird. Wenn eine 1 in der vordersten Schieberegisterzelle erscheint, wird das Generatorpolynom (in Bild 1 das Polynom 1 0 0 1 1 1) mit dieser 1 multipliziert (Und-Gatter) und an der entsprechenden Position von dem zu dividierenden Polynom h subtrahiert (Xor-Gatter).2) Der verbleibende Rest zusammen mit der nächstfolgenden Stelle von h wird anschließend um eine Position nach links geschoben. Wenn in der vordersten Schieberegisterzelle eine 0 erscheint, wird das 0-fache des Generatorpolynoms subtrahiert, d.h. es geschieht nichts, außer dass der Schieberegisterinhalt geschoben wird.
Es ist leicht zu sehen, dass durch diese Hardware genau das o.a. Divisionsverfahren realisiert wird. Wenn das zu dividierende Polynom h zu Ende ist, d.h. keine Stellen mehr in das Schieberegister eingegeben werden, steht im Schieberegister der Divisionsrest.
Die Schaltung kann sowohl zur Codierung als auch zur Fehlererkennung verwendet werden. Zur Fehlererkennung wird durch eine Oder-Schaltung überprüft, ob der Divisionsrest gleich Null oder ungleich Null ist. Zur Codierung wird der Divisionsrest an die Nachricht angehängt. Vor Beginn einer Division muss das Schieberegister gelöscht werden.
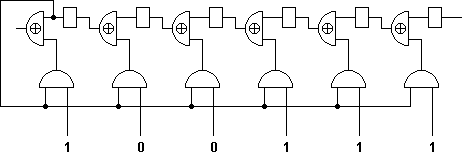
Bild 1: Schaltung zur Polynomdivision

Bild 2: Vereinfachte Schaltung (Linear Feed-Back Shift Register – LFSR)
Die Schaltung von Bild 1 kann vereinfacht werden, wenn das Generatorpolynom festliegt. Dann können alle Und-Gatter mit einer 1 am Eingang durch eine einfache Drahtverbindung ersetzt werden. Alle Und-Gatter mit einer 0 am Eingang liefern am Ausgang konstant 0 und können daher wegfallen; die entsprechenden Xor-Gatter mit dieser 0 am Eingang können durch Drahtverbindungen ersetzt werden. Das vorderste Xor-Gatter kann ebenfalls entfallen, da sein Ausgang nicht verwendet wird (er ist im Übrigen immer 0).
Bild 2 zeigt die vereinfachte Schaltung, ein rückgekoppeltes Schieberegister (Linear Feed-Back Shift Register – LFSR), für das Generatorpolynom 1 0 0 1 1 1.
Erkennung von Fehlern
Bei Auftreten eines Fehlers werden in dem gesendeten Wort ein oder mehrere Bits invertiert. Wird das Wort als Polynom aufgefasst, entspricht das Invertieren eines Bits der Addition eines Fehlerpolynoms, das eine 1 an dieser Position hat.
Beispiel: Durch Addition des Fehlerpolynoms 1 0 1 0 0 werden zwei Bits verfälscht.
Das gesendete Polynom h ist durch das Generatorpolynom g teilbar. Somit ist das empfangene Polynom h' = h⊕e genau dann durch das Generatorpolynom teilbar, wenn das Fehlerpolynom e durch das Generatorpolynom teilbar ist.
Wenn also das Fehlerpolynom ungleich Null ist und durch das Generatorpolynom teilbar ist, wird der Fehler nicht erkannt. Umgekehrt wird der Fehler erkannt, wenn das Fehlerpolynom nicht durch das Generatorpolynom teilbar ist.
Satz: Ist x⊕1 Teiler des Generatorpolynoms g, so wird jede ungerade Anzahl von Fehlern erkannt.
Beweis: Eine ungerade Anzahl von Fehlern entspricht einem Fehlerpolynom e mit einer ungeraden Anzahl von Einsen. Polynome mit einer ungeraden Anzahl von Einsen sind nicht durch x⊕1 teilbar. Dies kann man sich leicht anhand des Divisionsverfahrens klarmachen. Damit ist e nicht durch x⊕1 teilbar, also erst recht nicht durch g, d.h. der Fehler wird erkannt.
Eine wichtige Eigenschaft des CRC-Verfahrens ist die Fähigkeit, Mehrfachfehler zu erkennen, bei denen die verfälschten Bits innerhalb eines begrenzten Bereiches auftreten.
Definition: Ein Fehlerbündel der Länge b ist ein Fehler, bei dem die Position des ersten und des letzten falschen Bits den Abstand b-1 haben. Das einem Fehlerbündel der Länge b entsprechende Fehlerpolynom lässt sich schreiben als
e = e1 · xi mit grad(e1) = b-1.
Beispiel:
| Nachricht: | h = | 1 1 0 1 0 0 1 0 1 0 1 0 |
| Fehlerbündel der Länge 5: | e = | 1 0 0 1 1 0 0 0 |
| verfälschte Nachricht: | h ⊕ e = | 1 1 0 1 1 0 1 1 0 0 1 0 |
Es ist e = x7 ⊕ x4 ⊕ x3 = (x4 ⊕ x ⊕ 1) · x3 = e1 · x3.
Satz: Ist x kein Teiler des Generatorpolynoms g, so wird jedes Fehlerbündel der Länge b ≤ grad(g) erkannt.
Beweis: Es liege ein Fehlerbündel der Länge b ≤ grad(g) vor. Das entsprechende Fehlerpolynom sei
e = e1 · xi mit grad(e1) = b-1.
Angenommen, der Fehler wird nicht erkannt. Dann teilt das Generatorpolynom g das Fehlerpolynom e, d.h. es gilt
| g | e | ||
| ⇒ | g | xi · e1 | |
| ⇒ | g | e1, da x nicht Teiler von g | |
| ⇒ | grad(g) ≤ grad(e1) = b-1, | |
| im Widerspruch dazu, dass b ≤ grad(g) ist. |
In der Praxis werden u.a. folgende Generatorpolynome verwendet:
| CRC-16 (Magnetband) | x16 ⊕ x15 ⊕ x2 ⊕ 1 |
| CRC-CCITT (Disketten) | x16 ⊕ x12 ⊕ x5 ⊕ 1 |
| CRC-Ethernet | x32 ⊕ x26 ⊕ x23 ⊕ x22 ⊕ x16 ⊕ x12 ⊕ x11 ⊕ x10 ⊕ x8 ⊕ x7 ⊕ x5 ⊕ x4 ⊕ x2 ⊕ x ⊕ 1 |
Literatur
[RF 89] T.R.N. Rao, E. Fujiwara: Error-Control Coding for Computer Systems. Prentice Hall (1989)
[Lan 12] H.W. Lang: Algorithmen in Java. 3. Auflage, Oldenbourg (2012)
Das CRC-Verfahren finden Sie auch in meinem Buch über Algorithmen.
Weitere Themen des Buches: Sortieren, Textsuche, Graphenalgorithmen, Arithmetik, Codierung, Kryptografie, parallele Sortieralgorithmen.
Themen des Buches: Sortieren, Textsuche, Graphenalgorithmen, Arithmetik, Codierung, Kryptografie, parallele Sortieralgorithmen.
1) CRC steht für cyclic redundancy check.
2) Anstelle der DIN-Schaltsymbole sind hier die alten Schaltsymbole verwendet, aus denen die Signalflussrichtung (Eingänge/Ausgänge) deutlicher hervorgeht.
Weiter mit: [Huffman-Code] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 10.03.1997 Updated: 08.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden
