Zahlentheoretische AlgorithmenHensel-LiftungMultiplikativ inverses Element modulo einer Zweierpotenz bestimmen | |
Ziel ist es, das multiplikativ inverse Element a-1 einer ganzen Zahl a modulo einer Zweierpotenz n = 2k zu berechnen. Beispielsweise gilt 5·13  1 (mod 32), d.h. a-1 = 13 ist das multiplikativ inverse Element zu a = 5 modulo der Zweierpotenz n = 25 = 32. Natürlich aber geht es nicht um kleine Zahlen wie 5 und 13, sondern um sehr große Zahlen, etwa der Länge von 1024 Bit.
1 (mod 32), d.h. a-1 = 13 ist das multiplikativ inverse Element zu a = 5 modulo der Zweierpotenz n = 25 = 32. Natürlich aber geht es nicht um kleine Zahlen wie 5 und 13, sondern um sehr große Zahlen, etwa der Länge von 1024 Bit.
Die Berechnung des multiplikativ inversen Elements modulo einer Zweierpotenz wird beispielsweise bei der Montgomery-Multiplikation benötigt.
Das Standardverfahren zur Berechnung des multiplikativ inversen Elementes modulo n ist der erweiterte euklidische Algorithmus, dieser hat eine Zeitkomplexität von Θ(log(n)). Dies ist zwar schnell, aber in dem speziellen Fall, dass der Modul n eine Zweierpotenz ist, geht es schneller, nämlich in Zeit O(log(log(n))). Der entsprechende Algorithmus beruht auf einer zahlentheoretischen Methode, die als Hensel-Liftung (engl.: Hensel lifting) bekannt ist (nach K. Hensel ).
).
Die Methode eignet sich grundsätzlich auch für die Berechnung des multiplikativ inversen Elementes modulo pk mit p > 2.
Vorbemerkungen
Wenn zwei ganze Zahlen a und b beispielsweise kongruent modulo 1000 sind, wie etwa a = 7365 und b = 365, dann sind sie auch kongruent modulo 100 und kongruent modulo 10. Dies gilt allgemein für beliebige Modul-Potenzen.
Hilfssatz: Seien a, b 
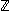 zwei ganze Zahlen und p, k
zwei ganze Zahlen und p, k 
 zwei natürliche Zahlen. Dann gilt für alle m
zwei natürliche Zahlen. Dann gilt für alle m 
 mit m
mit m k
k
a  b (mod pk)
b (mod pk) 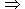 a
a  b (mod pm)
b (mod pm)
Die Kongruenz modulo einer Potenz von p überträgt sich also auf alle kleineren Potenzen von p.
Beweis:
Unter Anwendung der Definition von  gilt
gilt
a  b (mod pk)
b (mod pk) 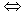 pk | a – b
pk | a – b 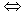 pk-m·pm | a – b
pk-m·pm | a – b 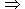 pm | a – b
pm | a – b 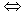 a
a  b (mod pm)
b (mod pm)
Beispiel: Für die Zahlen a = 20 und b = 4 sowie p = 2 und k = 3 gilt
20  4 (mod 8)
4 (mod 8)
und somit auch
20  4 (mod 4)
4 (mod 4)
20  4 (mod 2)
4 (mod 2)
Inverse Elemente
Wir benutzen den Hilfssatz zunächst für folgende Aussage über multiplikativ inverse Elemente.
Behauptung: Sei a-1 das inverse Element von a modulo pk. Dann gilt
a · a-1  1 (mod pk)
1 (mod pk)
Nach dem obigen Hilfssatz gilt dann aber auch für alle m 
 mit m
mit m k
k
a · a-1  1 (mod pm)
1 (mod pm)
d.h. a-1 ist auch invers zu a modulo pm.
Es ist also leicht, wenn das inverse Element von a modulo pk vorliegt, das inverse Element von a modulo einer kleineren Potenz pm zu berechnen. Gegebenenfalls ist eine Reduktion modulo pm erforderlich, damit das inverse Element in die Menge {0, ..., pm-1} fällt.
Beispiel: Es seien a = 3 sowie p = 10 und k = 5. Dann ist 66667 invers zu 3 modulo 100000.
3 · 66667  1 (mod 100000)
1 (mod 100000)
und somit auch invers zu 3 modulo aller kleineren Potenzen 10m, ggf. modulo 10m reduziert.
3 · 6667  1 (mod 10000)
1 (mod 10000)
3 · 667  1 (mod 1000)
1 (mod 1000)
3 · 67  1 (mod 100)
1 (mod 100)
3 · 7  1 (mod 10)
1 (mod 10)
An den obigen Zahlen wird deutlich, dass die Umkehrung nicht gilt. Modulo 10 gerechnet ist 7 zu 3 invers, modulo 100 gerechnet jedoch nicht. Es stellt sich die Frage, ob sich das inverse Element modulo 100 irgendwie in einfacher Weise aus dem inversen Element modulo 10 berechnen lässt. Die Antwort ist "ja", und zwar mit der Methode der Hensel-Liftung.
Lemma von Hensel
Das Lemma von Hensel macht eine sehr allgemeine Aussage über Nullstellen von Polynomen modulo Potenzen einer Primzahl. Mit dem speziellen Polynom f(x) = a·x – 1 liefert das Lemma von Hensel den Ansatz für die Berechnung von multiplikativ inversen Elementen modulo Potenzen einer Primzahl.
Lemma: (Hensel)
Sei f(x) ein Polynom mit ganzzahligen Koeffizienten. Ferner seien m, k 
 mit m
mit m k sowie r mit
k sowie r mit
f(r)  0 (mod pk)
0 (mod pk)
wobei aber
f '(r)  0 (mod p)
0 (mod p)
Hierbei bedeutet f '(x) die erste Ableitung von f(x).
Dann gibt es eine ganze Zahl s mit s  r (mod pk), derart dass
r (mod pk), derart dass
f(s)  0 (mod pk+m)
0 (mod pk+m)
Diese Zahl s lässt sich folgendermaßen berechnen (in 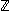 ); sie ist modulo pk+m eindeutig bestimmt:
); sie ist modulo pk+m eindeutig bestimmt:
s = r – f(r)·c
Hierbei ist c irgendeine ganze Zahl, für die gilt
c  (f '(r))-1 (mod pm)
(f '(r))-1 (mod pm)
Anwendung für multiplikativ inverse Elemente
Sei eine ganze Zahl a gegeben, a teilerfremd zu p. Um das multiplikativ inverse Element von a modulo pk zu berechnen, verwenden wir das Polynom
f(x) = a·x – 1
Seien zunächst m, k = 1. Wenn r = a-1 das multiplikativ inverse Element von a modulo p ist, gilt
f(r)  a·r – 1
a·r – 1  0 (mod p)
0 (mod p)
Die erste Ableitung von f(x) ist f '(x) = a. Damit gilt
f '(r) = a  0 (mod p)
0 (mod p)
denn a und p sind teilerfremd.
Die Voraussetzungen für das Lemma sind somit erfüllt. Gesucht ist nun eine Zahl s mit s  r (mod p), derart dass
r (mod p), derart dass
f(s)  0 (mod p2)
0 (mod p2)
Diese Zahl s lässt sich folgendermaßen berechnen (in 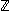 ), sie ist modulo p2 eindeutig bestimmt:
), sie ist modulo p2 eindeutig bestimmt:
s = r – f(r)·c
wobei für c gilt
c  (f '(r))-1
(f '(r))-1  a-1 (mod p)
a-1 (mod p)
Um also von r = a-1, dem inversen Element von a modulo p, zum inversen Element von a modulo p2 zu gelangen, berechnet man mit c = a-1 = r
s = r – f(r)·c = r – (a·r – 1) · r = (2 – a·r) · r
Damit das Ergebnis s in die Menge {0, ..., p2-1} fällt, wird es noch modulo p2 reduziert.
Beispiel
Bei dem verwendeten Polynom f(x) = a·x – 1 ist es noch nicht einmal erforderlich, dass p eine Primzahl ist. Im folgenden Beispiel verwenden wir p = 10.
Beispiel: Es seien a = 3 und p = 10. Das inverse Element von 3 modulo 10 ist r = 7. Um zum inversen Element von a modulo p2 zu gelangen, berechnen wir
s = (2 – a·r) · r = (2 – 3·7) · 7 = -19 · 7 = -133
Modulo 102 gerechnet gilt
-133  67 (mod 100)
67 (mod 100)
Damit ist 67 das inverse Element von 3 modulo 100.
Ausgehend vom inversen Element modulo p2 lässt sich in entsprechender Weise das inverse Element modulo p4 berechnen, usw. Das folgende Programm folgt diesem Ansatz.
Implementierung in Python
Es folgt ein entsprechendes Programm in der Programmiersprache Python.
Iterative Version
Das Programm berechnet das multiplikativ inverse Element von a modulo pk', wobei k' die kleinste Zweierpotenz ist, die größer oder gleich k ist. Wie oben gezeigt, ist das berechnete Ergebnis auch modulo aller kleineren Potenzen von p invers zu a.
# schnelle Berechnung des multiplikativ inversen Elements # von a modulo einer Potenz p^k # (iterative Version) def inv(a, p, k): e=1 r=modinverse(a, p) while e<k: e+=e p*=p r = (2-a*r) * r % p return r |
Der Aufruf inv(3, 10, 5) berechnet als das inverse Element von 3 modulo 105 den Wert 66666667. Dieser Wert ist invers zu 3 modulo 108, aber zugleich auch invers zu 3 modulo aller kleineren Potenzen von 10, also auch modulo 105. Eine Reduktion modulo pk wird am Schluss des Programms nicht durchgeführt, da der Wert pk hier nicht zur Verfügung steht.
Rekursive Version
In der rekursiven Version ist dies anders, der Wert n = pk steht hier zur Verfügung.
# schnelle Berechnung des multiplikativ inversen Elements # von a modulo einer Potenz p^k # (rekursive Version) def invr(a, p, k): if k==1: return modinverse(a, p) n=p**k a=a % n r=invr(a, p, (k+1)//2) return (2-a*r) * r % n |
Zu Anfang wird das multiplikativ inverse Element von a modulo p benötigt. Dieses wird mithilfe des erweiterten euklidischen Algorithmus durch die Funktion modinverse berechnet – ein wenig zusätzlicher Aufwand, aber für die relativ kleine Zahl p. Für p = 2 entfällt dieser Aufwand sogar völlig, denn das multiplikativ inverse Element zu einer (ungeraden) Zahl a ist stets 1.
Rekursive Version für Zweierpotenzen
Um beispielsweise das inverse Element von a modulo 25 zu berechnen, geht das rekursive Programm vom inversen Element von a modulo 23 aus und liftet es nach der oben angegebenen Formel. Das Ergebnis ist das inverse Element von a modulo 26, aber dieses wird unmittelbar modulo 25 reduziert.
Das inverse Element von a modulo 23 wird rekursiv aus dem inversen Element von a modulo 22 berechnet usw.
Das inverse Element einer ungeraden Zahl a modulo 21 ist stets 1; dies ist der Rückgabewert der Funktion für den Exponenten k = 1.
# schnelle Berechnung des multiplikativ inversen Elements # von a mit a ungerade modulo einer Zweierpotenz n = 2^k # (rekursive Version) def inv2(a, k): if k==1: return 1 n=2**k a=a % n r=inv2(a, (k+1)//2) return (2-a*r) * r % n |
Die Berechnung von n = 2k lässt sich effizient durch die Bit-Schiebeoperation 1<<k realisieren. Die Reduktion modulo n lässt sich effizient durch die Bit-Maskierungsoperation & n-1 realisieren.
Sinnvoll ist es dann, bereits nach der Berechnung von a·r eine Reduktion modulo n einzuschieben (und die Modulo-Operation natürlich durch eine Bit-Maskierungsoperation zu implementieren):
return (2-a*r%n) * r % n
|
Die folgende Funktion inv2s entspricht der vorigen Funktion inv2 mit dieser Änderung sowie mit der Anwendung von Bit-Schiebeoperationen und Bit-Maskierungsoperationen.
# schnelle Berechnung des multiplikativ inversen Elements # von a mit a ungerade modulo einer Zweierpotenz n = 2^k # (rekursive Version, mit Schiebe- und Maskierungsoperationen) def inv2s(a, k): if k==1: return 1 m=(1<<k)-1 a=a & m r=inv2s(a, (k+1)>>1) return (2-(a*r & m)) * r & m |
Zeitkomplexität
Wir gehen davon aus, dass p = 2 ist, dass also das multiplikativ inverse Element modulo einer Zweierpotenz gesucht ist. Dann verursacht der Aufruf der Funktion modinverse keinen Aufwand.
In der iterativen Version wird der Exponent e, beginnend bei 1, solange verdoppelt, bis er den Wert k erreicht oder überschritten hat. Dies ist nach 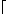 log(k)
log(k)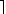 Schritten geschehen.
Schritten geschehen.
In der rekursiven Version wird der Wert von k solange halbiert, bis er den Wert 1 erreicht hat. Dies ist ebenfalls nach 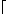 log(k)
log(k)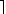 Schritten geschehen.
Schritten geschehen.
Die Zeitkomplexität der beiden Verfahren liegt demnach in O(log(k)) bzw. bezogen auf den Modul n = 2k in O(log(log(n))).
Implementierung in Haskell
Es folgen noch entsprechende Implementierungen der Funktionen inv sowie inv2 in der funktionalen Programmiersprache Haskell.
Für die Implementierung der iterativen Version wird eine Methode verwendet, die von einem Iterationsschema ausgeht, daraus Iterationsgleichungen ableitet und diese dann in systematischer Weise in ein Haskell-Programm überführt.
-- schnelle Berechnung des multiplikativ inversen Elements -- von a modulo einer Potenz p^k -- (iterative Version) inv :: Integer -> Integer -> Integer -> Integer inv a p k = iterate 1 p (modinverse a p) where iterate e p r | e>=k = r | otherwise = iterate (e+e) (p*p) ((2-a*r)*r `mod` (p*p)) |
Auch hier wird die Funktion modinverse verwendet, um zu Anfang das multiplikativ inverse Element von a modulo p zu berechnen.
Die rekursive Version zur Berechnung des multiplikativ inversen Elements modulo einer Zweierpotenz entspricht genau der entsprechenden Python-Funktion inv2.
-- schnelle Berechnung des multiplikativ inversen Elements -- von a mit a ungerade modulo einer Zweierpotenz n = 2^k inv2 :: Integer -> Integer -> Integer inv2 a 1 = 1 inv2 a k = (2-a*r) * r `mod` n where n = 2^k r = inv2 (a `mod` n) ((k+1) `div` 2) |
Literatur
| [BS 96] | E. Bach, J. Shallit: Algorithmic Number Theory. The MIT Press (1996) | |
| [Web 1] | https://arxiv.org/pdf/1209.6626 J.G. Dumas: On Newton-Raphson iteration for multiplicative inverses modulo prime powers (2018) | ||
| [Web 2] | https://link.springer.com/content/pdf/10.1007%2F978-3-319-96142-2_30.pdf C. Walther: Formally Verified Montgomery Multiplication (2018) | ||
| [Web 3] | https://doi.org/10.1145/3301317 C. Walther: Verified Newton–Raphson Iteration for Multiplicative Inverses Modulo Powers of Any Base. ACM Trans. Math. Softw. 45, 1, Article 9 (2019) | ||
| [Web 4] | https://en.wikipedia.org/wiki/Hensel%27s_lemma Wikipedia (englisch) | ||
Weiter mit:
 |
|
|
