Programmieren
Entwurf von endrekursiven Funktionen
In der funktionalen Programmierung werden Funktionen vielfach rekursiv definiert. Manchmal jedoch ist die rekursive Berechnung nicht effizient, wie etwa das Beispiel der Berechnung der Fibonacci-Zahlen zeigt. In derartigen Fällen lassen sich Funktionen auch auf bestimmte Weise endrekursiv (engl.: tail recursive) definieren; die Berechnung wird dann gleichsam iterativ durchgeführt.
In imperativen Programmiersprachen wird für den Entwurf von Iterationen in Form von While-Schleifen das Konzept eines (seqentiellen) Iterationsschemas verwendet. Die Aufstellung eines ähnlichen Iterationsschemas ist auch für den Entwurf von endrekursiven Funktionen geeignet, allerdings in Form eines parallelen Iterationsschemas. Im Folgenden wird dieses Konzept anhand von Beispielen in der funktionalen Programmiersprache Haskell vorgestellt.
Darüber hinaus gibt es die Möglichkeit, in bestimmten Fällen durch formale Manipulationen eine Umwandlung von Rekursion in Endrekursion vorzunehmen.
Iterationsschema
Ein Iterationsschema ist eine Tabelle, die für jede Iteration die Werte der beteiligten Variablen enthält. Für jede Variable, die während der Iteration ihren Wert ändert, ist eine Tabellenzeile vorgesehen.
Beispiel: Ein mögliches Iterationsschema für die Berechnung von an ist das folgende:
| i | 0 | 1 | 2 | 3 | 4 | ... | n |
| p | 1 | a | a·a | a·a·a | a·a·a·a | ... | an |
Die Variable i dient zum Zählen der Iterationen, die Variable p enthält das jeweilige Zwischenergebnis nach jeder Iteration. Für die Variable a ist keine Zeile im Iterationsschema vorgesehen, da sie ihren Wert im Verlauf der Berechnung nicht ändert. Das Ergebnis der Berechnung ist der Wert von p in der Spalte, in der i = n ist.
Iterationsgleichungen
Aus dem Iterationsschema werden Iterationsgleichungen abgeleitet. Für jede Variable des Iterationsschemas wird eine Iterationsgleichung aufgestellt. Diese gibt an, wie der Wert der Variablen in jeder Spalte des Schemas ab der zweiten Spalte zu berechnen ist. Die Werte in der ersten Spalte werden durch Initialisierung festgesetzt.
Beispiel: Die Iterationsgleichungen für das obige Iterationsschema lauten
- i = i' + 1
- p = p' · a
Hierbei bezeichnen Variablen "mit Strich" die Werte der entsprechenden Variablen in der vorherigen Spalte.
So ergibt sich der Wert von i in jeder Spalte als Wert von i in der vorherigen Spalte plus 1. Der Wert von p ergibt sich als Wert von p in der vorherigen Spalte mal a.
Die Iterationsgleichungen gelten in diesem Beispiel für alle Spalten des Iterationsschemas außer der ersten Spalte. Die Werte der ersten Spalte werden durch Initialisierung festgesetzt:
- i = 0
- p = 1
Sequentielles und paralleles Iterationsschema
Ein Iterationsschema, das sich für den Entwurf von While-Schleifen in der imperativen Programmierung eignet, wird als sequentielles Iterationsschema bezeichnet. In einem sequentiellen Iterationsschema werden die Werte aller Variablen in einer Spalte sequentiell, also einer nach dem anderen von oben nach unten berechnet. Die sequentielle Berechnung hat zur Folge, dass sobald eine Variable v in der aktuellen Spalte einen neuen Wert erhalten hat, der alte Wert dieser Variablen, also deren Wert v' aus der vorherigen Spalte, nicht mehr zur Verfügung steht.
Definition: Ein Iterationsschema wird als sequentielles Iterationsschema bezeichnet, wenn sich für jede darin auftretende Variable v eine Iterationsgleichung ableiten lässt, die auf der rechten Seite nur folgende Variablen enthält:
- Variablen w, die im Iterationsschema in derselben Spalte oberhalb von v stehen,
- Variablen w', die im Iterationsschema in der vorherigen Spalte auf gleicher Höhe oder unterhalb von v stehen,
- sonstige Variablen und Konstanten.
Im Gegensatz zum sequentiellen Iterationsschema steht das parallele Iterationsschema. In einem parallelen Iterationsschema werden die Werte der Variablen in einer Spalte parallel berechnet. Demzufolge stehen für die Berechnung dieser Werte ausschließlich die Werte der Variablen aus der vorherigen Spalte zur Verfügung (dafür aber alle).
Definition: Ein Iterationsschema wird als paralleles Iterationsschema bezeichnet, wenn sich daraus Iterationsgleichungen ableiten lassen, die für jede Variable v auf der rechten Seite nur folgende Variablen enthalten:
- Variablen w', die im Iterationsschema in der vorherigen Spalte stehen (ganz gleich in welcher Zeile),
- sonstige Variablen und Konstanten .
Anschaulich gesehen können für die Berechnung des Wertes einer Variablen an Position X im Iterationsschema alle Werte herangezogen werden, die im Iterationsschema an den Positionen x stehen (Bild 1: sequentielles Iterationsschema (a), paralleles Iterationsschema (b)).
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
| (a) | (b) |
Bild 1: Zugriff auf Werte an Position x: sequentielles Iterationsschema (a), paralleles Iterationsschema (b).
Ein Iterationsschema kann gleichzeitig ein sequentielles und ein paralleles Iterationsschema sein, nämlich dann, wenn für die Berechnung des Wertes einer Variablen an Position X nur Werte herangezogen werden, die in der vorherigen Spalte auf gleicher Höhe oder unterhalb von Position X stehen, also an Positionen x aus dem Durchschnitt der Positionen x von Bild 1 a und 1 b.
Für die Entwicklung von iterativen Haskell-Funktionen verwenden wir das parallele Iterationsschema. Den Wert einer Variablen v aus der vorherigen Spalte bezeichnen wir mit v'. In den Iterationsgleichungen, die wir in den folgenden Beispielen entwickeln, dürfen auf der rechten Seite also nur Variablen "mit Strich" vorkommen (jedenfalls wenn es sich um Variablen des Iterationsschemas und nicht um sonstige Variablen handelt).
Anwendung
Das Iterationsschema zur Berechnung von an aus dem obigen Beispiel ist ein paralleles Iterationsschema, denn in den Iterationsgleichungen kommen auf der rechten Seite nur Variablen "mit Strich" vor, es werden also nur Werte aus der vorherigen Spalte verwendet:
i = i' + 1
p = p' · a
mit den Anfangswerten
i = 0
p = 1
Das Iterationsschema lässt sich unmittelbar in folgendes Haskell-Programm überführen:
where
iterate i p | i==n = p
| otherwise = iterate (i+1) (p*a)
Die Funktion iterate bildet genau die Iterationsgleichungen nach. Der Aufruf von iterate zu Beginn enthält die Anfangswerte für i und p. Die Iteration endet, wenn der Spaltenindex i = n erreicht ist; dann wird als Ergebnis der Wert von p in dieser Spalte zurückgeliefert. Ansonsten ruft die Funktion iterate sich rekursiv selber auf, mit Parametern, die den rechten Seiten der Iterationsgleichungen entsprechen. Somit werden in den jeweiligen Aufrufen der Funktion iterate die Werte des Iterationsschemas von links nach rechts berechnet: iterate 0 1, iterate 1 a, iterate 2 a·a usw.
Weitere Beispiele
Das folgende Beispiel berechnet die Fakultätsfunktion.
Beispiel: (Fakultätsfunktion n!)
In folgendem Iterationsschema ergibt sich das Ergebnis n! als Wert der Variablen p in der Spalte, in der i = n gilt.
| i | 0 | 1 | 2 | 3 | ... |
| p | 1 | 1·1 | 1·1·2 | 1·1·2·3 | ... |
Die Iterationsgleichungen für i und p lauten:
- Iterationsgleichungen:
- i = i' + 1
- p = p'· (i'+1)
- Initialisierung:
- i = 0
- p = 1
- Abbruchbedingung:
- i = n
Das Iterationsschema erfüllt die Bedingungen eines parallelen Iterationsschemas. Auf der rechten Seite der Iterationsgleichungen kommen nur Variablen "mit Strich" vor, es werden also nur Werte aus der vorherigen Spalte verwendet. Das Iterationsschema lässt sich unmittelbar in folgendes Haskell-Programm überführen:
where
iterate i p | i==n = p
| otherwise = iterate (i+1) (p*(i+1))
Die Funktion iterate bildet genau die Iterationsgleichungen nach. Der Aufruf von iterate zu Beginn enthält die Anfangswerte für i und p. Die Iteration endet, wenn der Spaltenindex i = n erreicht ist; dann wird als Ergebnis der Wert von p in dieser Spalte zurückgeliefert. Ansonsten ruft sich die Funktion iterate rekursiv selber auf, mit Parametern, die den rechten Seiten der Iterationsgleichungen entsprechen. In den Aufrufen der Funktion iterate werden somit die Werte des Iterationsschemas von links nach rechts berechnet.
Beispiel: (n-te Fibonacci-Zahl)
Die Folge der Fibonacci-Zahlen f = 1, 1, 2, 3, 5, 8, 13, ... ist definiert durch die Rekursionsgleichungen
f0 = 1
f1 = 1
fn = fn-2 + fn-1
Es ist ein Leichtes, diese Rekursionsgleichungen in einer rekursiven Funktion zu implementieren. Es stellt sich jedoch heraus, dass für die Berechnung der n-ten Fibonacci-Zahl auf diese Weise mindestens fn Schritte erforderlich sind, also exponentiell viele. Bei iterativer Berechnung sind dagegen höchstens n Schritte erforderlich, also nur linear viele. Gesucht ist daher eine endrekursive Funktion, die diese iterative Berechnung nachbildet. Hierbei hilft wiederum die Aufstellung eines Iterationsschemas.
Ein Iterationsschema für die Berechnung der Fibonacci-Zahlen ist das folgende:
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | ... |
| f | 1 | 1 | 2 | 3 | 5 | 8 | 13 | ... |
| g | 0 | 1 | 1 | 2 | 3 | 5 | 8 | ... |
Die Iterationsgleichungen für i, f und g lauten:
- Iterationsgleichungen:
- i = i' + 1
- f = f ' + g'
- g = f '
- Initialisierung:
- i = 0
- f = 1
- g = 0
- Abbruchbedingung:
- i = n
Dies führt zu folgendem Haskell-Programm:
where
iterate i f g | i==n = f
| otherwise = iterate (i+1) (f+g) f
Die Funktion iterate bildet die Iterationsgleichungen nach. Der Aufruf von iterate zu Beginn enthält die Anfangswerte für i, f und g. Die Iteration endet, wenn der Spaltenindex i = n erreicht ist; dann wird als Ergebnis der Wert von f in dieser Spalte zurückgeliefert. In den Aufrufen der Funktion iterate werden somit die Werte des Iterationsschemas von links nach rechts berechnet.
Beispiel: (Binomialkoeffizienten)
Der Binomialkoeffizient 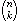 ist definiert als
ist definiert als
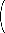
| n |
| k |
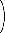 =
= | n! |
| k! · (n-k)! |
Da der Bruch durch (n-k)! gekürzt werden kann, gilt
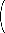
| n |
| k |
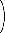 =
= | n · ... · (n-k+1) |
| 1 · ... · k |
Als Beispiel ist etwa
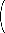
| 49 |
| 6 |
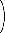 =
= | 49 · 48 · 47 · 46 · 45 · 44 |
| 1· 2 · 3 · 4 · 5 · 6 |
Ein Iterationsschema für dieses Beispiel ist das folgende:
| i | 49 | 48 | 47 | 46 | 45 | 44 | |
| j | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| p | 1 | · 49/1 | · 48/2 | · 47/3 | · 46/4 | · 45/5 | · 44/6 |
Die Schreibweise beispielsweise · 49/1 bedeutet, dass der Wert in der vorherigen Spalte dieser Zeile mit 49 multipliziert und dann durch 1 geteilt wird. Das Ergebnis 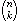 ergibt sich als der Wert von p in der Spalte, in der j = k+1 gilt.
ergibt sich als der Wert von p in der Spalte, in der j = k+1 gilt.
Aus dem Iterationsschema lassen sich folgende Iterationsgleichungen ableiten:
- Iterationsgleichungen:
- i = i' – 1
- j = j' + 1
- p = p' · i' div j'
- Initialisierung:
- i = n
- j = 1
- p = 1
- Abbruchbedingung:
- j = k + 1
Die Iterationsgleichungen lassen sich unmittelbar in ein entsprechendes iteratives Haskell-Programm umsetzen:
where
iterate i j p | j==k+1 = p
| otherwise = iterate (i-1) (j+1) (p*i `div` j)
Bemerkung: Das Progamm lässt sich noch optimieren, indem j==k+1 durch j==min k (n-k) + 1 ersetzt wird , denn es gilt, dass binom n k gleich binom n (n-k) ist.
Beispiel: (Sinusfunktion)
Ein etwas komplizierteres Beispiel ist die Berechnung der Sinusfunktion nach folgender Formel:
 n = 0, ...,
n = 0, ...,  (-1)n
(-1)n| x2n+1 |
| (2n+1)! |
Das entsprechende Iterationsschema enthält Variablen für den Index i = 2n+1, für den jeweiligen Summanden s und das zugehörige Vorzeichen v sowie für die jeweilige Partialsumme p.
| i | 1 | 3 | 5 | 7 | ... |
| v | 1 | -1 | 1 | -1 | ... |
| s | x1/1! | x3/3! | x5/5! | x7/7! | ... |
| p | 0 | + s' | - s' | + s' | ... |
Die Schreibweise + s' bedeutet, dass s' zum Wert in der vorherigen Spalte dieser Zeile addiert wird.
Die Iterationsgleichungen lauten:
- Iterationsgleichungen:
- i = i' + 2
- v = -v'
- s = s' · x2 / (i'+1) / (i'+2)
- p = p' + v' · s'
- Initialisierung:
- i = 1
- v = 1
- s = x
- p = 0
- Abbruchbedingung:
- s < 10-14
Dies führt zu folgendem Haskell-Programm (die Funktion ist zur Unterscheidung von der Standardfunktion sin mit sin' bezeichnet).
where
iterate i v s p | s<1e-14 = p
| otherwise = iterate (i+2) (-v) (s*x^2/(i+1)/(i+2)) (p+v*s)
Die Berechnung wird abgebrochen, sobald der neu hinzukommende Summand s kleiner als 10-14 geworden ist.
Zusammenfassung
Die Abfolge der Schritte bei einer Iteration lässt sich mithilfe eines Iterationsschemas anschaulich darstellen. Aus diesem Iterationsschema lassen sich Iterationsgleichungen ableiten. Und diese Iterationsgleichungen schließlich lassen sich durch rein formale Manipulation in ein entsprechendes Programm überführen.
Der schwierigste dieser drei Schritte ist der erste, die Aufstellung des Iterationsschemas. Welche Variablen werden für Zwischenergebnisse gebraucht? In welcher Reihenfolge sind sie zu berechnen? Diese Überlegungen sind im Zusammenhang damit anzustellen, dass sich aus dem Iterationsschema geeignete Iterationsgleichungen ableiten lassen. Der letzte Schritt, die Überführung der Iterationsgleichungen in ein Programm, ist der einfachste, denn er ist gleichsam rein mechanisch durchzuführen.
Aufgaben
Aufgabe 1: (Berechnung von π/4)
Die Leibniz-Reihe konvergiert (allerdings sehr langsam) gegen den Grenzwert π/4:
π/4 = 1 – 1/3 + 1/5 – 1/7 + 1/9 – 1/11 + 1/13 – ...
Stellen Sie ein paralleles Iterationsschema für die Berechnung von π/4 auf. Leiten Sie daraus die zugehörigen Iterationsgleichungen und Initialisierungen ab und setzen Sie diese in ein iteratives Haskell-Programm um. Brechen Sie die Berechnung ab, wenn der neu hinzukommende Summand betragsmäßig kleiner als 10-4 ist.
Aufgabe 2: (Berechnung von ln(2))
Eine schnell konvergierende Reihe zur Berechnung des natürlichen Logarithmus von 2 ist folgende:
| 2 |
| 1 · 31 |
| 2 |
| 3 · 33 |
| 2 |
| 5 · 35 |
Entwerfen Sie ein paralleles Iterationsschema für die Berechnung. Leiten Sie daraus die Iterationsgleichungen und Initialisierungen ab. Programmieren Sie eine entsprechende iterative Haskell-Funktion zur Berechnung von ln(2).
H.W. Lang mail@hwlang.de Impressum Datenschutz
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden