Theoretische Informatik
Reduktion von Wörtern
mit den Produktionen einer Grammatik
Mithilfe einer Grammatik lassen sich die Wörter einer Sprache L erzeugen: Ein Wort gehört zu L, wenn es sich durch eine Folge von bestimmten zulässigen Ersetzungen aus dem Startsymbol der Grammatik erzeugen lässt.
Aber auch der umgekehrte Weg ist möglich: Ein Wort gehört zu L, wenn es sich durch eine Folge von Ersetzungen – rückwärts angewandt – auf das Startsymbol zurückführen lässt.
Es ist wie beim Schreiben und beim Lesen: Beim Schreiben erzeugen wir grammatikalisch richtige Sätze; beim Lesen analysieren wir die grammatikalische Struktur von Sätzen.
Der Sinn eines Satzes erschließt sich erst aufgrund seiner grammatikalischen Struktur. Was ist Subjekt, Prädikat und Objekt?
Im Bereich der Programmierung verhält es sich ähnlich. Nur wenn ein Programm syntaktisch korrekt ist, lässt es sich in Maschinencode übersetzen und ausführen. Zunächst muss also geprüft werden, ob das Programm den Regeln der Grammatik der Programmiersprache entspricht. Sind alle Klammern richtig gesetzt? Fehlt irgendwo ein Semikolon?
Das Problem besteht also darin, zu entscheiden, ob ein bestimmtes Wort von einer gegebenen Grammatik erzeugt wird. Dieses Problem wird als Wortproblem bezeichnet.
Reduktion von Wörtern
Das Wortproblem lässt sich lösen, indem versucht wrd, das Wort w durch Anwendung der Produktionen der Grammatik – aber in umgekehrter Richtung – auf das Startsymbol der Grammatik zu reduzieren.
Eine solche umgekehrte Anwendung einer Produktion geschieht, indem in einem Wort w nach einem Vorkommen der rechten Seite einer Produktion gesucht wird und dieses Vorkommen durch die linke Seite der Produktion ersetzt wird. Das Ergebnis ist ein Wort w'.
Beispiel: Seien (S, aSb) und (S, ab) Produktionen und sei w = aabb. Zunächst wird die zweite Produktion in umgekehrter Richtung auf w angewendet, d.h. ab wird durch S ersetzt; das Ergebnis ist w' = aSb. Dann wird auf w' = aSb die erste Produktion wiederum in umgekehrter Richtung angewendet; es ergibt sich w'' = S.
Die umgekehrte Anwendung einer Produktion auf ein Wort w wird als Reduktionsschritt bezeichnet. Wie im Beispiel angedeutet, können mehrere Reduktionsschritte aufeinander folgen. Eine solche Folge von Reduktionsschritten wird als Reduktionsfolge bezeichnet.
Achtung: Die Produktionen dürfen stets nur einheitlich in einer Richtung angewendet werden, d.h. wir müssen uns entscheiden, ob wir ableiten oder reduzieren wollen.
Erkennung einer Sprache
Definition: Die von einer Grammatik G erkannte Sprache L(G) ist die Menge aller nur aus Terminalzeichen bestehenden Wörter, die sich auf das Startsymbol S reduzieren lassen:
L(G) = { w ∈ T* | w 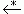 S }
S }
Beispiel: Gegeben sei folgende Grammatik G = (V, T, P, S) mit
V = {S}, T = {a, b}, P = { S → aSb, S → ab }
Das Wort aaabbb lässt sich in folgender Weise auf das Startsymbol S reduzieren: Zuerst wird durch umgekehrte Anwendung der zweiten Produktion in der Mitte ab durch S ersetzt. Das Ergebnis aaSbb wird durch umgekehrte Anwendung der ersten Produktion auf aSb reduziert, und schließlich wird aSb durch erneute umgekehrte Anwendung der ersten Produktion auf S reduziert. Die Folge aaabbb ← aaSbb ← aSb ← S ist die Reduktionsfolge für aaabbb.
Die von G erkannte Sprache ist
L(G) = { anbn | n ∈ ℕ } = { ab, aabb, aaabbb, ... }
Maschinelle Reduktion
Die Reduktion eines Wortes auf das Startsymbol lässt sich mechanisch mithilfe einer Maschine durchführen. Die Maschine muss in der Lage sein, Zeichenketten zu manipulieren. Das Programm der Maschine richtet sich nach einer gegebenen Grammatik.
Die Maschine erhält ein Wort w als Eingabe. Sie sucht dann in diesem Wort w nach einem Vorkommen einer rechten Seite einer Produktion der Grammatik und ersetzt dieses Vorkommen durch die zugehörige linke Seite. Das Ergebnis ist ein Wort w'. Mit diesem Wort w' verfährt sie in derselben Weise weiter – solange, bis keine Ersetzung mehr möglich ist. Wenn dann das Ergebnis das Startsymbol der Grammatik ist, erkennt die Maschine das Eingabewort w, ansonsten verwirft sie es.
Es kann im Allgemeinen mehrere Möglichkeiten geben, in einem Wort w Ersetzungen vorzunehmen. Es kann mehrere Vorkommen von rechten Seiten von Produktionen geben, und es kann mehrere Produktionen mit der gleichen rechten Seite geben. Wendet die Maschine in einer solchen Situation den falschen Reduktionsschritt an, so kann sie in eine Sackgasse geraten. Sie kann dann irgendwann keine Ersetzungen mehr vornehmen, hat aber noch nicht das Startsymbol erreicht. Sie weist dann das Eingabewort w zurück, obwohl es in Wirklichkeit eine Reduktionsfolge gibt, die w auf das Startsymbol reduziert.
Um dieses Problem zu vermeiden, verwenden wir eine nichtdeterministische Maschine. Eine nichtdeterministische Maschine wählt, sozusagen mit schlafwandlerischer Sicherheit, immer den richtigen Reduktionsschritt.
Zusammenfassung
Mithilfe einer Grammatik und ihrer Produktionen lassen sich aus dem Startsymbol durch eine Folge von Ersetzungen Wörter erzeugen. Alle Wörter, die sich aus dem Startsymbol erzeugen lassen und die nur aus Terminalzeichen bestehen, bilden die von der Grammatik erzeugte Sprache.
Genau diese Wörter lassen sich durch umgekehrte Anwendung der Produktionen auf das Startsymbol reduzieren. Ableiten und Reduzieren ist also dasselbe, nur in umgekehrter Richtung.
Die Reduktion eines Wortes auf das Startsymbol der Grammatik erfolgt durch eine Folge von Ersetzungen, bei denen jeweils ein Vorkommen der rechten Seite einer Produktion durch die entsprechende linke Seite ersetzt wird.
Diese Ersetzungen lassen sich mithilfe einer Maschine durchführen; im Folgenden wird eine solche Maschine vorgestellt.
Weiter: [String-Turingmaschine] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 26.01.2003 Updated: 16.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden