Theoretische Informatik
Konstruktion einer rechtslinearen Grammatik
aus einem nichtdeterministischen endlichen Automaten
Gegeben ist ein nichtdeterministischer endlicher Automat N. Es stellt sich die Frage, ob es eine Grammatik G gibt mit L(G) = L(N). Gesucht ist also eine Grammatik, die genau die Sprache erzeugt, die der Automat N erkennt. Wir formen dazu den gegebenen nichtdeterministischen Automaten N in geeigneter Weise in eine Grammatik um. Dabei zeigt es sich, dass sogar ein ganz bestimmter Typ von Grammatik hierfür ausreichend ist. Ferner zeigt sich, dass "Erkennen" und "Erzeugen" im Prinzip das gleiche ist, nur in entgegengesetzter Richtung.
Verfahren
Gegeben sei ein nichtdeterministischer endlicher Automat
N = (Z, A, d, q, F)
mit Zustandsmenge Z, Eingabealphabet A, Übergangsrelation d, Startzustand q und Menge von Endzuständen F.
Aus dem Automaten N wird in folgender Weise eine Grammatik
G = (V, T, P, S)
mit Variablenmenge V, Terminalzeichenmenge T, Produktionenmenge P und Startsymbol S konstruiert.
Konstruktion der Grammatik
- Die Menge der Variablen V der Grammatik ist gleich der Menge der Zustände Z des Automaten:
V = Z
- Das Startsymbol S der Grammatik ist gleich dem Startzustand q des Automaten:
S = q
- Die Menge der Terminalzeichen T der Grammatik ist gleich dem Eingabealphabet A des Automaten:
T = A
- Die Menge der Produktionen P der Grammatik entsteht aus der Übergangsrelation d des Automaten wie folgt:
- Für alle a ∈ A und r, s ∈ Z gilt
(r, a, s) ∈ d ⇔ r → as ∈ P
- Für alle r ∈ Z gilt
r ∈ F ⇔ r → ε ∈ P
Aus jedem Element (r, a, s) der Übergangsrelation wird also eine Produktion r → as gemacht. Zusätzlich wird für jeden Endzustand r ∈ F noch eine Produktion r → ε erzeugt.
- Für alle a ∈ A und r, s ∈ Z gilt
Jedem Wort, das der Automat erkennt, entspricht ein Pfad durch den Zustandsgraphen des Automaten vom Startzustand zu einem Endzustand. Diesem Pfad entspricht eine Ableitungsfolge vom Startsymbol der Grammatik zu diesem Wort. Umgekehrt entspricht jeder Ableitungsfolge vom Startsymbol der Grammatik zu einem Terminalwort ein Pfad durch den Zustandsgraphen des Automaten vom Startzustand zu einem Endzustand.
Beispiel: Der in folgendem Bild 1 dargestellte nichtdeterministische endliche Automat N erkennt die Sprache
L = { alle Wörter über A = {a, b}, die mit a anfangen und mit a aufhören }
Die aus dem Automaten N konstruierte Grammatik G = (V, T, P, S) hat die Variablen V = {S, X, Y}, die Terminalzeichen T = {a, b}, die Produktionen
| S |  | aX | aY |
| X |  | aX | bX | aY |
| Y |  | ε |
und das Startsymbol S. Die Grammatik erzeugt die Sprache L.
Dem Wort abba entspricht der Pfad von S über X nach Y im Automaten. Diesem Pfad entspricht die Ableitungsfolge
S → aX → abX → abbX → abbaY → abba
in der Grammatik.
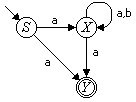
Bild 1: Nichtdeterministischer endlicher Automat, der die Sprache L erkennt
Rechtslineare Grammatik
Die Grammatik, die durch die angegebene Konstruktion entsteht, ist eine rechtslineare Grammatik.
Definition: Eine Grammatik G = (V, T, P, S) heißt rechtslinear, wenn jede Produktion von der Form
| X |  | aY | oder |
| X |  | a | oder |
| X |  | ε |
mit X, Y ∈ V und a ∈ T ist.
Eine rechtslineare Grammatik ist nichts anderes als eine Typ-3-Grammatik der Chomsky-Hierarchie.
Satz: Jede reguläre Sprache ist eine Typ-3-Sprache.
Beweis: Wenn eine Sprache L regulär ist, dann gibt es einen nichtdeterministischen endlichen Automaten N, der sie erkennt, d.h. L(N) = L. Aus diesem Automaten kann nach dem oben angegebenen Verfahren eine Typ-3-Grammatik G konstruiert werden mit L(G) = L(N) = L.
Aufgaben
Aufgabe 1: Gegeben sei folgender nichtdeterministische Automat N (Bild 2). Konstruieren Sie nach dem angegebenen Verfahren eine rechtslineare Grammatik G mit L(G) = L(N).
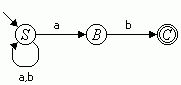
Bild 2: Nichtdeterministischer endlicher Automat N
Aufgabe 2: Beweisen Sie das Pumping Lemma mithilfe des Begriffs der rechtslinearen Grammatik.
Aufgabe 3: Geben Sie das umgekehrte Verfahren an, das zu einer rechtslinearen Grammatik G einen nichtdeterministischen endlichen Automaten N, ggf. mit Epsilon-Übergängen, konstruiert, derart dass L(G) = L(N) gilt.
Weiter mit: [Kontextfreie Grammatik] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 26.01.2003 Updated: 16.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden