Theoretische Informatik
Abgeschlossenheitseigenschaften regulärer Sprachen
Reguläre Sprachen entstehen durch eine endliche Folge von Anwendungen der Operationen Vereinigung und Verkettung sowie Abschluss auf Elementarsprachen. Daher ergeben die Vereinigung und die Verkettung von regulären Sprachen sowie der Abschluss einer regulären Sprache wiederum eine reguläre Sprache.
Vereinigung, Verkettung, Abschluss
Satz: Seien L0 und L1 reguläre Sprachen über einem Alphabet A. Dann sind die Vereinigung L = L0 ∪ L1, die Verkettung L = L0L1 und der Abschluss L = L0* wiederum reguläre Sprachen.
Beweis: Seien X0 und X1 die regulären Ausdrücke, die L0 bzw. L1 erzeugen. Dann erzeugt der reguläre Ausdruck X0 | X1 die Sprache L = L0 ∪ L1, der reguläre Ausdruck X0X1 die Sprache L = L0L1 und der reguläre Ausdruck X0* die Sprache L = L0*. Also ist die jeweilige erzeugte Sprache L regulär.
Komplement und Durchschnitt
Satz: Sei L eine reguläre Sprache über einem Alphabet A. Dann ist das Komplement L = A* \ L wiederum eine reguläre Sprache.
Beweis: Sei D ein deterministischer endlicher Automat, der L erkennt. Der Automat D erreicht für jedes Wort w ∈ L einen Endzustand und für jedes Wort w ∉ L einen Nicht-Endzustand. Indem in D alle Endzustände zu Nicht-Endzuständen gemacht werden und umgekehrt, entsteht ein deterministischer endlicher Automat D, der L erkennt. Also ist L regulär.
Beispiel: Der folgende deterministische endliche Automat (Bild 1a) erkennt die Sprache aller Wörter über {a, b}, die mit a anfangen und mit a aufhören. Der andere deterministische endliche Automat (Bild 1b) erkennt das Komplement dieser Sprache, also alle Wörter, die mit b anfangen oder mit b aufhören sowie das leere Wort.
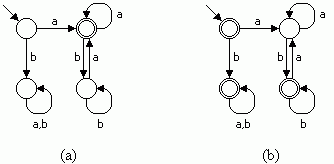
Bild 1: Deterministische endliche Automaten für eine reguläre Sprache und ihr Komplement
Satz: Seien L0 und L1 reguläre Sprachen über einem Alphabet A. Dann ist der Durchschnitt L = L0 ∩ L1 wiederum eine reguläre Sprache.
Spiegelbild
Definition: Das Spiegelbild eines Wortes x = x0 ... xn-1 ist das Wort
xR = xn-1 ... x0,
also das Wort x rückwärts gelesen. Das Spiegelbild einer Sprache L ist die Sprache
LR = { xR | x ∈ L },
also die Menge der gespiegelten Wörter von L.
Satz: Sei L eine reguläre Sprache. Dann ist das Spiegelbild LR wiederum eine reguläre Sprache.
Beweis: Siehe Aufgabe 2.
Aufgaben
Aufgabe 1: Im Beweis des Satzes, dass das Komplement einer regulären Sprache wieder regulär ist, wird ein deterministischer endlicher Automat verwendet. Geben Sie ein möglichst einfaches Beispiel dafür an, dass der Beweis im Allgemeinen nicht funktioniert, wenn der endliche Automat nicht deterministisch ist.
Aufgabe 2: Zeigen Sie: Das Spiegelbild einer regulären Sprache ist regulär.
Weiter mit: [Pumping-Lemma] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 21.01.2010 Updated: 16.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden
