Programmieren
Entwurf von Programmschleifen
Wie entwirft man eine Programmschleife? Im Folgenden wird eine systematische Methode hierzu angegeben. Diese beruht auf der Erstellung eines Iterationsschemas, aus dem Iterationsgleichungen abgeleitet werden. Diese wiederum lassen sich unmittelbar in eine Programmschleife umsetzen.
Die Programmschleifen sind hier in der Programmiersprache Java angegeben; eine entsprechende Python-Version stehen ebenfalls zur Verfügung.
In funktionalen Programmiersprachen wie etwa Haskell treten endrekursive Funktionen an die Stelle von Iteration. Auch hier lassen sich mithilfe eines parallelen Iterationsschemas in systematischer Weise Iterationsgleichungen gewinnen, die unmittelbar in entsprechende endrekursive Funktionsdefinitionen umgesetzt werden können.
Iterative Berechnungen
Ein wichtiges Anwendungsgebiet für Programmschleifen ist die iterative Berechnung von Funktionswerten.
Beispiel: Die Berechnung von an, von n!, von ex, von π, von Binomialkoeffizienten usw. lässt sich durch Iterationsverfahren durchführen.
So lässt sich etwa an berechnen, indem der Anfangswert 1 n-mal mit a multipliziert wird. Der Funktionswert von ex ergibt sich als Grenzwert einer Reihe. Ebenso lässt sich π durch eine Folge oder Reihe approximieren.
Iterationsschema
Ein Iterationsschema ist eine Tabelle, die für jede Iteration die Werte der beteiligten Variablen enthält. Für jede Variable, die während der Iteration ihren Wert ändert, ist eine Tabellenzeile vorgesehen.
Beispiel: Ein mögliches Iterationsschema für die Berechnung von an ist das folgende:
| i | 0 | 1 | 2 | 3 | 4 | ... | n |
|---|---|---|---|---|---|---|---|
| p | 1 | a | a·a | a·a·a | a·a·a·a | ... | an |
Die Variable i dient zum Zählen der Iterationen, die Variable p enthält das jeweilige Zwischenergebnis nach jeder Iteration. Für die Variable a ist keine Zeile im Iterationsschema vorgesehen, da sie ihren Wert im Verlauf der Berechnung nicht ändert. Das Ergebnis der Berechnung ist der Wert von p in der Spalte, in der i = n ist.
Iterationsgleichungen
Aus dem Iterationsschema werden Iterationsgleichungen abgeleitet. Für jede Variable des Iterationsschemas wird eine Iterationsgleichung aufgestellt. Diese gibt an, wie der Wert der Variablen in jeder Spalte des Schemas ab der zweiten Spalte zu berechnen ist. Die Werte in der ersten Spalte werden durch Initialisierung festgesetzt.
Beispiel: Die Iterationsgleichungen für das obige Iterationsschema lauten
- i = i' + 1
- p = p' · a
Hierbei bezeichnet v' den Wert der Variablen v in der vorherigen Spalte.
So ergibt sich der Wert von i in jeder Spalte als Wert von i in der vorherigen Spalte plus 1. Der Wert von p ergibt sich als Wert von p in der vorherigen Spalte mal a.
Die Iterationsgleichungen gelten in diesem Beispiel für alle Spalten des Iterationsschemas außer der ersten Spalte. Die Werte der ersten Spalte werden durch Initialisierung festgesetzt:
- i = 0
- p = 1
Regeln für die Aufstellung der Iterationsgleichungen
Die Iterationsgleichungen lassen sich unmittelbar in ein Programm umsetzen, wenn die folgenden Regeln eingehalten werden.
- Die Reihenfolge der Variablen im Iterationsschema bestimmt die Reihenfolge der Iterationsgleichungen
- Die Iterationsgleichung für eine Variable v darf auf der rechten Seite nur folgende Variablen enthalten:
- Variablen w, die im Iterationsschema in derselben Spalte oberhalb von v stehen,
- Variablen w', die im Iterationsschema in der vorherigen Spalte auf gleicher Höhe oder unterhalb von v stehen,
- sonstige Variablen und Konstanten.
- Alle Variablen v, die in der Form v' auftreten, müssen initialisiert werden.
Anschaulich gesehen dürfen für die Berechnung eines Wertes im Iterationsschema nur die darüberliegenden Werte oder die direkt links daneben und darunter liegenden Werte des Iterationsschemas benutzt werden. So dürfen für die Berechnung des Wertes an Position X nur Werte aus den mit x gekennzeichneten Feldern verwendet werden (und natürlich Werte von sonstigen Variablen und Konstanten).
| x | ||||
| x | ||||
| x | X | |||
| x | ||||
| x |
Bild 1: Zulässige Variablen auf der rechten Seite einer Iterationsgleichung
Beispiel: In den obigen Iterationsgleichungen
i = i' + 1
p = p' · a
kommt auf der rechten Seite der Gleichung für i nur die Variable i' vor, die im Iterationsschema nicht oberhalb von i steht, sowie die Konstante 1. Auf der rechten Seite der Gleichung für p kommt nur die Variable p' vor, die im Iterationsschema nicht oberhalb von p steht, sowie die sonstige Variable a.
Bemerkung: Ein Iterationsschema lässt sich auch für die funktionale Programmierung mit der Programmiersprache Haskell verwenden. In der funktionalen Programmierung muss das Iterationsschema ein paralleles Iterationsschema sein, im Gegensatz zum oben definierten sequentiellen Iterationsschema. Bei einem parallelen Iterationsschema werden für die Berechnung der Werte nur Werte aus der vorherigen Spalte verwendet – die rechten Seiten der Iterationsgleichungen enthalten also nur Variablen "mit Strich". Das obige Iterationsschema für die Berechnung von an ist ein paralleles Iterationsschema – und zugleich auch ein sequentielles Iterationsschema, diese Eigenschaften schließen sich also nicht aus.
Umsetzung der Iterationsgleichungen in ein While-Programm
Die nach den obigen Regeln aufgestellten Iterationsgleichungen lassen sich direkt in eine While-Schleife umsetzen. Vor die While-Schleife wird die Deklaration und Initialisierung der beteiligten Variablen gesetzt. Als Schleifenbedingung wird eine Bedingung gewählt, die im Iterationsschema für alle Spalten vor der Spalte gilt, in der das Ergebnis der Berechnung erwartet wird.
Beispiel: Das Beispiel zur Berechnung von an ergibt, unter Benutzung der entsprechenden Iterationsgleichungen und Initialisierungen, folgendes Programmstück. Vorausgesetzt ist, dass die Variablen a und n bereits deklariert sind und Werte enthalten. Das Ergebnis der Berechnung ist der Wert von p nach Beendigung der Schleife.
while (i<n)
{
i=i+1;
p=p*a;
}
Ermitteln einer Schleifeninvariante aus dem Iterationsschema
Für die formale Programmverifikation wird eine Schleifeninvariante benötigt; dies ist eine Bedingung, die beim Eintritt in den Schleifenkörper gilt und zum Schluss des Schleifenkörpers wiederum gilt.
Aus dem oben angegebenen Iterationsschema lässt sich eine solche Schleifeninvariante P ablesen – es ist eine Bedingung, die für alle Spalten vor und einschließlich der Spalte gilt, in der das Ergebnis erwartet wird. Die Bedingung lautet:
P : p = ai ∧ i ≤ n
Weitere Iterationsschema-Beispiele
Berechnung von ln(2) durch alternierende Reihe
Die alternierende harmonische Reihe konvergiert (allerdings sehr langsam) gegen den Grenzwert ln(2).
ln(2) = 1 – 1/2 + 1/3 – 1/4 + 1/5 – 1/6 + ...
Für die Berechnung der Reihe wird folgendes Iterationsschema verwendet:
| n | 0 | 1 | 2 | 3 | 4 | 5 | ... |
| s | 1/1 | 1/2 | 1/3 | 1/4 | 1/5 | ... | |
| v | -1 | 1 | -1 | 1 | -1 | 1 | ... |
| p | 0 | 1 | 1-1/2 | 1-1/2+1/3 | ... |
Die Variable n zählt die Iterationen, s enthält jeweils das nächste Reihenglied, v das zugehörige Vorzeichen und p die jeweils aufgelaufene Partialsumme.
Aus dem Iterationsschema lassen sich folgende Iterationsgleichungen gewinnen:
- n = n' + 1
- s = 1/n
- v = –v'
- p = p' + v · s
Auf den rechten Seiten der Iterationsgleichungen werden nur Variablen verwendet, die nach dem Schema von Bild 1 zulässig sind.
Die Iterationsgleichungen gelten ab der zweiten Spalte. Die Initialisierung für die erste Spalte ist
- n = 0
- v = -1
- p = 0
Die Iterationsgleichungen und Initialisierungen werden in folgendes While-Programm umgesetzt. Die Schleife wird 1000-mal durchlaufen. Das Ergebnis ist der Wert von p nach Ende der Iteration.
double s, p=0;
while (n<1000)
{
n=n+1;
s=1.0/n;
v=-v;
p=p+v*s;
}
Berechnung der Fibonacci-Zahlen
In der Fibonacci-Folge ergibt sich jedes Folgenelement als Summe der beiden vorhergehenden Elemente:
f = 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...
Für die Berechnung der Folge wird folgendes Iterationsschema verwendet:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ... |
| h | 1 | 1 | 2 | 3 | 5 | 8 | ... | |
| g | 1 | 1 | 2 | 3 | 5 | 8 | 13 | ... |
| f | 1 | 2 | 3 | 5 | 8 | 13 | 21 | ... |
Aus dem Iterationsschema lassen sich folgende Iterationsgleichungen gewinnen:
- i = i' + 1
- h = g'
- g = f '
- f = g + h
Die Iterationsgleichungen gelten ab der zweiten Spalte. Die Initialisierung für die erste Spalte ist
- i = 1
- g = 1
- f = 1
Die Iterationsgleichungen und Initialisierungen werden in folgendes While-Programm umgesetzt, das hier in eine Funktionsdefinition für die Berechnung der n-ten Fibonacci-Zahl eingesetzt ist (n = 0, 1, 2, 3, ...). Für die 0-te Fibonacci-Zahl ist keine gesonderte Behandlung erforderlich, da die Initialisierung f = 1 auch für n = 0 gültig ist.
{
int i=1;
long h, g=1, f=1;
while (i<n)
{
i=i+1;
h=g;
g=f;
f=g+h;
}
return f;
}
Aufgaben
Aufgabe 1: (Berechnung der eulerschen Zahl e)
Die folgende Reihe konvergiert gegen die eulersche Zahl e = 2,71828...:
n = 0, ..., 
| 1 |
| n! |
| 1 |
| 0! |
| 1 |
| 1! |
| 1 |
| 2! |
| 1 |
| 3! |
| 1 |
| 4! |
Stellen Sie ein Iterationsschema für die Berechnung von e auf. Leiten Sie daraus die zugehörigen Initialisierungen und Iterationsgleichungen ab und setzen Sie diese in eine While-Schleife um. Brechen Sie die While-Schleife ab, wenn der neu hinzugekommene Summand kleiner als 10-14 ist.
Erstellen Sie unter Benutzung dieser While-Schleife eine Funktion double e() zur Berechnung von e.
Aufgabe 2: (Berechnung von π)
Die Leibniz-Reihe konvergiert (allerdings sehr langsam) gegen den Grenzwert π/4:
π/4 = 1 – 1/3 + 1/5 – 1/7 + 1/9 – 1/11 + 1/13 – ...
Stellen Sie ein Iterationsschema für die Berechnung von π/4 auf. Leiten Sie daraus die zugehörigen Initialisierungen und Iterationsgleichungen ab und setzen Sie diese in eine While-Schleife um. Brechen Sie die While-Schleife ab, wenn der neu hinzugekommene Summand betragsmäßig kleiner als 10-4 ist.
Erstellen Sie unter Benutzung dieser While-Schleife eine Funktion double pi() zur (grob angenäherten) Berechnung von π.
Aufgabe 3: (Berechnung von Binomialkoeffizienten)
Der Binomialkoeffizient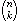 
ist definiert als
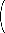
| n |
| k |
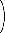= | n! |
| k! · (n-k)! |
Da der Bruch durch (n-k)! gekürzt werden kann, gilt
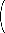
| n |
| k |
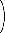= | (n-k+1) · ... · n |
| 1 · ... · k |
Als Beispiel ist etwa
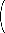
| 49 |
| 6 |
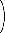= | 44 · 45 · 46 · 47 · 48 · 49 |
| 1· 2 · 3 · 4 · 5 · 6 |
Stellen Sie ein Iterationsschema für die Berechnung von 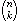auf. Leiten Sie daraus die zugehörigen Initialisierungen und Iterationsgleichungen ab und setzen Sie diese in eine While-Schleife um, innerhalb einer Funktion long binom(long n, long k).
Weitere Aufgaben ...
Weiter mit: [Datentyp String] [Literatur] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden