Programmverifikation
Korrektheit von While-Schleifen
Partielle Korrektheit
Die Schlussregel für die While-Schleife ergibt sich aus dem Flussdiagramm (Bild 1). Sie lautet
| P ∧ ¬B ⇒ R, {P ∧ B} S {P} |
| {P} while(B) S {R} |
Die Schlussregel besagt, dass wenn die Prämissen P ∧ ¬B ⇒ R und {P ∧ B} S {P} erfüllt sind, der Schluss {P} while(B) S {R} gültig ist. Hierbei gilt die Nachbedingung R allerdings nur, wie in Bild 1 zu sehen, wenn die Schleife verlassen wird, wenn die Schleife also terminiert. Korrektheit unter dieser Voraussetzung wird als partielle Korrektheit bezeichnet, im Gegensatz zur totalen Korrektheit.
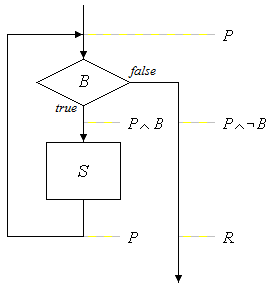
Bild 1: Vor- und Nachbedingungen bei der While-Schleife
Die Bedingung P in Bild 1 ist die Schleifeninvariante. Der Begriff Invariante bedeutet, dass die Bedingung vor Eintritt in den Schleifenkörper und danach unverändert gilt.
Beispiel: Das folgende Programmstück berechnet n! = 1 · 2 · 3 · ... · n.
f=1;
while (i<n)
{
i=i+1;
f=f*i;
}
Das Ergebnis n! soll am Ende des Programms als Wert der Variablen f erscheinen. Die Nachbedingung des Programms lautet also
R: f = n!
Der Beweis des Programms wird von unten nach oben geführt. Wir bezeichnen das gesamte Programm mit X, die While-Schleife mit W und den Schleifenkörper mit S. Zuerst wird die While-Schleife W bewiesen.
Beweis der While-Schleife W
Für den Beweis der While-Schleife beweisen wir die beiden Prämissen der Schlussregel.
Prämisse While1: Nachbedingung R in die Form P ∧ ¬B bringen
Wir bringen die Nachbedingung R, die am Ende der While-Schleife gilt, in die Form P ∧ ¬B. Hierzu ist es erforderlich, in irgendeiner Weise die Bedingung ¬B: i ≥ n und damit die Variable i einzuführen.
| { P ∧ ¬B } | (5) | |
| { f = i! ∧ i ≤ n ∧ i ≥ n } | (4) | |
| { f = i! ∧ i = n } | (3) | |
| { f = n! } | (2) | |
| { R } | (1) |
Aus (4) ergibt sich somit die Schleifeninvariante P, die wir benötigen, um die zweite Prämisse zu beweisen.
P: f = i! ∧ i ≤ n
Prämisse While2: Beweis des Schleifenkörpers S
Wir beweisen nun {P ∧ B} S {P} für den Schleifenkörper S.
Der Beweis wird von unten nach oben geführt:
| { P ∧ B } | (7) | |
 | { f = i! ∧ i ≤ n ∧ i < n } | (6) |
 | { f = i! ∧ i < n } | (5) |
| { f·(i+1) = (i+1)! ∧ i+1 ≤ n } | (4) | |
| i=i+1; | ||
| { f·i = i! ∧ i ≤ n } | (3) | |
| f=f*i; | ||
| { f = i! ∧ i ≤ n } | (2) | |
| { P } | (1) |
Hierbei gilt (5) ⇒ (4), da aus f = i! durch Multiplikation mit i+1 folgt f·(i+1) = (i+1)! und aus i < n folgt i+1 ≤ n. Ferner gilt (6) ⇒ (5), da (6) eine Verschärfung von (5) ist.
Da die beiden Prämissen erfüllt sind, gilt somit aufgrund der Schlussregel für die While-Schleife W folgende Korrektheitsformel:
{ f = i! ∧ i ≤ n } W { f = n! }.
Beweis des gesamten Programms X
Der Rest des Programms wird wie folgt bewiesen:
| { Q } | (7) | |
| { n ≥ 0 } | (6) | |
| { true ∧ 0 ≤ n } | (5) | |
| { 1 = 0! ∧ 0 ≤ n } | (4) | |
| i=0; | ||
| { 1 = i! ∧ i ≤ n } | (3) | |
| f=1; | ||
| { f = i! ∧ i ≤ n } | (2) | |
| { P } | (1) |
Als schwächste Vorbedingung ergibt sich n ≥ 0. Insgesamt gilt also für das gesamte Programm X
| { n ≥ 0 } | |
| X | |
| { f = n! } |
Der schwierigste Schritt bei der formalen Verifikation von While-Schleifen ist das Finden einer geeigneten Schleifeninvariante. Eine gute Hilfe ist das Aufstellen eines Iterationsschemas; dies ist eine Tabelle, die den Werteverlauf der Variablen wiedergibt, die im Schleifenkörper verändert werden. Die Schleifeninvariante lässt sich aus dem Iterationsschema ablesen als eine Bedingung, die für alle Spalten vor und einschließlich derjenigen Spalte gilt, in der das Ergebnis erwartet wird.
Aufgaben
Aufgabe 1: (Rest bei ganzzahliger Division)
Gegeben sei folgendes Programm X mit ganzzahligen Variablen a, b, q und r:
r=a;
while (r>=b)
{
q=q+1;
r=r-b;
}
Das Programm soll den Rest r bei ganzzahliger Division von a durch b berechnen.
Beweisen Sie, dass die Nachbedingung
R: a = q·b + r ∧ r ≥ 0 ∧ r < b
gilt, falls die Schleife terminiert (partielle Korrektheit).
Wie lautet die Schleifeninvariante P? Welches ist die schwächste Vorbedingung Q des Programms?
Aufgabe 2: (Berechnung von n2 mithilfe von Additionen)
Meistens gelingt es, beim Beweis der Prämisse While1 die Schleifeninvariante P zu finden. Bei folgendem Programm ergibt sich P auf diese Weise nicht automatisch.
Gegeben sei folgendes Programm X:
i=0;
q=0;
while (i<n)
{
i=i+1;
k=k+2;
q=q+k;
}
Das Programm X berechnet das Quadrat einer ganzen Zahl n.
Ermitteln Sie die schwächste Vorbedingung Q für die Korrektheitsformel {Q} X {R} mit der Nachbedingung
R: q = n2
Aufgabe 3: Entwickeln Sie eine Schlussregel für die Do-While-Schleife do S while (B);. Welche Prämissen sind für die Schlussregel erforderlich, damit als Konklusion {Q} do S while (B); {R} gilt?
Hinweis: Zeichnen Sie das Flussdiagramm einer Do-While-Schleife und tragen Sie die jeweils geltenden Bedingungen in das Flussdiagramm ein. Vergleichen Sie diese Bedingungen mit den entsprechenden Bedingungen im Flussdiagramm für das äquivalente Programmstück S; while (B) S.
Weiter mit: [Totale Korrektheit] [Literatur] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden