Post-Quanten-Kryptografie
Code-basierte Verschlüsselung
Fehlererkennende und fehlerkorrigierende Codes
Ein Code ist in diesem Zusammenhang eine Menge von Wörtern über 𝔹 = {0, 1}, den Codewörtern. Wenn alle Codewörter eine feste Länge n ∈ ℕ haben, so spricht man von einem Blockcode C ⊆ 𝔹n oder auch einfach von einem n-Bit-Code. Die Codewörter eines Blockcodes lassen sich auch als Vektoren auffassen, also als Elemente des Vektorraums 𝔹n über dem Körper 𝔹 = ℤ2. Die Vektoren werden im Folgenden ähnlich wie Wörter als Zeilenvektoren geschrieben.
Ein Blockcode C der Länge n mit weniger als |𝔹n| = 2n Codewörtern bietet grundsätzlich die Möglichkeit der Fehlererkennung. Solche Fehler sind beispielsweise Übertragungsfehler beim Senden über einen störungsanfälligen Kanal.
Denn beim Senden werden ausschließlich Codewörter gesendet – wird jedoch ein Nicht-Codewort empfangen, so ist ein Fehler aufgetreten und damit erkannt worden. Dies ist das Prinzip der Fehlererkennung bei Codes. Ist ein Fehler erkannt worden, so kann man ihn möglicherweise sogar korrigieren, indem man annimmt, dass das empfangene Wort aus dem "nächstgelegenen" Codewort hervorgegangen ist. Eine wichtige Voraussetzung hierfür ist, dass das "nächstgelegene" Codewort eindeutig ist.
Hamming-Abstand
Der Hamming-Abstand ist ein Maß dafür, wie nahe zwei Wörter beieinanderliegen. Er besagt, an wievielen Positionen sich die Bits dieser Wörter unterscheiden. Um den Hamming-Abstand d(x, y) zweier Wörterx und y ∈ 𝔹n zu bestimmen, schreiben Sie die Wörter untereinander und vergleichen sie Bit für Bit. Technisch führen Sie den Vergleich durch, indem Sie die Bits modulo 2 addieren – kommt 1 heraus, so sind die Bits unterschiedlich, kommt 0 heraus, so sind sie gleich. Oder noch technischer: indem Sie die Wörter als Vektoren auffassen und diese addieren.
Beispiel:
| x | = | 0 1 1 0 1 |
| y | = | 0 0 1 1 1 |
| x ⊕ y | = | 0 1 0 1 0 |
Die Anzahl der Einsen in einem Wort x ∈ 𝔹n wird als das Hamming-Gewicht w(x) des Wortes x bezeichnet. Damit gilt für den Hamming-Abstand
d(x, y) = w(x⊕y)
Der Hamming-Abstand d(C) eines Codes C ist das Minimum aller Hamming-Abstände zwischen je zwei verschiedenen Codewörtern.
Fehlermodell
Die Fehler, die im Folgenden betrachtet werden, entstehen ausschließlich durch "Umkippen" von Bits, also dadurch, dass eine 0 in eine 1 verfälscht wird oder umgekehrt. Nicht betrachtet werden dagegen Fehler, die entstehen, wenn Bits verloren gehen oder sich zusätzlich einschleichen.
Technisch gesehen ist ein Fehler ein Wort e ∈ 𝔹n mit w(e) > 0. Indem Sie e zu einem Codewort x addieren, verfälschen Sie das Codewort. Der Fehler wird erkannt, wenn x ⊕ e ∉ C gilt, wenn also ein Nicht-Codewort herauskommt.
Ein Fehler e heißt Einfachfehler, wenn w(e) = 1, und Doppelfehler, wenn w(e) = 2.
Ein Code C mit Hamming-Abstand d(C) > 1 erkennt alle Einfachfehler. Ein Code C mit d(C) > 2 erkennt alle Doppelfehler usw.
Ein Code C mit d(C) > 2 korrigiert alle Einfachfehler. Allgemein korrigiert ein Code C mit d(C) > 2·k alle k-fach-Fehler.
Die Sprechweise, dass "der Code einen Fehler erkennt bzw. korrigiert" verkürzt die sinnvollere, jedoch umständlichere Ausdrucksweise, dass "der Code die Erkennung bzw. Korrektur eines Fehlers ermöglicht".
Lineare Codes
Ein n-Bit-Code ist ein linearer Code, wenn die Summe zweier Codewörter wieder ein Codewort ergibt. Ein linearer Code bildet einen Teilraum des Vektorraums 𝔹n.
Wir betrachten im Folgenden eine bestimmte Art von linearen Codes, die systematischen (n,k)-Codes. Dies sind n-Bit-Codes, bei denen die ersten k Bits der Codewörter die eigentliche Information enthalten. Die restlichen n-k Bits sind Prüfbits. Die Prüfbits stellen die nötige Redundanz zur Verfügung, die für die Fehlererkennung erforderlich ist.
Beispiel: Der folgende Code C4,3 ist ein (4,3)-Code, der aus 3 Informationsbits und einem Paritätsbit besteht. Das Paritätsbit sorgt dafür, dass alle Codewörter eine gerade Anzahl von Einsen enthalten. Wörter mit ungerader Anzahl von Einsen sind Nicht-Codewörter.
| 0 0 0 0 |
| 0 0 1 1 |
| 0 1 0 1 |
| 0 1 1 0 |
| 1 0 0 1 |
| 1 0 1 0 |
| 1 1 0 0 |
| 1 1 1 1 |
Ein (n,k)-Code enthält 2k Codewörter, er hat als Teilraum von 𝔹n die Dimension k.
Die k Basisvektoren eines (n,k)-Codes untereinander geschrieben bilden eine Generatormatrix G des Codes. So ist beispielsweise
| G = | 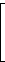 |
| 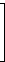 |
eine Generatormatrix des Codes C4,3.
Die Generatormatrix ist nicht eindeutig, da es verschiedene Basisvektoren gibt und deren Reihenfolge als Zeilen der Matrix nicht festgelegt ist. Durch äquivalente Umformungen kann die Generatormatrix in die systematische Form G = [Ik P] gebracht werden, wobei Ik die k×k-Einheitsmatrix ist. P steht für die weiteren n-k Spalten der Matrix. Die Generatormatrix aus dem obigen Beispiel befindet sich bereits in dieser systematischen Form.
Die Generatormatrix G erzeugt den Code C, indem alle Produkte von Vektoren aus 𝔹k und G gebildet werden:
C = { a·G | a ∈ 𝔹k }
Kontrollmatrix
Aus einer systematischen Generatormatrix G = [Ik P] konstruieren Sie in folgender Weise eine Kontrollmatrix H:
H = [PT In-k]
Sie transponieren also den Teil P der systematischen Generatormatrix G und fügen eine (n-k)×(n-k)-Einheitsmatrix an.
Beispiel: Aus der oben angegebenen Generatormatrix G erhalten Sie PT = [1 1 1]. Indem Sie noch die 1×1-Einheitsmatrix [1] anfügen, erhalten Sie die Kontrollmatrix
H = [1 1 1 1]
Fehlererkennung mit der Kontrollmatrix
Satz: Sei C ein (n,k)-Code mit Kontrollmatrix H. Dann gilt für alle Vektoren x ∈ 𝔹n
x ∈ C ⇔ x·HT = 0
Das Produkt x·HT des Vektors x mit der transponierten Kontrollmatrix wird als das Syndrom von x bezeichnet. Ist das Syndrom ungleich 0, so ist ein Fehler aufgetreten.
Bei fehlerkorrigierenden Codes liefert das Syndrom die Information darüber, wie der Fehler zu korrigieren ist. Ein Beispiel hierfür ist der Hamming-Code.
Das Syndrom-Dekodierungs-Problem
Der Hamming-Code ist gerade so konstruiert, dass die Fehlerkorrektur mithilfe des Syndroms einfach ist. Im Allgemeinen jedoch ist die Zuordnung zwischen Syndrom und Fehler schwierig. Dies ist das sogenannte Syndrom-Dekodierungs-Problem.
Das Syndrom-Dekodierungs-Problem machen Sie in folgender Weise für die Kryptografie nutzbar. Grundlage ist ein linearer Code C, dessen Syndrom einfach zu dekodieren ist (wie z.B. der Hamming-Code). Nun machen Sie die Generatormatrix G dieses Codes unkenntlich, indem sie diese mit zwei zufällig erzeugten Matrizen S und P multiplizieren:
G' = S · G · P
Als Empfänger verwenden Sie G' als öffentlichen Schlüssel. Die Matrizen S, G und P bilden Ihren zugehörigen privaten Schlüssel. Ein Syndrom s' von G' ist für einen Angreifer schwer zu dekodieren. Sie hingegen als legitimer Empfänger transformieren s' mithilfe von S und P und können es anschließend einfach dekodieren.
Dies ist die Idee des Verschlüsselungsverfahrens von McEliece, es stammt bereits aus dem Jahr 1978. Damals gab es noch keine Quantencomputer, sondern gerade einmal den 16-Bit-Prozessor Intel 8086 – sicher ein Grund dafür, dass dieses Verfahren seither nicht die Popularität etwa von RSA erfahren hat, denn es ist aufwendiger und schwieriger zu parametrisieren.
McEliece-Verschlüsselung
Gegeben ist die Generatormatrix G eines linearen (n,k)-Codes mit Hamming-Abstand h und eine zugehörige Syndrom-Dekodierungs-Funktion.
Schlüssel erzeugen
Ausgabe:
Öffentlicher Schlüssel G' und privater Schlüssel (S, G, P)
Methode:
- Erzeuge eine zufällige, invertierbare k×k-Matrix S
- Erzeuge eine zufällige n×n-Permutationsmatrix P
- Berechne G' = S · G · P
- Gib G' als öffentlichen Schlüssel und (S, G, P) als privaten Schlüssel zurück
Verschlüsseln
Eingabe:
Öffentlicher Schlüssel G' und Klartext m ∈ 𝔹n
Ausgabe:
Geheimtext c
Methode:
- Erzeuge einen zufälligen n-Bit-Vektor e mit Hamming-Gewicht w(e) = (h-1) div 2
- Berechne c = m · G' + e
- Gib den Geheimtext c zurück
Entschlüsseln
Eingabe:
Privater Schlüssel (S, G, P) und Geheimtext c
Ausgabe:
Klartext m ∈ 𝔹n
Methode:
- Berechne u = c · P-1
- Berechne das Syndrom s' = u · HT
- Dekodiere aus s' den zugehörigen Fehlervektor e'
- Berechne v' = u + e' und berücksichtige nur die Informationsbits, also die ersten k Bits von v' und erhalte so v
- Berechne m = v · S-1
Beispiel mit kleinen Zahlen
Gegeben ist ein linearer (7,4)-Code C mit 4×7-Generatormatrix
| G = | 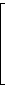 |
| 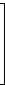 |
und die zugehörige 3×7-Kontrollmatrix
| H = | 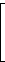 |
| 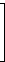 |
Der Code hat den Hamming-Abstand d(C) = 3.
Schlüssel erzeugen
In Schritt 1 erzeugen Sie eine zufällige, invertierbare 4×4-Matrix
| S = | 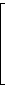 |
| 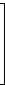 |
In Schritt 2 erzeugen Sie eine zufällige 7×7-Permutationsmatrix
| P = |  |
|  |
In Schritt 3 berechnen Sie G' = S · G · P
| G' = | 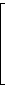 |
| 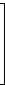 |
Sie geben nun den öffentlichen Schlüssel G' und den privaten Schlüssel (S, G, P) zurück.
Verschlüsseln
Als Eingabe verwenden Sie den öffentlichen Schlüssel G' des Empfängers sowie einen Klartext der Länge 4, also z.B. m = [1 0 1 1].
In Schritt 1 erzeugen Sie einen zufälligen n-Bit-Vektor e mit Hamming-Gewicht w(e) = (h-1) div 2 = 1:
e = [0 0 1 0 0 0 0]
In Schritt 2 berechnen Sie c = m · G' + e =
| [ 1 0 1 1 ] | · |
| + | [ 0 0 1 0 0 0 0 ] | = | [ 0 1 0 0 1 1 0 ] |
Zum Schluss geben Sie den Geheimtext c = [0 1 0 0 1 1 0] zurück.
Entschlüsseln
Als Eingabe verwenden Sie Ihren privaten Schlüssel (S, G, P) sowie den Geheimtext c.
In Schritt 1 berechnen Sie u = c · P-1 =
| [ 0 1 0 0 1 1 0 ] | · |
| = | [ 0 0 0 1 1 0 1 ] |
Für eine Permutationsmatrix P gilt P-1 = PT.
In Schritt 2 berechnen Sie s' = u · HT =
| [ 0 0 0 1 1 0 1 ] | · |
| = | [ 0 1 0 ] |
In Schritt 3 dekodieren Sie das Syndrom s', d.h. Sie suchen den zugehörigen Fehlervektor e'. Dieser ist
e' = [0 0 0 0 0 1 0] (denn e' · HT = s')
In Schritt 4 korrigieren Sie das Zwischenergebnis u, indem Sie den Fehlervektor e' addieren:
v' = u + e' = [0 0 0 1 1 0 1] + [0 0 0 0 0 1 0] = [0 0 0 1 1 1 1]
Von v' berücksichtigen Sie nur die Informationsbits, also die ersten 4 Bits, und erhalten
v = [0 0 0 1]
In Schritt 5 schließlich machen Sie S rückgängig durch m = v · S-1 =
| [ 0 0 0 1 ] | · |
| = | [ 1 0 1 1 ] |
Wie gewünscht haben Sie den ursprünglichen Klartext m zurückerhalten.
Literatur
Die hier gewählte Darstellung folgt dem Buch
[PPG 24] C. Paar, J. Pelzl, T. Güneysu: Understanding Crytography. 2. Auflage, Springer (2024)
Weiter mit: [Dilithium-Signaturverfahren] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 17.06.2025 Updated: 25.06.2025
Diese Webseiten sind größtenteils während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden