Post-Quanten-Kryptografie

Dilithium-Signaturverfahren

Zum Verständnis des Dilithium-Signatur­verfahrens ist es hilfreich, wenn Sie sich zunächst das Signatur­verfahren von Schnorr noch einmal ansehen.

Signaturverfahren von Schnorr

Vorgegeben ist eine zyklische Gruppe G der Ordnung n, ein festgelegtes erzeugendes Element g und eine Hashfunktion H.

 

Schlüssel erzeugen

Ausgabe:

Öffentlicher Schlüssel ga und privater Schlüssel a

Methode:

  1. Wähle zufällig eine Zahl a ∈ {2, ..., n-2}
  2. Berechne ga in der Gruppe G
  3. Gib ga als öffentlichen Schlüssel und a als privaten Schlüssel zurück

 

 

Signieren

Eingabe:

Dokument m ∈ {0, 1}*, privater Schlüssel a

Ausgabe:

Signatur s

Methode:

  1. Wähle zufällig eine Zahl y ∈ {2, ..., n-2}
  2. Berechne w = gy in der Gruppe G   (commitment - Festlegung)
  3. Berechne c  =  H(m||w)   (challenge - Abfrage)
  4. Berechne z  =  y + ca mod n   (response - Auf­lösung)
  5. Gib die Signatur s = (c, z) zurück

 

Die Operation || bedeutet hier Verkettung.

 

Signatur prüfen

Eingabe:

Dokument m, Signatur s = (c, z), öffentlicher Schlüssel ga

Methode:

  1. Berechne w' = gz·(ga)-c in der Gruppe G
  2. Akzeptiere, falls c = H(m||w')

 

Bemerkungen

Die Prüfung der Signatur funktioniert, denn es ist

y  =  z – ca mod n

und damit

w'   =   gz·(ga)-c   =   gz·g-ca   =   gz-ca   =   gy   =   w

 

Die Reduktion modulo n in Schritt 3 ist möglich, da n die Ordnung der Gruppe G ist und damit gn = 1 ist. Somit ist

gca mod n   =   gca-kn   =   gca · g-kn   =   gca · (gn)-k   =   gca · 1-k   =   gca

 

Die Sicherheit dieses Signatur­verfahrens beruht auf der Schwierig­keit, das Diskrete-Logarithmus-Problems (DLP) zu lösen. Ein Angreifer kann keine gültige Signatur erstellen, ohne die Zahl a zu kennen, auch dann nicht, wenn er z kennt.

Dilithium

Notation

Sie kennen die Operation mod n, die den Rest bei Division durch n liefert. Hierbei liegt dieser Rest zwischen 0 und n-1. Die Operation mods n liefert ebenfalls den Rest bei Division durch n, wobei dieser Rest jedoch zwischen -(n-1) div 2 und n div 2 liegt.

Zum Beispiel liegt der Rest

Sie inter­pretieren also den Rest als negative Zahl, wenn er größer als n div 2 ist.

Definition:  (Operation mods)

Für alle Zahlen a ∈ ℤ und n ∈ ℕ, n > 1 ist

a mods n  =   geschweifte Klammer
a mod n    falls a mod n ≤ n div 2
a mod n – n    sonst

Im Dilithium-Signatur­verfahren spielen folgende Mengen eine Rolle:

ℤq  =  {0, ..., q-1}
Rq=ℤq[x] / (xn +1)
Sη=Teilmenge von Rq, Polynome mit Koeffizienten (mods q) in {-η, ..., η}
S'γ1=Teilmenge von Rq, Polynome mit Koeffizienten (mods q) in {-γ1+1, ..., γ1}

Im Dilithium-Standard ML-DSA-87 haben die dabei auf­tretenden Parameter folgende Werte:

q = 223 – 213 +1  =  8.380.417 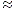 ungefähr gleich  223
n=256
(k, l)=(8, 7)
η=2
γ1=219
Verfahren

Das Dilithium-Signatur­verfahren basiert auf Matrizen und Vektoren, deren Komponenten Polynome aus Rq sind. So ist etwa Rqk×l die Menge aller k×l-Matrizen mit Komponenten aus Rq. Und Sηk ist die Menge aller Vektoren der Länge k mit Komponenten aus der Menge Sη.

 

Schlüssel erzeugen

Ausgabe:

Öffentlicher Schlüssel (A, t) und privater Schlüssel (s1, s2)

Methode:

  1. Wähle zufällig eine k×l-Matrix A ∈ Rqk×l
  2. Wähle zufällig einen Vektor s1 ∈ Sηl der Länge l
  3. Wähle zufällig einen Vektor s2 ∈ Sηk der Länge k
  4. Berechne  t  =  A·s1 + s2
  5. Gib (A, t) als öffentlichen Schlüssel und (s1, s2) als privaten Schlüssel zurück

 

 

Signieren

Eingabe:

Dokument m ∈ {0, 1}*, privater Schlüssel (s1, s2)

Ausgabe:

Signatur s

Methode:

  1. Wähle zufällig einen Vektor y ∈ S'γ1l der Länge l
  2. Berechne w = A·y
  3. Berechne c  =  H(m||w)
  4. Berechne z  =  y + c·s1
  5. Gib die Signatur s = (c, z) zurück

 

Hierbei sind  w ∈ Rqk,  z ∈ Rql,  c ∈ Rq. Die Operation || bedeutet Verkettung.

 

Signatur prüfen

Eingabe:

Dokument m, Signatur s = (c, z), öffentlicher Schlüssel (A, t)

Methode:

  1. Berechne w'   (siehe Text unten)
  2. Akzeptiere, falls c  =  H(m||w')

 

Problem

Es ist z = y + c·s1, durch Multi­plikation mit A ergibt sich

A·z   =   A·y + c·(A·s1)   =   w + c·(t – s2)   =   w + c·t – c·s2

Also ist

A·z – c·t  =  w – c·s2

Um die Signatur zu prüfen, ist es nicht möglich, w' direkt zu berechnen, sondern zunächst nur w' – c·s2.

Lösung

Zum Glück hat das Polynom c·s2 nur kleine Koeffizienten, denn sowohl c als auch s2 haben kleine Koeffizienten. Die Idee zur Lösung des Problems besteht darin, nur die HighBits, also die höchstsignifikanten Bits der Koeffizienten der Polynome zu betrachten.

Um dies zu erreichen, wird die Abfrage (challenge) nur mit den HighBits von w erzeugt. Mit w1 = HighBits(w) ergibt sich nun

c  = H(m||w1).

Wenn die LowBits von w – c·s2 klein genug sind, ergibt sich somit

HighBits(w – c·s2)  =  HighBits(w)

In diesem Fall gilt

w1'   =   HighBits(A·z – c·t)   =   HighBits(w – c·s2)   =   HighBits(w)   =   w1

Modifikation der Signatur-Erzeugung und -Prüfung

 

Signieren (modifiziert)

Eingabe:

Dokument m ∈ {0, 1}*, privater Schlüssel (s1, s2)

Ausgabe:

Signatur s

Methode:

  1. Wiederhole
      1. Wähle zufällig einen Vektor y ∈ S'γ1l der Länge l
      2. Berechne w = A·y  und  setze w1 = HighBits(w)
      3. Berechne c  =  H(m||w1)
      4. Berechne z  =  y + c·s1
  2. solange LowBits(w – c·s1) nicht klein genug
  3. Gib die Signatur s = (c, z) zurück

 

 

Signatur prüfen (modifiziert)

Eingabe:

Dokument m, Signatur s = (c, z), öffentlicher Schlüssel (A, t)

Methode:

  1. Berechne w1'  =  HighBits(A·z – c·t)
  2. Akzeptiere, falls c  =  H(m||w1')

 

Bewertung und Optimierungen

Die Sicherheit des Dilithium-Signatur­verfahrens beruht auf der Schwierig­keit, das MLWE-Problem (Module Learning With Errors) zu lösen.

Der Aufwand des Verfahrens ist zunächst hoch, mit q 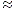ungefähr gleich 223 umfasst die Matrix A eine Datenmenge von 56·256·23 Bit 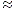ungefähr gleich 40 KByte und der Vektor t immerhin auch noch einmal 8·256·23 Bit 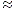ungefähr gleich 6 KByte.

Eine mögliche Lösung ist, nur den Startwert (seed) σ für einen vorgegebenen Zufallsbit-Generator zu ver­öffentlichen, d.h. der öffentliche Schlüssel ist nun (σ, t). Des Weiteren genügt es, nur die HighBits von t zu ver­öffentlichen.

Auch ist es aufwendig, in jeder Iteration der modifizierten Signatur-Erzeugung den Hashwert eines möglicher­weise sehr großen Dokuments m zu berechnen. Daher wird zunächst μ = H(m) berechnet und dann in jeder Iteration nur noch c = H(μ||w1).

 

Dies sind nur die Grundzüge des Dilithium-Signatur­verfahrens. Das komplette Verfahren ist quite involved (ziemlich verwickelt); es ist als ML-DSA (Module-Lattice-Based Digital Signature Algorithm) in FIPS 204 der NIST ver­öffentlicht.

Literatur

Die hier gewählte Darstellung folgt dem Video von A. Menezes:

[Web 1]   https://www.youtube.com/watch?v=DCtwD_mN680  

Der Standard der NIST ist hier ver­öffentlicht:

[FIPS 204]   https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.204.pdf

 

Weiter mit:   [up]

 

H.W. Lang   mail@hwlang.de   Impressum   Datenschutz
Created: 24.06.2025   Updated: 26.06.2025
Diese Webseiten sind größtenteils während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden