Codierungstheorie
Hamming-Code
Hamming-Codes (nach R.W. Hamming ) sind lineare (n, k)-Codes mit dem Hamming-Abstand 3; mit ihnen lassen sich also Einfachfehler korrigieren [Ham 50].
) sind lineare (n, k)-Codes mit dem Hamming-Abstand 3; mit ihnen lassen sich also Einfachfehler korrigieren [Ham 50].
Idee
Die Idee, die der Konstruktion von Hamming-Codes zugrunde liegt, lässt sich auf zwei unterschiedliche Weisen vermitteln. Die eine Möglichkeit beruht auf den algebraischen Eigenschaften von linearen Codes, mit dieser beginnen wir im Folgenden. Alternativ dazu ist die Konstruktion durch überlappende Paritätsprüfungen möglich.
Ein n-Bit-Hamming-Code ist ein linearer Code, der als Kontrollmatrix H eine Matrix verwendet, deren j-ter Spaltenvektor die Binärdarstellung der Zahl j enthält (j ∈ {1, ..., n}).
Beispiel: Es sei n = 5. Dann ist die Kontrollmatrix
| H = | 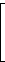 |
| 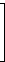 |
Die j-te Spalte von H enthält jeweils die Binärdarstellung von j.
Sei nun c ∈ 𝔹n ein Codewort des Hamming-Codes, das durch einen Einfachfehler e ∈ 𝔹n in ein Wort x ∈ 𝔹n verfälscht worden ist:
x = c⊕e
Dann liefert das Syndrom x·HT genau die Position (in Binärdarstellung) des Einfachfehlers. Denn es ist
| x · HT | = | (c⊕e) · HT | ||
| = | c · HT ⊕ e · HT | |||
| = | e · HT |
Da der Einfachfehler e an genau einer Stelle j eine 1 hat, ergibt e · HT die j-te Spalte von H, und diese enthält die Binärdarstellung von j.
Der Einfachfehler lässt sich somit korrigieren, indem das j-te Bit von x invertiert wird.
Beispiel: Es ist
[1 1 1 0 1] · HT = [1 0 1]
d.h. an Position 5 ist ein Fehler aufgetreten. Das richtige Codewort wäre 1 1 1 0 0 gewesen.
Konstruktion des Hamming-Codes
Ist die Kontrollmatrix H in der obigen Form gegeben, so lässt sich der zugehörige Hamming-Code durch Umkehrung des im Kapitel Lineare Codes beschriebenen Verfahrens konstruieren.
Zunächst wird die Kontrollmatrix H durch Spaltenvertauschungen (repräsentiert durch die Permutationsmatrix S) in die Form
H' = H · S = [PT In-k]
gebracht.
Aus H' wird G' konstruiert:
G' = [Ik P],
und durch Rückgängigmachen der Spaltenvertauschungen wird aus G' eine Generatormatrix des Hamming-Codes erzeugt:
G = G' · ST.
Beispiel: Gegeben sei die Kontrollmatrix H aus dem vorigen Beispiel.
| H = | 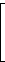 |
| 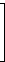 |
Durch Spaltenvertauschungen ergibt sich
| H' = [PT I3] = | 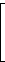 |
| 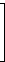 |
Damit ist
| G' = [I2 P] = | 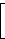 |
| 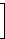 |
und durch Rückgängigmachen der Spaltenvertauschungen ergibt sich die Generatormatrix G des Hamming-Codes:
| G = | 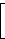 |
| 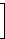 |
Der erzeugte Hamming-Code ist ein (5,2)-Code, d.h. ein Code mit 5 Bit Codewortlänge, bestehend aus 2 Informations- und 3 Prüfbits.
Perfekte Hamming-Codes
Statt nur 2 Informationsbits wie im vorigen Beispiel wären auch 4 Informationsbits möglich gewesen. Hierzu ist die Kontrollmatrix um zwei weitere Spalten mit den Binärdarstellungen von 6 und 7 zu erweitern und anschließend das Konstruktionsverfahren durchzuführen. Das Ergebnis ist ein (7,4)-Code, also ein Code mit 7 Bit Codewortlänge, davon 4 Informationsbits und 3 Prüfbits.
Dieser (7,4)-Hamming-Code hat folgende Kontrollmatrix H und Generatormatrix G:
| H = | 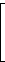 |
| 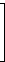 |
| G = | 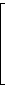 |
| 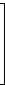 |
Der (7,4)-Hamming-Code ist ein perfekter Code, da er für die Codewortlänge 7 und den vorgegebenen Hamming-Abstand 3 die maximal mögliche Anzahl von Codewörtern enthält.
Allgemein gibt es perfekte (n, k)-Hamming-Codes mit n = 2m-1, wobei m ∈ ℕ die Anzahl der Prüfbits und k = n-m die Anzahl der Informationsbits sind. Dies sind also (1,0)-, (3,1)-, (7,4)-, (15,11)-, (31,26)-Hamming-Codes usw. 1)
Alternative Konstruktion des Hamming-Codes
Die Multiplikation eines Wortes x ∈ 𝔹n mit einer Spalte von HT (d.h. mit einer Zeile von H) entspricht einer Paritätsprüfung in denjenigem Teilbereich des Wortes x, in dem die Zeile von H Einsen hat.
Im Falle der Kontrollmatrix H des (7,4)-Hamming-Codes kommen hierdurch drei einander überlappende Paritätsprüfungen zustande (blau, grün und gelb gekennzeichnete Bereiche in Bild 1). Bei Codewörtern muss die Parität in allen diesen Bereichen 0 sein. Ist die Parität in einem oder mehreren Bereichen verletzt, lässt sich die Position des Fehlers aufgrund der Überlappungen der Bereiche eindeutig bestimmen.
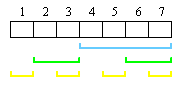
Bild 1: Bereiche mit Parität 0 in einem Codewort
Um ein Codewort zu konstruieren, werden zunächst die Bitpositionen 2i des Wortes für Paritätsbits reserviert. Dann werden die restlichen Positionen beliebig mit Informationsbits belegt. Anschließend wird jedes Paritätsbit so gesetzt, dass der Bereich, dem es angehört, die Parität 0 erhält.
In folgendem Bild ist ein Beispiel eines 7-Bit-Codewortes zu sehen. Die Paritätsbits stehen an den Positionen 1, 2 und 4 des Wortes. Die restlichen Positionen sind mit Datenbits belegt. Die Paritätsbits sind so gewählt, dass der blaue, der grüne und der gelbe Bereich die Parität 0 haben.
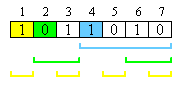
Bild 2: Belegung der Paritätsbits (farbig hinterlegt)
Literatur
[Ham 50] R.W. Hamming: Error Detection and Error Correction Codes. The Bell System Technical Journal, Vol. XXVI, 2, 147-160 (1950)
[Wit 01] K.U. Witt: Algebraische Grundlagen der Informatik. Vieweg (2001)
1) Der (1,0)-Code, der nur aus einem Prüfbit und null Informationsbits besteht, ist natürlich wenig sinnvoll.
Weiter mit: [CRC-Verfahren] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 10.10.2003 Updated: 08.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden