Zahlentheoretische Grundlagen der Kryptografie
Elliptische Kurven
Wir betrachten elliptische Kurven zunächst in der Ebene des ℝ2. Für die kryptografische Anwendung wird später der Körper ℝ durch den endlichen Körper ℤn ersetzt.1) Die hier gewählte Darstellung lehnt sich an [SSP 08] an.
Definition: Eine elliptische Kurve ist eine Menge von Punkten (x, y) in der Ebene, die folgender Gleichung genügen:
E = { (x, y) | y2 = x3 + ax + b } ∪ {u}
Die Parameter a und b sind reelle Zahlen. Der Punkt u ist ein unendlich ferner Punkt.
In Bild 1 ist eine typische elliptische Kurve in der Gegend rund um den Nullpunkt des Koordinatensystems dargestellt.
Verknüpfung von Punkten von E
Auf der Menge E der Punkte einer elliptischen Kurve wird in folgender Weise eine Verknüpfung definiert. Zwei Punkte p und q werden verknüpft, indem eine Gerade g durch p und q gelegt wird. Diese Gerade schneidet die Kurve E in einem dritten Punkt s. Dieser Punkt s wird an der x-Achse gespiegelt, der hierdurch entstehende Punkt r ist das Ergebnis der Verknüpfung:
p • q = r
Man beachte, dass r wieder ein Punkt der Kurve ist, weil diese symmetrisch zur x-Achse verläuft (Bild 1).
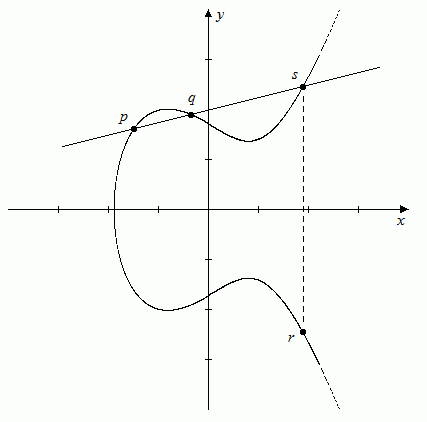
Bild 1: Schnittpunkte einer Geraden mit einer elliptischen Kurve
Einige Sonderfälle sind zu betrachten.
Wenn p = q ist, so ist die Gerade durch p und q die Tangente an die Kurve E im Punkt p. Bei Tangenten zählt der Berührpunkt als Zweifachpunkt, sodass die Gerade und die Kurve auch in diesem Fall drei Punkte gemeinsam haben. Bei der Tangente durch einen Wendepunkt der Kurve zählt der Wendepunkt sogar als Dreifachpunkt.
Wenn einer der Punkte der unendlich ferne Punkt u ist, so ist das Ergebnis der Verknüpfung der andere Punkt. D.h. es gilt für alle Punkte p ∈ E
p • u = u • p = p
Wenn die Punkte p und q an der x-Achse gespiegelt zueinander liegen, so verläuft die Gerade g parallel zur y-Achse. Dann ist der dritte Schnittpunkt s der unendlich ferne Punkt u. Der unendlich ferne Punkt u, an der x-Achse gespiegelt, ergibt wiederum den unendlich fernen Punkt u.
Gruppenstruktur von E
Die Menge E bildet zusammen mit der oben definierten Verknüpfung • eine abelsche Gruppe.
Die Verknüpfung ist also assoziativ. Das neutrale Element der Gruppe ist der unendlich ferne Punkt u. Jeder Punkt p hat ein inverses Element p-1, dies ist der an der x-Achse gespiegelte Punkt, denn es gilt p • p-1 = u. Und schließlich ist die Verknüpfung sogar kommutativ, denn die Gerade durch p und q ist gleich der Geraden durch q und p, der dritte Schnittpunkt s ist somit derselbe.
Berechnung des Schnittpunktes s
Wir setzen zunächst der Einfachheit halber voraus, dass keiner der angegebenen Sonderfälle vorliegt, d.h. wir setzen voraus, dass die x-Koordinaten der beiden Punkte p und q verschieden sind.
Eine Gerade g ist die Menge aller Punkte (x, y), die der Geradengleichung y = mx + c genügen:
g = { (x, y) | y = mx + c }
Hierbei ist m die Steigung der Geraden, c ist der y-Achsenabschnitt.
Die Schnittpunkte der Geraden g mit der elliptischen Kurve E liegen im Durchschnitt der entsprechenden Punktmengen; für die Schnittpunkte gelten also jeweils beide Gleichungen. Durch Einsetzen von
y = mx + c
in die Gleichung von E ergibt sich
(mx + c)2 = x3 + ax + b
bzw. ausmultipliziert und geordnet
-x3 + m2x2 + (2mc – a)x + c2 – b = 0
Zwei der Lösungen dieser Gleichung sind bekannt, nämlich xp und xq, die x-Koordinaten der Punkte p und q. Gesucht ist xs, die x-Koordinate des dritten Schnittpunktes s.
Allgemein gilt für die drei Nullstellen xp, xq und xs eines Polynoms 3. Grades
d(x – xp)(x – xq)(x – xs) = 0
Durch Ausmultiplizieren und Koeffizientenvergleich mit der obigen Gleichung ergibt sich
d = -1 und
m2 = xp + xq + xs
Somit gilt für die x-Koordinate des dritten Schnittpunktes s
xs = m2 – xp – xq
Die Steigung m der Geraden lässt sich mithilfe der beiden Punkte p und q berechnen:
| yp – yq |
| xp – xq |
Mithilfe der Formel für die Steigung lässt sich auch die y-Koordinate des Punktes s bestimmen:
ys = m(xs – xp) + yp
Sonderfälle
Wenn die Punkte p und q an der x-Achse gespiegelt zueinander liegen, d.h. wenn die x-Koordinaten gleich sind und die y-Koordinaten zueinander negativ sind, so verläuft die Gerade g durch p und q parallel zur y-Achse. Der dritte Schnittpunkt mit der elliptischen Kurve ist dann der unendlich ferne Punkt u.
Wenn die Punkte p und q gleich sind, so ist die Gerade g die Tangente an die elliptische Kurve im Punkt p. Die Steigung m der Tangente ergibt sich aus den partiellen Ableitungen der Gleichung der elliptischen Kurve E im Punkt p:
| 3xp2 + a |
| 2yp |
Formel für die Verknüpfung
Unter Berücksichtigung der Sonderfälle ergibt sich somit folgende Berechnungsvorschrift für die Verknüpfung zweier Punkte p und q der elliptischen Kurve E:
| p • q = | 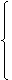 |
|
Zu beachten ist außerdem, dass die Steigung m der Geraden auf unterschiedliche Weise berechnet wird, je nach dem, ob die Punkte p und q gleich oder verschieden sind.
Elliptische Kurven über endlichen Körpern
Alle gezeigten Berechnungen lassen sich statt im Körper ℝ der reellen Zahlen auch in anderen Körpern durchführen. In der Kryptografie wird der endliche Körper ℤn verwendet, wobei n eine Primzahl mit n > 3 ist. Der Körper ℤn besteht aus den ganzen Zahlen {0, ..., n-1}, Addition und Multiplikation werden modulo n durchgeführt.
Da ℤn eine endliche Menge ist, besteht die elliptische Kurve als Teilmenge von ℤn2 auch nur aus endlich vielen Punkten. Bild 2 zeigt die Punkte der elliptischen Kurve y2 = x3 – 2x + 3 über dem Körper ℤ23.

Bild 2: Elliptische Kurve über ℤ23
Die Punkte einer elliptischen Kurve über einem endlichen Körper bilden keine zusammenhängende Linie. Dennoch bleibt die Anschaulichkeit der Verknüpfung von zwei Punkten p und q erhalten: Eine Gerade, die durch zwei Punkte der elliptischen Kurve gezogen wird, erreicht irgendwann einen dritten Punkt der elliptischen Kurve. Gegebenenfalls wird die Gerade, wenn sie das Bild am linken, rechten, oberen oder unteren Rand verlässt, am gegenüber liegenden Rand wieder hereingeführt. Dies ist durch die Modulo-Rechnung bedingt, denn z.B. lassen sich bei n = 23 die Ränder x = -11 und x = 12 miteinander identifizieren, da -11 ≡ 12 (mod 23) gilt.
Die Berechnungsvorschrift für die Verknüpfung von Punkten bleibt ebenfalls gültig. Zu beachten ist nur, dass bei der Berechnung der Steigung m einer Tangente der Teilausdruck 2yp durch yp + yp ersetzt werden muss, da eine Multiplikation der reellen Zahl 2 mit einem Element der Menge ℤn nicht definiert ist. Entsprechendes gilt für den Teilausdruck 3xp2.
Anwendung in der Kryptografie
Wird ein Punkt g auf einer elliptischen Kurve E über ℤn gewählt und v-mal mit sich selbst verknüpft, so lässt sich aus dem Ergebnis q = gv nicht auf v zurückschließen (Problem des diskreten Logarithmus elliptischer Kurven – Elliptic Curve Discrete Logarithm Problem ECDLP). Voraussetzung ist natürlich, dass die beteiligten Zahlen n und v sehr groß sind, sodass es zu lange dauert, die Lösung durch Ausprobieren herauszufinden.
Diese Tatsache wird beispielsweise bei der Diffie-Hellman-Schlüsselvereinbarung ausgenutzt.
Implementierung
In der Implementierung in der Programmiersprache Python dient die Klasse EcPoint zur Darstellung von Punkten auf der elliptischen Kurve. Die Methode __mul__ dient zur Verknüpfung zweier Punkte; sie überschreibt den Operator *, sodass mit der Anweisung r = p*q das Ergebnis r der Verknüpfung zweier Punkte p und q berechnet wird. Die Methode __pow__ überschreibt den Exponentiations-Operator **; sie ist als schnelle Exponentiation mittels Square-and-Multiply implementiert.
Je nach dem, ob der Parameter a und die Koordinaten der Punkte der elliptischen Kurve als Elemente des Körpers ℝ der reellen Zahlen oder als Elemente eines Körpers ℤn angegeben werden, rechnet das Programm mit den Rechenoperationen des entsprechenden Körpers.
Hierzu ist es erforderlich, eine Klasse ModInt zur Repräsentation von Elementen des Körpers ℤn vorzusehen, in der die Rechenoperatoren +, -, * und / entsprechend definiert sind. Dies geschieht, indem mit Methoden __add__, __sub__, __mul__ und __div__ die entsprechenden Rechenoperatoren überschrieben werden.
Literatur
[SSP 08] J. Swoboda, S. Spitz, M. Pramateftakis: Kryptographie und IT-Sicherheit. Vieweg+Teubner (2008)
[Lan 23] H.W. Lang: Kryptografie für Dummies. 2. Auflage, Wiley (2023)
1) Wenn n eine Primzahl ist, bildet die Menge ℤn einen Körper. Üblich sind in diesem Fall auch die Bezeichnungen 𝔽n oder GF(n).
Weiter mit: [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 10.03.2011 Updated: 06.04.2025
Diese Webseiten sind größtenteils während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden
