Berechnungsverfahren
Modulare Exponentiation - rekursive Implementierung
Die modulare Exponentiation spielt allgemein in der Kryptografie eine große Rolle. Im RSA-Verfahren beispielsweise besteht die Chiffrierung in der Berechnung von me mod n. Hierbei sind m, e und n sehr große Zahlen (typischerweise 512 oder 1024 Bit lang).
Um me mod n zu berechnen, sind zum Glück nicht e Multiplikationen von m mit sich selbst erforderlich. Schon bei einer Länge von e von nur 50 Bit wären dies eine Billiarde Multiplikationen. Tatsächlich genügen weniger als 2 log(e) Multiplikationen, also weniger als 100 bei einem 50-Bit-Exponenten.
Für die schnelle modulare Exponentiation (square and multiply) gibt es eine iterative Implementierung unter Benutzung der Binärdarstellung des Exponenten,
Am einfachsten ist die im Folgenden dargestellte rekursive Implementierung; in diesem Fall wird die Binärdarstellung des Exponenten nicht explizit benötigt.
Idee
Ausgehend von der Beobachtung, dass z.B. m13 dargestellt werden kann als
m13 = m12 · m
und m12 als
m12 = (m6)2
lassen sich folgende Rekursionsformeln für die Berechnung von me mit e ∈ ℕ0 aufstellen:
| me = | 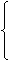 |
|
Programm
Das folgende Python-Programm stellt eine mögliche Implementierung dieser Rekursionsformeln für die modulare Exponentiation dar.
def modexp(m, e, n):
if e==0:
return 1
if e%2==1:
return modexp(m, e-1, n)*m % n
else:
return modexp(m, e//2, n)**2 % n
Eine entsprechende Implementierung in der funktionalen Programmiersprache Haskell ist die folgende:
modexp :: Integer -> Integer -> Integer -> Integer
modexp m e n | e==0 = 1
| odd e = modexp m (e-1) n * m `mod` n
| otherwise = modexp m (e `div` 2) n ^ 2 `mod` n
Weiter mit: [Modulare Exponentiation iterativ] [Primzahltest] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 12.06.2001 Updated: 17.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden