Sorting on two dimensional processor arrays
Sorting algorithm of Schnorr and Shamir
The algorithm 3n-sort of Schnorr and Shamir [SchSh 86] is more complicated than e.g. rotatesort or 4-way mergesort. However, with a time complexity of 3n + o(n) it is optimal, since 3n is a lower bound for sorting on a two-dimensional processor array.
Algorithm
The n×n-array is decomposed into vertical slices, horizontal slices, and blocks. A vertical slice is an n×n3/4-subarray, a horizontal slice is an n3/4×n-subarray, and a block is an n3/4×n3/4-subarray (Figure 1).
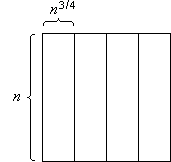
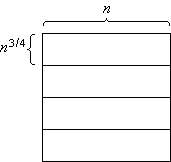
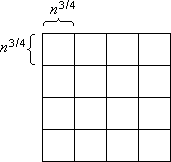
Figure 1: Vertical slices (a), horizontal slices (b) and blocks (c)
The entire array as well as subarrays (blocks, slices) are sorted in snake-like order.
The algorithm of Schnorr/Shamir uses the following operation unshuffle.
unshuffle
A k-way unshuffle operation is a permutation that corresponds to dealing n cards to k players (k is a divisor of n).
Example: Permutation 4-way unshuffle of the numbers 0, ..., 11
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 0 | 4 | 8 | 1 | 5 | 9 | 2 | 6 | 10 | 3 | 7 | 11 |
Player 1 receives cards 0, 4 and 8, player 2 receives cards 1, 5 and 9 etc.
In algorithm 3n-sort an n1/4-way unshuffle of the elements of the rows is performed.
Algorithm 3n-sort
Input:
unsorted n×n-array of data
Output:
the sorted n×n-array
Method:
- sort the blocks;
- n1/4-way unshuffle along the rows;
- sort the blocks;
- sort the columns;
- sort the vertical slices;
- sort the rows in alternating direction;
- apply n3/4 steps of odd-even transposition sort to the snake;
Sorting in alternating direction means to sort each row i with i even into ascending order, and each row i with i odd into descending order (i ∈ {0, ..., n-1}).
Correctness
The correctness of 3n-sort is shown again (in a slightly different way as in [SchSh 86]) using the 0-1-principle. In the following figures zeroes are drawn white and ones gray.
Definition: A row is called clean, if it consists of zeroes or ones only, otherwise it is called dirty. A dirty row in a sorted array is called incomplete.
Definition: The number of ones in an r × s-subarray is called the weight of the subarray.
In particular, this definition refers to columns and blocks.
Definition: A maximal connected region along the sorting order that starts with a one and ends with a zero is called an unsorted zone.
A sequence containing an unsorted zone starts with some 0's, then comes a mix of 1's and 0's, and then may come 1's.
Step 1
After sorting the blocks each block has at most one incomplete row (Figure 2a).
Step 2
The operation n1/4-way unshuffle distributes the columns of a block to all n1/4 blocks of the same horizontal slice in a round-robin way. If a block has an incomplete row, some blocks receive a one more from this block than others. Altogether, a block can receive at most n1/4 ones more than any other, i.e. the weights of any two blocks in a horizontal slice can differ by at most n1/4 (Figure 2b).
Step 3
After sorting the blocks again each block contains at most one incomplete row (Figure 2c).
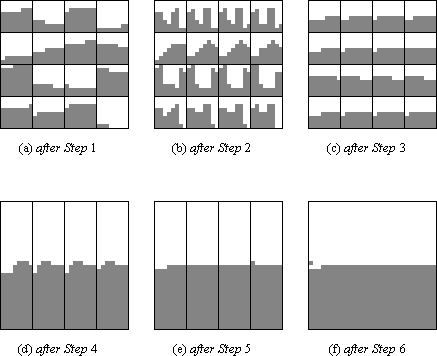
Figure 2: Situations during the execution of the algorithm
Step 4
After sorting the columns each vertical slice has at most n1/4 dirty rows (the incomplete rows of its n1/4 blocks).
Moreover, the weights of any two vertical slices differ by at most n1/4 · n1/4 = n1/2 (Figure 2d).
Step 5
After sorting the vertical slices all vertical slices have almost the same number of complete 1-rows: the difference can be at most 1. Since vertical slices have a width of n3/4, a weight difference of n1/2 can contribute to at most one additional complete 1-row.
The region of length n1/2 on the snake in each vertical slice that can contain these additional ones is called the critical region (drawn in red in Figure 3a, not in correct scale).
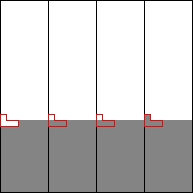
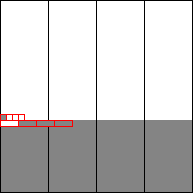
Figure 3: Critical regions in vertical slices (a) before Step 6 and (b) after Step 6
In the entire array there are at most 2 dirty rows (Figure 2e).
Step 6
In Step 6 the two last dirty rows are sorted in alternating direction. Possibly still unsorted are the at most n1/4 · n1/2 = n3/4 elements from the critical regions (Figure 3b / Figure 2f). These elements form an unsorted zone of length at most n3/4.
Step 7
In Step 7 the unsorted zone of length at most n3/4 is sorted according to the snake.
Due to the 0-1-principle, the algorithm sorts every arbitrary data, because it sorts all 0-1-sequences.
Analysis
An analysis of the algorithm yields the following:
| Step 1: | sorting the blocks | O(n3/4) | ||
| Step 2: | unshuffle along the rows | n | ||
| Step 3: | sorting the blocks | O(n3/4) | ||
| Step 4: | sorting the columns | n | ||
| Step 5: | sorting the vertical slices | O(n3/4) | ||
| Step 6: | sorting the rows in alternating direction | n | ||
| Step 7: | n3/4 steps of odd-even transposition sort | O(n3/4) | ||
| altogether: | 3n + O(n3/4) |
The blocks can be sorted using any linear sorting algorithm, e.g. 4-way mergesort.
In Step 5, the vertical slices can be sorted in time O(n3/4), because they contain a region of only n1/4 dirty rows (e.g. by sorting the blocks and subsequently sorting the blocks vertically overlapping by n1/4 rows).
Conclusions
The algorithm 3n-sort of Schnorr/Shamir for sorting an n×n-array has a time complexity of 3n + O(n3/4). It is asymptotically optimal as well as regarding the constant, since 3n is a lower bound for sorting on an n×n-array. The algorithm of Schnorr/Shamir is simpler than the algorithm of Thompson/Kung [TK 77] which is also optimal with a time complexity of 3n + O(n2/3·log(n)).
References
[SchSh 86] C.P. Schnorr, A. Shamir: An Optimal Sorting Algorithm for Mesh-Connected Computers. Proc. of the 18th ACM Symposium on Theory of Computing, 255-261 (1986)
[TK 77] C.D. Thompson, H.T. Kung: Sorting on a Mesh-Connected Parallel Computer. Communications of the ACM, 20, 4, 263-271 (1977)
Next: [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 23.05.2001 Updated: 07.02.2023