Sortierverfahren

Mergesort iterativ

Im Sortierverfahren Mergesort werden jeweils zwei sortierte Teilstücke der zu sortierenden Folge zu einem sortierten Teilstück verschmolzen (engl.: to merge – verschmelzen). Wird dieses Konzept top-down umgesetzt, so ergibt sich die rekursive Version von Mergesort. Bei der bottom-up-Umsetzung ergibt sich eine iterative Version. In dieser Version werden erst alle Teilstücke der Folge der Länge 1, dann alle Teilstücke der Länge 2, der Länge 4 usw. zu sortierten Teilstücken verschmolzen, so lange, bis die gesamte Folge sortiert ist [Sed 03].

Eine gewisse Schwierigkeit tritt auf, wenn die Länge n der Folge keine Zweierpotenz ist. Dann muss gelegentlich ein kürzeres und ein längeres Teilstück miteinander verschmolzen werden (Bild 1 b).

Da beim Merge-Verfahren jeweils das erste Teilstück in ein Hilfsarray ausgelagert wird, ist es günstig, wenn das erste Teilstück das kürzere ist. Dies wird erreicht, indem in der Funktion mergesort die Teilstücke der Länge s = 1, 2, 4, 8, ... vom Ende der Folge her abgearbeitet werden. Der Index m, der auf das letzte Element des jeweiligen ersten Teilstücks zeigt, läuft abwärts (vgl. Bild 2).

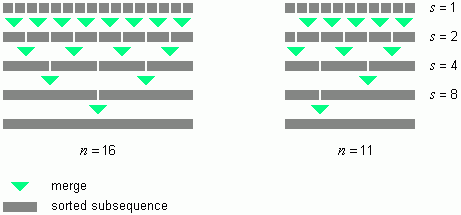
Bild 1: Verschmelzen von sortierten Teilstücken beim iterativen Mergesort-Verfahren

Die folgende Klasse IterativeMergeSorter kapselt die Funktionen mergesort und merge. Die Funktion merge ist dieselbe wie die Variante b im rekursiven Verfahren.

Die Methode sort übergibt das zu sortierende Array an das Array a, legt das Hilfsarray b an und ruft mergesort auf.

Es folgt das Programm. Die Rolle der Variablen s und m in der Funktion mergesort wird in folgendem Bild 2 verdeutlicht.

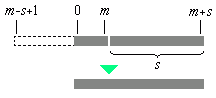
Bild 2: Indexpositionen beim Verschmelzen eines kürzeren und eines längeren Teilstücks

public class IterativeMergeSorter
{
    private int[] a;
    private int[] b;    // Hilfsarray
    private int n;

    public void sort(int[] a)
    {
        this.a=a;
        n=a.length;
        b=new int[n/2];
        mergesort();
    }

    private void mergesort()
    {
        int m, s;
        for (s=1; s<n; s+=s)
            for (m=n-1-s; m>=0; m-=s+s)
                merge(max(m-s+1, 0), m, m+s);
    }

    // Variante b
    void merge(int lo, int m, int hi)
    {
        int i, j, k;

        i=0; j=lo;
        // vordere Hälfte von a in Hilfsarray b kopieren
        while (j<=m)
            b[i++]=a[j++];

        i=0; k=lo;
        // jeweils das nächstgrößte Element zurückkopieren
        while (k<j && j<=hi)
            if (b[i]<=a[j])
                a[k++]=b[i++];
            else
                a[k++]=a[j++];

        // Rest von b falls vorhanden zurückkopieren
        while (k<j)
            a[k++]=b[i++];
    }

    private int max(int a, int b)
    {
        return a>b? a: b;
    }

}    // end class IterativeMergeSorter

[Sed 03] R. Sedgewick: Algorithms in Java, Parts 1-4. 3. Auflage, Addison-Wesley (2003)

[Lan 12] H.W. Lang: Algorithmen in Java. 3. Auflage, Oldenbourg (2012)

Die iterative Version von Mergesort sowie andere Sortierverfahren, etwa Quicksort, Heapsort und Shellsort, finden Sie auch in meinem Buch über Algorithmen.
Weitere (vertikaler Abstand) Themen des Buches: Textsuche, Graphenalgorithmen, algorithmische Geometrie, Arithmetik, Codierung, Kryptografie, parallele Sortieralgorithmen.

[Weitere Informationen]

Weiter mit: [Natural Mergesort] oder [up]

H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 16.04.2005 Updated: 05.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden

Sortierverfahren

Mergesort iterativ

Programm

Literatur