Median-Algorithmus | |
In einer sortierten Datenfolge ist es leicht, das größte Element, das zweitgrößte usw. zu finden. In einer nicht sortierten Folge ist es schwieriger. Man könnte natürlich die Folge zunächst sortieren. Das Sortieren einer Datenfolge der Länge n dauert aber Ω(n log(n)) Schritte. Um das Maximum zu bestimmen, ist es tatsächlich nicht nötig, die Folge zu sortieren. Es genügt ein Durchlauf durch die Folge, dies sind O(n) Schritte.
Wie aber verhält es sich, wenn nicht das Maximum oder Minimum, sondern das k-größte Element gesucht ist? Ist das Problem umso schwieriger, je weiter k sich n/2 nähert? Es stellt sich heraus, dass dies in Bezug auf die Zeitkomplexität nicht der Fall ist. Das k-größte Element lässt sich in Zeit O(n) bestimmen [BFPRT 72].
Problem
Definition: Sei (M,  ) eine Menge mit einer Ordnungsrelation und a = a0, ..., an-1 eine endliche Folge von Elementen ai
) eine Menge mit einer Ordnungsrelation und a = a0, ..., an-1 eine endliche Folge von Elementen ai  M. Ein Element ai der Folge hat den Rang k, wenn es in der sortierten Folge an Position k steht.
M. Ein Element ai der Folge hat den Rang k, wenn es in der sortierten Folge an Position k steht.
Beispiel: Sei n = 7 und a = a0, ..., an-1 = 7 5 9 2 3 6 8. Das Element a3 = 2 hat den Rang 0, a5 = 6 hat den Rang 3. Denn in der sortierten Folge 2 3 5 6 7 8 9 steht die 2 an Position 0 und die 6 an Position 3.
Wenn die Elemente der Folge alle verschieden sind, ist der Rang jedes Elementes eindeutig bestimmt. Das kleinste Element hat den Rang 0, das zweitkleinste den Rang 1, das größte den Rang n-1.
Wenn in der Folge gleiche Elemente vorkommen, so kann ein Element mehrere (aufeinander folgende) Ränge haben. Umgekehrt ist aber für jeden Rang das zugehörige Element eindeutig bestimmt.
Beispiel: Sei n = 7 und a = a0, ..., an-1 = 7 5 2 5 3 6 2. Die sortierte Folge ist 2 2 3 5 5 6 7. Das Element a6 = 2 hat den Rang 0 und den Rang 1. Das Element mit Rang 4 ist die 5.
Um zu einem gegebenem Rang k das zugehörige Folgenelement p zu bestimmen, liegt es nahe, die Folge zu sortieren, dann ist das gesuchte Element p = ak. Diese Vorgehensweise hat allerdings die Komplexität Θ(n log(n)).
Tatsächlich ist es jedoch möglich, das Element mit dem Rang k auch in Zeit Θ(n) zu bestimmen. Von besonderem Interesse ist die Berechnung des Medians, d.h. des mittleren Elements in der sortierten Folge.
Definition: Sei a = a0, ..., an-1 eine endliche Folge. Der Median der Folge ist das Element mit dem Rang (n-1) div 2.
Idee
Ein einfacher Algorithmus nach dem Divide-and-Conquer-Prinzip zur Bestimmung des Elementes mit dem Rang k geht folgendermaßen vor:
zur Bestimmung des Elementes mit dem Rang k geht folgendermaßen vor:
| Prozedur simpleElementOfRank(k) | |
| Eingabe: | Folge a0, ..., an-1 der Länge n   , Zahl k , Zahl k  {0, ..., n-1} {0, ..., n-1}
|
| Ausgabe: | Element der Folge mit Rang k |
| Methode: |
|
Im letzten Schritt ist vorausgesetzt, dass der Rang eines Elements in einem Teilstück sich auf die tatsächliche Indexposition bezieht. Der Rang des kleinsten Elements im Teilstück ar, ..., as ist also r und nicht 0.
Das Partitionieren der Folge kann in linearer Zeit durchgeführt werden (siehe weiter unten). Jedes der drei Teilstücke ist kürzer als die ursprüngliche Folge, daher bricht die Rekursion irgendwann ab. Im schlechtesten Fall geschieht dies allerdings, ähnlich wie bei Quicksort, erst nach n-1 Aufrufen, in denen Teilstücke der Länge n-1, n-2, ..., 1 behandelt werden. Dies ergibt insgesamt eine Komplexität von Θ(n2).
Der beste Fall tritt ein, wenn das erste und das dritte Teilstück gleichlang sind. Dann ergibt sich eine Komplexität von höchstens c·(n + n/2 + n/4 + ... + 1)  O(n).
O(n).
Auch im Durchschnitt ergibt sich eine Komplexität von O(n).
Linearer Median-Algorithmus
Um auch im schlechtesten Fall eine Komplexität von O(n) zu erreichen, muss das Vergleichselement x sorgfältiger ausgewählt werden. Der Wert von x darf nicht zu nahe am größten und nicht zu nahe am kleinsten Element der Folge liegen. Am besten wäre es, als Vergleichselement den Median der Folge zu nehmen. Diesen zu berechnen ist aber sicherlich genauso schwer, wie allgemein das Element mit dem Rang k zu berechnen.
Tatsächlich genügt es, als Vergleichselement einen Wert zu nehmen, der hinreichend nahe am Median liegt. Dieser Wert ist der Median der Mediane von jeweils 5 Elementen.
Um die n/5 Mediane von je 5 Elementen der Folge zu berechnen, ist linearer Aufwand erforderlich. Um den Median m dieser Mediane zu berechnen, ist ein rekursiver Aufruf von elementOfRank, mit deutlich reduzierter Problemgröße n/5, erforderlich.
Es bleibt zu zeigen, dass die Partitionierung der Folge anhand des Vergleichselements m deutlich kürzere Teilstücke als die ursprüngliche Folge liefert.
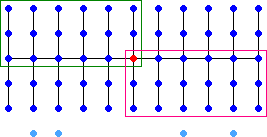
Hierzu stellen wir uns die Elemente der Folge a = a0, ..., an-1 in folgendem Schema angeordnet vor (Bild 1):
| |
| Bild 1: Anordnung der Elemente um den Median der Mediane | |
In der mittleren Zeile stehen die Mediane von jeweils 5 Elementen, sortiert von links nach rechts. Die zugehörigen 5 Elemente stehen in der jeweiligen Spalte, sortiert von oben nach unten. In der Mitte des Feldes steht der Median der Mediane m. Wenn n nicht durch 5 teilbar ist, stehen in einer weiteren Zeile noch bis zu 4 Elemente (hellblau).
In Wirklichkeit wird die Datenfolge nicht in dieser Weise angeordnet. Es ist jedoch möglich, sie so anzuordnen, und daran ist zu erkennen, dass es mindestens n/4 Elemente in der Folge gibt, die kleiner oder gleich m sind (grün eingerahmt) und ebenfalls mindestens n/4 Elemente, die größer oder gleich m sind (rot eingerahmt). Dies bedeutet, dass es höchstens 3/4 n Elemente gibt, die größer als m sind und höchstens 3/4 n Elemente, die kleiner als m sind.
Ab n = 15 gilt diese Tatsache auch für den Fall, dass die Anzahl der Elemente n nicht durch 5 teilbar ist.
In der folgenden Prozedur elementOfRank wird der Median der Mediane von je 5 Elementen als Vergleichselement für die Partitionierung der Datenfolge verwendet. Die Prozedur berechnet das k-größte Element der eingegebenen Folge. Der Median der Folge lässt sich also durch den Aufruf elementOfRank((n-1) div 2) ermitteln.
| Prozedur elementOfRank(k) | |
| Eingabe: | Folge a0, ..., an-1 der Länge n   , Zahl k , Zahl k  {0, ..., n-1} {0, ..., n-1}
|
| Ausgabe: | Element der Folge mit Rang k |
| Methode: |
|
Analyse
Die Komplexität T(n) der Prozedur elementOfRank ergibt sich wie folgt:
| Schritt 1: | O(1) | |
| Schritt 2: | O(n) | |
| Schritt 3: | T(n/5) | |
| Schritt 4: | O(n) | |
| Schritt 5: |  T(3/4 n) T(3/4 n) |
Mit c sei die Konstante bezeichnet, die in der O-Notation von Schritt 2 und Schritt 4 zusammengenommen verborgen ist. Dann ergibt sich eine Gesamtkomplexität von
T(n)  20·c·n
20·c·n  O(n).
O(n).
Implementierung
Median von je 5 Elementen
Um die Mediane von je 5 Elementen zu bestimmen, stellen wir uns die Datenfolge als zweidimensionales Feld mit n div 5 Spalten vor (ähnlich Bild 1). Wenn die Spalten sortiert werden, erscheinen die Mediane in der dritten Zeile des Feldes. In diesem zusammenhängenden Teilstück der Datenfolge wird durch rekursiven Aufruf des Median-Algorithmus der Median der Mediane ermittelt.
Zum Sortieren der (gedachten) Spalten wird Insertionsort verwendet, in einer ähnlichen Implementation wie bei Shellsort.
void sort5(int lo, int n) { int i, j, h, t; h=n/5; for (i=lo+h; i<lo+n; i++) { j=i; t=a[j]; while (j>=lo+h && a[j-h]>t) { a[j]=a[j-h]; j=j-h; } a[j]=t; } } |
Partitionierung
Für Schritt 3 der Prozedur elementOfRank wird folgende Prozedur partition verwendet. Die Prozedur partitioniert anhand eines Vergleichselements x einen Abschnitt der Länge n des Arrays a, beginnend beim Index lo, in die drei erwähnten Teilstücke. Als Ergebnis wird das Zahlenpaar (q, g) zurückgeliefert, das den Beginn des zweiten Teilstücks (Index q) und des dritten Teilstücks (Index g) kennzeichnet.
Pair partition (int lo, int n, int x) { int q=lo, g=lo, i, y; for (i=lo; i<lo+n; i++) { y=a[i]; if (y<=x) { exchange(i, g++); if (y<x) exchange(g-1, q++); } } return new Pair(q, g); } |
Die Funktionsweise der Prozedur partition wird durch Bild 2 bis Bild 5 veranschaulicht, hier für lo = 0.
Zu jedem Zeitpunkt besteht das Feld aus vier Teilstücken: aus den Elementen, die kleiner als das Vergleichselement x sind (Indexpositionen 0, ..., q-1, gelb dargestellt), aus denen, die gleich x sind (q, ..., g-1, grün) und denen, die größer als x sind (g, ..., i-1, blau) sowie aus den noch zu untersuchenden Elementen (i, ..., n-1, weiß). Bild 2 zeigt diese Situation.
| |
| Bild 2: Bereits partitionierter Bereich | |
| |
| Bild 3: Einordnen eines Elements a[i]>x | |
| |
| Bild 4: Einordnen eines Elements a[i]=x | |
| |
| Bild 5: Einordnen eines Elements a[i]<x | |
Ist das nächste zu untersuchende Element a[i] größer als x, so ist nichts zu tun (Bild 3). Ist es gleich x, so wird es durch die in Bild 4 gezeigte Vertauschung in den mittleren Bereich eingeordnet; der Beginn des hinteren Bereichs wird durch g++ angepasst.
Dasselbe geschieht auch, wenn es kleiner als x ist; zusätzlich wird es dann in einer weiteren Vertauschung in den vorderen Bereich eingeordnet. Der Beginn des mittleren Bereichs wird durch q++ entsprechend angepasst (Bild 5).
Zum Schluss wird jeweils mit i++ der bereits partitionierte Bereich um 1 vergrößert.
Literatur
Weiter mit:
 |
|
|
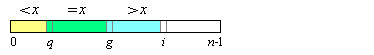
![Bild 3: Einordnen eines Elements a[i]>x](median0.gif)
![Bild 4: Einordnen eines Elements a[i]=x](median1.gif)
![Bild 5: Einordnen eines Elements a[i]<x](median2.gif)
 Themen des Buches: Sortieren, Textsuche, Graphenalgorithmen, Arithmetik, Codierung, Kryptografie, parallele Sortieralgorithmen.
Themen des Buches: Sortieren, Textsuche, Graphenalgorithmen, Arithmetik, Codierung, Kryptografie, parallele Sortieralgorithmen.

