Textsuche
Knuth-Morris-Pratt-Algorithmus
Idee
Der naive Algorithmus hat den Nachteil, dass er bei einem Mismatch alle Zeichen, die bis dahin schon übereingestimmt haben, wieder vergisst und von vorne anfängt zu vergleichen. Auf diese Weise kommt seine Komplexität von Θ(n·m) Vergleichen im schlechtesten Fall zustande (n: Länge des Textes, m: Länge des Musters).
Der Algorithmus von Knuth, Morris und Pratt [KMP 77] nutzt die bei Übereinstimmung von Zeichen gewonnene Information aus. So brauchen die Zeichen nach einem Mismatch nicht noch einmal alle wieder von vorn verglichen zu werden. Im Ergebnis benötigt der Algorithmus in der Suchphase nur noch O(n) Vergleiche.
In einem Vorlauf (preprocessing) analysiert der Algorithmus zunächst das Muster und speichert Information über seine Struktur in einem Array der Länge m. Die Vorlaufphase lässt sich in Zeit O(m) durchführen. Da m≤n, hat der gesamte Algorithmus eine Komplexität von O(n).
Das Verfahren lässt sich auch als Simulation eines speziellen nichtdeterministischen endlichen Automaten, eines String-Matching-Automaten, auffassen.
Grundlagen
Definition: Sei A ein Alphabet und x = x0 ... xk-1, k ∈ ℕ ein Wort der Länge k über A.
Ein Präfix von x ist ein Teilwort u mit
u = x0 ... xb-1 wobei b ∈ {0, ..., k}
also ein Anfangswort der Länge b von x.
Ein Suffix von x ist ein Teilwort u mit
u = xk-b ... xk-1 wobei b ∈ {0, ..., k}
also ein Endwort der Länge b von x.
Ein Präfix u von x bzw. ein Suffix u von x heißt echt, wenn u ≠ x ist, d.h. wenn die Länge b<k ist.
Ein Rand von x ist ein Teilwort r mit
r = x0 ... xb-1 und r = xk-b ... xk-1
wobei b ∈ {0, ..., k-1}
Ein Rand von x ist also ein Wort, das gleichzeitig echtes Präfix und echtes Suffix von x ist.
Die Länge b wird als die Breite des Randes r bezeichnet.
Beispiel: Sei x = abacab. Die echten Präfixe von x sind
ε, a, ab, aba, abac, abaca
Die echten Suffixe von x sind
ε, b, ab, cab, acab, bacab
Ränder von x sind
ε, ab
Der Rand ab hat die Breite 2.
Stets ist das leere Wort ε ein Rand von x, x ∈ A+. Lediglich ε selbst hat keinen Rand.
In folgendem Beispiel wird deutlich, wie mithilfe des Begriffes "Rand" die Schiebedistanz beim Knuth-Morris-Pratt-Algorithmus ermittelt wird.
Beispiel:
Die Zeichen an den Positionen 0, ..., 4 haben übereingestimmt. Der Vergleich c-d an Position 5 ergibt einen Mismatch. Das Muster kann bis Position 3 weitergeschoben werden, und der Vergleich wird ab Position 5 des Textes fortgesetzt.
Die Schiebedistanz richtet sich nach dem breitesten Rand des übereinstimmenden Präfixes des Musters. In diesem Beispiel ist das übereinstimmende Präfix abcab; es hat die Länge j = 5. Sein breitester Rand ist ab mit der Breite b = 2. Die Schiebedistanz beträgt j – b = 5 – 2 = 3.
Die im Vorlauf zu gewinnende Information besteht also darin, für jedes Präfix des Musters die Länge seines breitesten Randes zu bestimmen.
Vorlauf
Satz: Seien r, s Ränder eines Wortes x, wobei |r| < |s|. Dann ist r ein Rand von s.
Beweis: Bild 1 zeigt schematisch das Wort x mit den Rändern r und s. Als Rand von x ist r Präfix von x und damit, weil kürzer als s, auch echtes Präfix von s. Aber r ist auch Suffix von x und damit echtes Suffix von s. Also ist r Rand von s.

Bild 1: Ränder r, s eines Wortes x
Ist s der breiteste Rand von x, so ergibt sich der nächstschmalere Rand r von x als breitester Rand von s usw.
Definition: Sei x ein Wort und a ∈ A ein Zeichen. Ein Rand r von x lässt sich durch a fortsetzen, wenn ra Rand von xa ist.
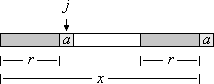
Bild 2: Fortsetzung eines Randes
Anhand von Bild 2 ist zu sehen, dass sich ein Rand r der Breite j von x durch a fortsetzen lässt, wenn xj = a ist.
In der Vorlaufphase wird ein Array b der Länge m+1 berechnet. Der Eintrag b[i] enthält für jedes Präfix der Länge i des Musters die Breite seines breitesten Randes (i = 0, ..., m). Das Präfix ε der Länge i = 0 hat keinen Rand; daher wird b[0] = -1 gesetzt.
![Bild 3: Präfix der Länge i des Musters mit Rand der Breite b[i]](rand4.gif)
Bild 3: Präfix der Länge i des Musters mit Rand der Breite b[i]
Sind die Werte b[0], ..., b[i] bereits bekannt, so ergibt sich der Wert b[i+1], indem geprüft wird, ob sich ein Rand des Präfixes p0 ... pi-1 durch pi fortsetzen lässt. Dies ist der Fall, wenn pb[i] = pi ist (Bild 3). Die zu prüfenden Ränder ergeben sich nach obigem Satz in absteigender Breite aus den Werten b[i], b[b[i]] usw.
Der Vorlaufalgorithmus enthält daher eine Schleife, die diese Werte durchläuft. Ein Rand der Breite j lässt sich durch pi fortsetzen, wenn pj = pi ist. Wenn nicht, wird j = b[j] gesetzt und damit der nächstschmalere Rand geprüft. Die Schleife endet spätestens, wenn sich kein Rand fortsetzen lässt (j = -1).
Nach Erhöhung von j durch die Anweisung j++ enthält j in jedem Fall die Breite des breitesten Randes von p0 ... pi. Dieser Wert wird in b[i+1] eingetragen (in b[i] nach Erhöhung von i durch die Anweisung i++).
Vorlaufalgorithmus
{
int i=0, j=-1;
b[i]=j;
while (i<m)
{
while (j>=0 && p[i]!=p[j]) j=b[j];
i++; j++;
b[i]=j;
}
}
Beispiel: Für das Muster p = ababaa ergeben sich die Randbreiten im Array b wie folgt. Beispielsweise ist b[5] = 3, weil das Präfix ababa der Länge 5 einen Rand der Breite 3 hat.
Suchalgorithmus
Konzeptionell könnte der obige Vorlaufalgorithmus statt auf p auf das Wort pt angewendet werden. Wenn nur Ränder bis zur maximalen Breite m berechnet werden, so entspricht ein Rand der Breite m eines Präfixes x von pt einem Vorkommen des Musters in t, wenn der Rand sich nicht überschneidet (Bild 4).

Bild 4: Rand der Länge m eines Präfixes x von pt
Hierdurch ist die große Ähnlichkeit des folgenden Suchalgorithmus mit dem Vorlaufalgorithmus zu erklären.
Knuth-Morris-Pratt-Suchalgorithmus
{
int i=0, j=0;
while (i<n)
{
while (j>=0 && t[i]!=p[j]) j=b[j];
i++; j++;
if (j==m)
{
report(i-j);
j=b[j];
}
}
}
In der inneren While-Schleife wird bei einem Mismatch an Position j der breiteste Rand des übereinstimmenden Präfixes des Musters betrachtet (Bild 5). Dieser hat die Breite b[j]. Indem an Position b[j] weiterverglichen wird, ergibt sich eine neue Ausrichtung des Musters. Diese berücksichtigt somit das breiteste Präfix des Musters, das bereits übereingestimmt hat. Die While-Schleife wird solange durchlaufen, bis Übereinstimmung vorliegt oder kein Rand mehr vorhanden ist (j = -1).
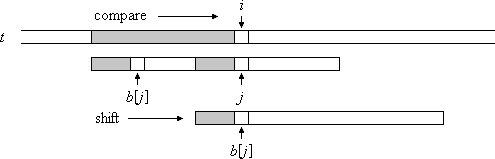
Bild 5: Verschieben des Musters bei einem Mismatch an Position j
Wenn alle m Zeichen des Musters mit dem entsprechenden Textfenster übereingestimmt haben (j = m), wird durch die Funktion report(i-j) die Position des Vorkommens gemeldet. Anschließend wird das Muster so weit verschoben, wie es sein breitester Rand zulässt.
Das folgende Beispiel zeigt die Vergleiche, die der Suchalgorithmus durchführt: Übereinstimmungen (grün) und Mismatches (rot).
Beispiel:
Analyse
Die innere While-Schleife des Vorlaufalgorithmus vermindert bei jedem Durchlauf den Wert von j um mindestens 1, denn es ist stets b[j] < j. Da die Schleife spätestens bei j = -1 abbricht, kann sie den Wert von j höchstens so oft vermindern, wie er vorher durch j++ erhöht wurde. Da j++ in der äußeren Schleife insgesamt genau m-mal ausgeführt wird, kann die Gesamtanzahl aller Durchläufe durch die While-Schleife auch nur maximal m betragen. Der Vorlaufalgorithmus benötigt daher höchstens O(m) Schritte.
Mit derselben Argumentation ist einzusehen, dass der Suchalgorithmus höchstens O(n) Schritte benötigt. Anschaulich wird dies auch anhand des obigen Beispiels klar: die durchgeführten Vergleiche (grüne und rote Zeichen) bilden eine Treppe. Jede Stufe der Treppe kann höchstens so hoch sein, wie sie breit ist, somit werden höchstens 2n Vergleiche durchgeführt.
Da m ≤ n, beträgt die Komplexität des gesamten Verfahrens ebenfalls O(n).
Literatur
[KMP 77] D.E. Knuth, J.H. Morris, V.R. Pratt: Fast Pattern Matching in Strings. SIAM Journal of Computing 6, 2, 323-350 (1977)
[Lan 12] H.W. Lang: Algorithmen in Java. 3. Auflage, Oldenbourg (2012)
Das Verfahren von Knuth-Morris-Pratt und andere Textsuchverfahren, so etwa die Verfahren von Boyer-Moore, Horspool und Sunday finden Sie auch in meinem Buch über Algorithmen.
Weitere Themen des Buches: Sortieren, Graphenalgorithmen, Arithmetik, Codierung, Kryptografie, parallele Sortieralgorithmen.
[Web 1] http://www-igm.univ-mlv.fr/~lecroq/string/
[Web 2] http://hwlang.de/algorithmen/pattern/stringmatchingclasses/KmpStringMatcher.java Knuth-Morris-Pratt-Algorithmus als Java-Programm
[Web 3] http://hwlang.de/algorithmen/pattern/patternmatcher.htm#section4 Knuth-Morris-Pratt-Algorithmus als Simulation eines String-Matching-Automaten
Weiter mit: [Boyer-Moore-Algorithmus] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 19.03.2001 Updated: 05.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden
