Graphenalgorithmen
Spielbäume
Problem
Wir betrachten Zwei-Personen-Spiele wie zum Beispiel Schach, Dame oder TicTacToe. Die beiden Spieler A und B führen abwechselnd Spielzüge aus. Nach jedem Zug befindet sich das Spiel in einer bestimmten Spielstellung. Ziel von Spieler A ist es, eine Spielstellung zu erreichen, in der er das Spiel gewonnen hat. Das Problem besteht darin, den jeweils nächsten Zug zu bestimmen, der ihn dieser Gewinnstellung näher bringt.
Spielbaum
Als Beispiel betrachten wir eine mögliche Spielstellung des Spiels TicTacToe; Spieler A ist am Zug. Diese Spielstellung bildet die Wurzel eines Baumes von Folge-Spielstellungen (Bild 1). Je nach dem, wo Spieler A sein Kreuz macht, ergeben sich zunächst drei verschiedene Folge-Spielstellungen. Indem daraufhin Spieler B seinen Kreis macht, ergeben sich davon ausgehend jeweils zwei weitere Folge-Spielstellungen. In zwei dieser Spielstellungen ist das Spiel bereits zu Ende, weil Spieler B drei Kreise in einer Reihe hat und damit gewonnen hat. Ausgehend von den anderen Spielstellungen ergibt sich, indem Spieler A wieder ein Kreuz macht, jeweils noch eine Folge-Spielstellung; danach ist das Spiel zu Ende.

Bild 1: Spielbaum ausgehend von einer Spielstellung des Spiels TicTacToe
Bewertungsfunktion für Spielstellungen
Wir führen eine Bewertungsfunktion ein, die jeder Spielstellung einen Zahlenwert zuweist, der umso höher ist, je günstiger die Spielstellung für Spieler A ist, und umso niedriger, je günstiger die Spielstellung für Spieler B ist. Dann ist es möglich, durch Analyse des Spielbaums den optimalen Zug für Spieler A zu finden.
Im Allgemeinen ist es schwierig, Spielstellungen sinnvoll zu bewerten, beispielsweise eine Spielstellung im Schachspiel. Eine sehr grobe Bewertung würde die Anzahl und Qualität der eigenen Spielfiguren minus die der gegnerischen Spielfiguren heranziehen.
Einfach ist eine Spielstellung dagegen dann zu bewerten, wenn sie eine Gewinnstellung darstellt, in der ein Spieler das Spiel gewonnen hat. Wenn Spieler A gewonnen hat, dann wird diese Spielstellung mit einem sehr großen Wert bewertet und wenn Spieler B gewonnen hat, mit einem sehr kleinen Wert.
Die Bewertungsfunktion wird immer auf die Blätter des Spielbaums angewendet, der gerade betrachtet wird. In Bild 1 ist dies geschehen: Die Spielstellungen, in denen Spieler A gewonnen hat, sind mit 1 bewertet, die Spielstellungen, in denen Spieler B gewonnen hat, mit -1 und die Unentschieden-Spielstellungen mit 0.
Auswertung des Spielbaums: Minimax-Strategie
Aus den Bewertungen der Blätter des Spielbaums werden die Bewertungen der inneren Knoten abgeleitet. Die Vorgehensweise veranschaulicht Bild 2.
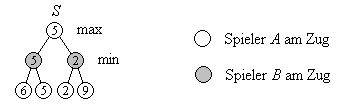
Bild 2: Spielbaum mit Bewertung der Spielstellungen nach zwei Zügen
Ausgehend von Spielstellung S zieht erst Spieler A und dann Spieler B. Nach diesen zwei Zügen ergeben sich an den Blättern des Spielbaums vier mögliche Spielstellungen, die mit 6, 5, 2 bzw. 9 bewertet seien.
Die Bewertungen der inneren Knoten des Spielbaums werden bottom-up berechnet: in Spielstellungen, in denen Spieler B am Zug ist, als das Minimum der Bewertungen der Nachfolgerknoten und in Spielstellungen, in denen Spieler A am Zug ist, als deren Maximum.
Dieser Vorgang wird als Auswertung des Spielbaums nach der Minimax-Strategie bezeichnet.
Die Begründung für diese Art der Berechnung ist folgende: Zieht A ausgehend von Spielstellung S nach rechts, um die mit 9 bewertete Spielstellung zu erreichen, so wird B dies vereiteln, indem er nach links zieht, um die für ihn bessere und für A schlechtere, mit 2 bewertete Spielstellung zu erreichen. Die Strategie von B ist also, stets die minimal bewertete Spielstellung anzusteuern. Hieraus ergibt sich die Bewertung der Knoten, in denen B am Zug ist, als jeweils das Minimum der Bewertungen der Nachfolgerknoten.
Spieler A dagegen versucht stets, die maximal bewertete Spielstellung anzusteuern. Hieraus ergibt sich die Bewertung der Knoten, in denen A am Zug ist, als jeweils das Maximum der Bewertungen der Nachfolgerknoten.
In Bild 2 zieht A ausgehend von Spielstellung S somit nach links, denn so kann er mindestens, egal wie B dann zieht, den Wert 5 erreichen.
Auch in Bild 1 zieht Spieler A nach links, macht also sein Kreuz oben links in die Ecke. Denn die drei Folge-Spielstellungen sind nach Auswertung des Spielbaums mit 0, -1, -1 bewertet.
Bild 3 zeigt einen Spielbaum für vier Züge. Die 16 erreichbaren Spielstellungen sind mit ihren Bewertungen markiert. Die Auswertung des Spielbaums zeigt, dass A eine Spielstellung mit mindestens dem Wert 5 erreichen kann. Dieser Wert ergibt sich, indem bottom-up jeder Knoten mit dem Minimum (wenn Spieler B am Zug ist) bzw. mit dem Maximum (wenn Spieler A am Zug ist) der Werte seiner direkten Nachfolgerknoten markiert wird.
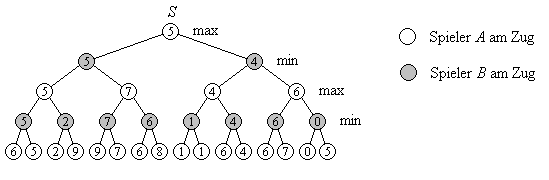
Bild 3: Bewertung der Spielstellungen nach vier Zügen (Blätter des Baumes) und Auswertung des Spielbaums (innere Knoten)
Rekursive Auswertung des Spielbaums
Die Auswertung des Spielbaums vereinfacht sich, wenn die Bewertung der Spielstellungen stets aus Sicht desjenigen Spielers vorgenommen wird, der gerade am Zug ist. Dieser Spieler berechnet stets das Maximum der aus seiner Sicht bewerteten Folgestellungen. Diese Werte sind aber gerade die mit -1 multiplizierten Werte, die sich aus Sicht des Gegners für diese Spielstellungen ergeben.
Statt also abwechselnd das Minimum und das Maximum zu bilden, wird stets das Maximum der mit -1 multiplizierten Werte gebildet; dies führt zum selben Ergebnis. Die Auswertung eval(S) des an einer Spielstellung S beginnenden Spielbaums lässt sich rekursiv wie folgt darstellen:
| eval(S) = |  |
|
Die Funktion rate(S) bewertet hierbei die Spielstellung S aus Sicht des Spielers, der am Zug ist.
Implementierung
Die folgende rekursive Funktion eval wertet einen Spielbaum beginnend an einer Spielstellung s bis zur Tiefe d in Form einer Tiefensuche aus.
Ist d = 0, d.h. besteht der Spielbaum nur aus einem Blatt, so wird als Ergebnis die Bewertung rate(s) der entsprechenden Spielstellung s zurückgegeben (bewertet aus Sicht des Spielers, der am Zug ist).
Ansonsten werden mit dem Iterator s.nextMoveIterator() alle in der Spielstellung s möglichen Spielzüge durchlaufen und die sich daraus ergebenden Folge-Spielstellungen t erzeugt. Durch rekursiven Aufruf der Funktion eval werden die an diesen Spielstellungen t beginnenden Spielbäume der Tiefe d-1 ausgewertet. Von den mit -1 multiplizierten Ergebnissen wird das Maximum gebildet; hierzu wird ein Maximizer verwendet.
{
if (d==0 || s.gameOver())
return rate(s);
Iterator<Move> it=s.nextMoveIterator();
Maximizer<Move> max=new Maximizer<Move>();
Move move;
Configuration t;
while (it.hasNext())
{
move=it.next();
t=s.applyMove(move);
max.add(-eval(t, d-1));
}
return max.getMaxVal();
}
Bestimmen des Spielzugs
Um den optimalen Spielzug zu bestimmen, wird der erste Rekursionsschritt ausgelagert in folgende Funktion findMove, die sich zusätzlich denjenigen Zug move merkt, der den Maximalwert liefert.
{
Iterator<Move> it=s.nextMoveIterator();
Maximizer:(Move> max=new Maximizer<Move>();
Move move;
Configuration t;
while (it.hasNext())
{
move=it.next();
t=s.applyMove(move);
max.add(-eval(t, d-1), move);
}
return max.getMaxObj();
}
Partielle Auswertung des Spielbaums
Tatsächlich brauchen in vielen Fällen nicht alle Knoten des Spielbaums berechnet zu werden. Bild 4 zeigt dies zunächst anhand des Spielbaums von Bild 2.
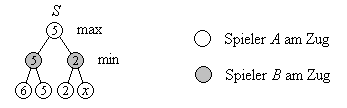
Bild 4: Partielle Auswertung des Spielbaums für zwei Züge
Egal welchen Wert x der untere rechte Knoten hat, er ändert nichts am Ergebnis 5 der Auswertung des Spielbaums. Der Wert des Knotens kann das darüber befindliche Minimum höchstens kleiner machen. Das wiederum darüber befindliche Maximum ist aber bereits größer, bleibt also erhalten.
Bild 5 zeigt anhand des Spielbaums von Bild 3, dass ganze Teilbäume nicht berechnet zu werden brauchen, weil sie zum Ergebnis nicht beitragen. Beispielsweise kann der Wert 4 unterhalb der Wurzel des Spielbaums höchstens kleiner werden, wenn der untere rechte Teilbaum ausgewertet wird. Dadurch ändert sich jedoch am Maximum 5 an der Wurzel nichts. Die Auswertung des Teilbaums ist also nicht nötig.
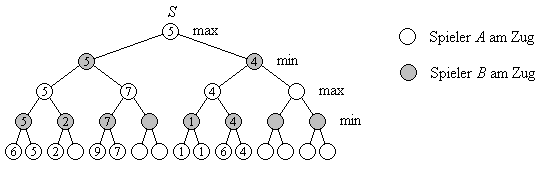
Bild 5: Partielle Auswertung des Spielbaums für vier Züge
Implementierung
Die entsprechende Implementierung entsteht durch eine sehr kleine Abänderung der ursprünglichen Funktion eval.
{
if (d==0 || s.gameOver())
return rate(s);
Iterator<Move> it=s.nextMoveIterator();
Maximizer<Move> max=new Maximizer<Move>();
Move m;
Configuration t;
while (it.hasNext() && max.getMaxVal()<w)
{
m=it.next();
t=s.applyMove(m);
max.add(-eval(t, d-1, -max.getMaxVal()), m);
}
return max.getMaxVal();
}
Beim ersten Aufruf der abgeänderten Funktion eval in der Funktion findMove wird für den Parameter w der Wert Double.POSITIVE_INFINITY eingesetzt.
In der Darstellung von Bild 5 sieht es so aus, als ob die Einsparung an auszuwertenden Spielstellungen nicht allzu groß ist. Dies täuscht allerdings, denn in Wirklichkeit verzweigt ein Spielbaum sehr viel breiter, weil es normalerweise mehr als zwei Zugmöglichkeiten gibt. Entsprechend viele Teilbäume brauchen gegebenenfalls nicht ausgewertet zu werden. Und je tiefer der Spielbaum berechnet wird, umso mehr Knoten fallen weg, wenn ein Teilbaum nicht ausgewertet wird. Je nach tatsächlichem Spiel ergibt sich in der Praxis eine Beschleunigung der Berechnung um Faktoren zwischen 10 und 50.
Literatur
[HS 81] E. Horowitz, S. Sahni: Algorithmen. Springer (1981)
Weiter mit: [Literatur] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 25.10.2006 Updated: 20.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden