Transformationen
Diskrete Cosinus-Transformation (DCT)
Problem
Jeder weiß, dass die Überlagerung von Tönen wieder einen Ton ergibt. Aber ist es umgekehrt möglich, einen beliebigen Ton wieder in seine Grundschwingungen zu zerlegen? Die Antwort ist ja.
In der Praxis liegt der Ton als ein Sample, d.h. als eine Folge von Messwerten an dicht aufeinander folgenden Stellen in einem bestimmten Bereich vor (Bild 1). Gesucht sind einfache, sinusförmige Schwingungen, deren Überlagerung mit dem Ton (zumindest an den Messwerten) übereinstimmt.
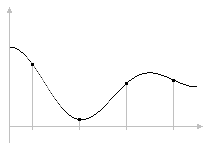
Bild 1: Sample-Werte einer Schwingung
Mathematisch gesehen besteht ein Sample aus den Funktionswerten einer Funktion an bestimmten, vorgegebenen Stützstellen. Die Darstellung der Funktion durch ein Sample heißt Stützstellendarstellung. Gesucht ist die Darstellung der Funktion als gewichtete Summe von bestimmten, vorgegebenen Basisfunktionen. Die Gewichte, mit der die Basisfunktionen in die Summe eingehen, heißen Koeffizienten. Die entsprechende Darstellung der Funktion heißt Koeffizientendarstellung.
Die Umwandlung der Funktion von der Stützstellendarstellung in die Koeffizientendarstellung ist eine Transformation.
Statt eines Tons lassen sich auch beliebige andere Schwingungen auf diese Weise transformieren, und nicht nur Schwingungen, sondern beliebige Samples, z.B. die Grauwerte von nebeneinander liegenden Bildpunkten.
Transformationen spielen bei der Filterung und Kompression von Ton- und Bildsignalen eine bedeutende Rolle. Durch Transformation, Veränderung der Koeffizienten und anschließende Rücktransformation lässt sich das Signal gezielt filtern. Ferner lässt sich durch Verringern der Darstellungsgenauigkeit bei den Koeffizienten die Datenmenge reduzieren. Es zeigt sich, dass die hieraus resultierende Qualitätseinbuße weniger stark wahrnehmbar ist, als wenn die Darstellungsgenauigkeit direkt bei den Sample-Werten verringert würde.
Transformation
Wir definieren zunächst noch einmal genau die Begriffe Stützstellendarstellung und Koeffizientendarstellung.
Definition: Gegeben seien n verschiedene Stützstellen x0, ..., xn-1. Sei ferner f(x) eine Funktion und seien yj = f(xj) die Funktionswerte der Funktion an diesen Stützstellen (j = 0, ..., n-1).
Dann wird der Vektor [y0, ..., yn-1] als Stützstellendarstellung der Funktion f(x) bezeichnet.
Definition: Gegeben seien n Basisfunktionen c0(x), ..., cn-1(x). Sei ferner f(x) eine Funktion, die sich als gewichtete Summe dieser Basisfunktionen ausdrücken lässt:
f(x) = a0·c0(x) + ... + an-1·cn-1(x).
Dann wird der Vektor [a0, ..., an-1] als Koeffizientendarstellung der Funktion f(x) bezeichnet.
Wir betrachten nun zunächst das Problem, aus der Koeffizientendarstellung einer Funktion f(x) die Stützstellendarstellung von f(x) zu berechnen.
Die Funktion f(x) sei in Koeffizientendarstellung gegeben, d.h. als gewichtete Summe von n vorgegebenen Basisfunktionen ci(x):
f(x) = a0·c0(x) + ... + an-1·cn-1(x).
Der Funktionswert yj an einer einzelnen Stützstelle xj ergibt sich durch Einsetzen:
yj = a0·c0(xj) + ... + an-1·cn-1(xj).
In Vektorschreibweise ist dies
| yj = | [a0, ..., an-1] · |
|
Entsprechend lässt sich der Vektor der Funktionswerte an den n Stützstellen x0, ..., xn-1 durch ein Produkt mit einer Matrix, der Transformationsmatrix T, darstellen:
| [y0 ... yn-1] = | [a0 ... an-1] · |
|
Somit lässt sich also die Stützstellendarstellung der Funktion f(x) aus der Koeffizientendarstellung durch Multiplikation mit der Transformationsmatrix T gewinnen:
[y0 ... yn-1] = [a0 ... an-1] · T.
Die Transformationsmatrix T hängt nur von der Wahl der Basisfunktionen ci(x) und der Stützstellen xj ab. Werden die Stützstellen und die Basisfunktionen geeignet gewählt, so lässt sich die Matrix T invertieren.
Dann lässt sich umgekehrt die Koeffizientendarstellung aus der Stützstellendarstellung durch Multiplikation mit der inversen Transformationsmatrix T -1 gewinnen:
[y0 ... yn-1] · T -1 = [a0 ... an-1]
Bei einer invertierbaren Transformationsmatrix T lässt sich also nach Belieben zwischen Koeffizientendarstellung und Stützstellendarstellung hin- und zurücktransformieren.
Diskrete Cosinustransformation
Bei der Diskreten Cosinustransformation werden als Basisfunktionen die Cosinusfunktionen ci(x) = cos(i·x) und als Stützstellen die Werte xj = (j+1/2)·π/n verwendet (Bild 2).
In folgendem Bild 2 sind für den Fall n = 4 die Basisfunktionen cos(i·x) und die Stützstellen (j+1/2)·π/n dargestellt (i, j ∈ {0, ..., 3}).
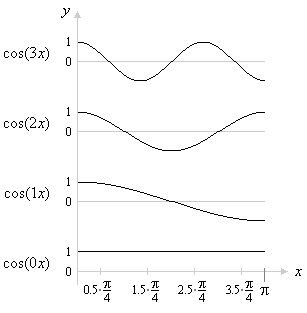
Bild 2: Basisfunktionen cos(i·x) sowie Stützstellen (j+1/2)·π/n
Aus praktischen Gründen werden die Cosinusfunktionen ci noch mit konstanten Faktoren si skaliert, und zwar ist
s0 = 1/
n und
si = 2/n für i > 0.
Entsprechend ergibt sich die Transformationsmatrix T als
Ti,j = si · ci(xj) = si · cos(i·(j+1/2)·π/n)
für alle i, j ∈ {0, ..., n-1}.
Die Skalierung hat zur Folge, dass für die Transformationsmatrix T gilt
T -1 = T T
d.h. die Inverse von T ergibt sich einfach durch Transponieren von T.
Für n = 4 ist die Transformationsmatrix somit
| T = |  |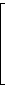
|  |
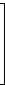Die Diskrete Cosinustransformation ist definiert als Umwandlung von der Stützstellendarstellung in die Koeffizientendarstellung. Entsprechend ist der zu transformierende Vektor [y0 ... yn-1] mit T -1 = T T zu multiplizieren:
[y0 ... yn-1] · T T = [a0 ... an-1]
Die Auswertung dieser Vektor-Matrix-Multiplikation liefert für n = 8 die in der Literatur häufig genannte Formel für die Diskrete Cosinustransformation. Wenn n festliegt, werden die Werte Ti,j der Transformationsmatrix allerdings zweckmäßigerweise im voraus berechnet und gespeichert, daher wird diese Formel in dieser Form dann nicht benötigt:
aj = 
i = 0, ..., 7 yi · Tj,i
= i = 0, ..., 7 yi · sj · cos(j·(i+1/2)·π/8)
= sj · i = 0, ..., 7 yi · cos(j·(2i+1)·π/16)
mit s0 = 1/8 = 2/4 und sj = 2/8 = 1/2 für j > 0.
Zweidimensionale Diskrete Cosinustransformation
Bei Bilddaten ist statt eines Vektors [y0 ... yn-1] eine n × n-Matrix Y von Grauwerten zu transformieren. Diese zweidimensionale Transformation lässt sich auf die eindimensionale Transformation zurückführen.
Zunächst werden alle Zeilenvektoren der Matrix Y eindimensional transformiert, d.h. mit der inversen Transformationsmatrix T T multipliziert.
Dies entspricht einer Matrixmultiplikation
Y · T T = A.
Das Ergebnis A ist eine n × n-Matrix, deren Zeilenvektoren die Ergebnisvektoren der eindimensionalen Transformationen sind.
Nun werden die Spaltenvektoren der Matrix A eindimensional transformiert. Realisiert wird dies, indem A transponiert und mit T T multipliziert wird. Das Ergebnis wird erneut transponiert.
Dies entspricht der Matrixmultiplikation
(AT · T T)T = T · A.
Insgesamt wird also gerechnet
B = T · Y · T T
d.h. es werden zwei Matrixmultiplikationen ausgeführt. Die Matrix B ist das Ergebnis der zweidimensionalen Diskreten Cosinustransformation der Matrix Y.
Zusammenfassung
Bei der eindimensionalen Diskreten Cosinustransformation werden die n zu transformierenden Werte als Stützstellendarstellung einer Funktion aufgefasst, wobei n Stützstellen zwischen 0 und π zugrunde gelegt werden. Die Funktion wird nun von der Stützstellendarstellung in die Koeffizientendarstellung umgewandelt, d.h. die Funktion wird als gewichtete Summe von Basisfunktionen dargestellt. Die Basisfunktionen sind die Cosinusfunktionen cos(i·x). Die Transformation entspricht einer Vektor-Matrix-Multiplikation.
Die zweidimensionale Diskrete Cosinustransformation lässt sich auf den eindimensionalen Fall zurückführen. Die Transformation entspricht zwei Matrix-Multiplikationen.
Literatur
[MH 04] B. Meffert, O. Hochmuth: Werkzeuge der Signalverarbeitung. Pearson Studium (2004)
[Lan 12] H.W. Lang: Algorithmen in Java. 3. Auflage, Oldenbourg (2012)
Die diskrete Cosinus-Transformation (DCT) finden Sie auch in meinem Buch über Algorithmen.
Weitere
Themen des Buches: Sortieren, Textsuche, Graphenalgorithmen, Arithmetik, Codierung, Kryptografie, parallele Sortieralgorithmen.
Weiter mit: [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 27.02.2005 Updated: 08.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden