Codierungstheorie
Lineare Codes
Grundlagen
Definition: Ein Blockcode C ⊆ 𝔹n heißt linearer Code, wenn die Summe zweier Codewörter wieder ein Codewort ist, d.h. wenn gilt
∀ x, y ∈ C : x ⊕ y ∈ C
C bildet damit einen Vektorraum, und zwar einen Teilraum des Vektorraums 𝔹n.
Beispiel: Der 3-Bit-Binärcode mit Paritätsbit C4,3 ist ein linearer Code:
| 0 0 0 0 |
| 0 0 1 1 |
| 0 1 0 1 |
| 0 1 1 0 |
| 1 0 0 1 |
| 1 0 1 0 |
| 1 1 0 0 |
| 1 1 1 1 |
Die Menge T = {1 0 0 1, 0 1 0 1, 0 0 1 1} ist eine Basis von C4,3. Somit hat C4,3 die Dimension 3.
Satz: Sei C ⊆ 𝔹n ein linearer Code. Dann ist der Hamming-Abstand von C gleich dem minimalen Hamming-Gewicht aller von 0 verschiedenen Codewörter:
d(C) = min{ w(x) | x ∈ C, x ≠ 0 }
Der obige lineare Code C4,3 hat den Hamming-Abstand 2, da alle von 0 verschiedenen Codewörter mindestens das Hamming-Gewicht 2 haben, d.h. mindestens 2 Einsen enthalten.
Definition: Sei C ⊆ 𝔹n ein linearer Code der Dimension k und sei {b1, ..., bk} eine Basis von C.
Die mit den Basisvektoren als Zeilen gebildete k × n-Matrix
| G = | 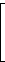 |
| 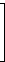 |
heißt Generatormatrix von C.
Die Generatormatrix G erzeugt den Code C, indem alle Produkte von Vektoren aus 𝔹k und G gebildet werden:
C = { a·G | a ∈ 𝔹k }
Anders ausgedrückt ist C der Zeilenraum der Matrix G.
Satz: Durch elementare Zeilenumformungen und Spaltenvertauschungen kann G in die systematische Form
G' = Z·G·S = [ Ik P ]
gebracht werden. Hierbei ist Ik die k × k-Einheitsmatrix und P eine k × (n-k)-Matrix. Die Zeilenumformungen und Spaltenvertauschungen werden repräsentiert durch die Matrizen Z und S. Die Generatormatrix G' erzeugt einen zu C äquivalenten, systematischen Code.
Beispiel: Die oben genannten Basisvektoren von C4,3 untereinander geschrieben ergeben die 3 × 4-Generatormatrix G von C4,3; diese ist bereits in der systematischen Form [I3 P]:
| G' = G = | 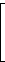 |
| 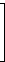 |
Satz: Sei C ⊆ 𝔹n ein linearer Code der Dimension k. Dann ist C ein (n, k)-Code.
Fehlererkennung
Ein linearer Code C ⊆ 𝔹n ist ein Teilraum von 𝔹n. Die Fehlererkennung wird mit Hilfe des zugehörigen Orthogonalraums C⊥ durchgeführt.
Ein Vektor x ∈ 𝔹n gehört zu C genau dann, wenn er zu allen Vektoren von C⊥ orthogonal ist. Dies ist bereits dann der Fall, wenn x zu allen Basisvektoren von C⊥ orthogonal ist. Aus den Basisvektoren von C⊥ lässt sich eine Generatormatrix H von C⊥ bilden. Ist nun x·HT = 0, so ist das Skalarprodukt von x mit allen Basisvektoren von C⊥ gleich 0 und damit x zu allen Basisvektoren von C⊥ orthogonal.
Definition: Sei C ⊆ 𝔹n ein linearer Code und C⊥ der Orthogonalraum von C in 𝔹n. Eine Generatormatrix H von C⊥ heißt Kontrollmatrix von C.
Satz: Sei C ⊆ 𝔹n ein linearer Code mit Kontrollmatrix H. Dann gilt für alle x ∈ 𝔹n
x ∈ C ⇔ x·HT = 0
Das Produkt x·HT wird als das Syndrom von x bezeichnet. Ist das Syndrom ungleich 0, so ist ein Fehler aufgetreten.
Konstruktion einer Kontrollmatrix
Eine Kontrollmatrix H lässt sich aus der Generatormatrix G des linearen Codes konstruieren.
Sei C ⊆ 𝔹n ein linearer Code mit Generatormatrix G. Zunächst wird G in die systematische Form
G' = Z · G · S = [Ik P]
gebracht. Die Matrix G' ist Generatormatrix eines zu C äquivalenten Codes C'.
Nun ist
H' = [PT In-k]
Kontrollmatrix von C'. Durch Rückgängigmachen der durch die Permutationsmatrix S repräsentierten Spaltenvertauschungen ergibt sich eine Kontrollmatrix für den unsprünglichen Code C:
H = H' · ST
Beispiel: Die Generatormatrix G des Codes C4,3 ist G = [I3 P] mit PT = [1 1 1]. Damit ergibt sich die Kontrollmatrix H = [PT I1] = [1 1 1 1]. Für x ∈ 𝔹n liefert x·HT damit die Parität von x. Ist diese gleich 0, so ist x ∈ C, ansonsten ist x ∉ C.
Beim Hamming-Code lässt sich anhand des Syndroms sogar bestimmen, wo der Fehler aufgetreten ist, somit ist hier auch eine Fehlerkorrektur möglich.
Weiter: [Hamming-Code] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 05.03.1997 Updated: 08.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden
