Theoretische Informatik

Definition:  Zwei Grammatiken G und G' werden als äquivalent bezeichnet, wenn sie dieselbe Sprache erzeugen, d.h. wenn gilt

L(G)  =  L(G')

Beispiel:  Die Grammatik G₀ mit den Produktionen

S

aSb  |  ε

und die Grammatik G₁ mit den Produktionen

S		C
C		D
E		ab
D		S  |  aSb  |  aF  |  ε

sind äquivalent, denn beide erzeugen die Sprache { aⁿbⁿ  |  n ∈ ℕ₀ }, wenn auch letztere auf etwas umständliche Weise.

Definition:  Sei G = (V, T, P, S) eine kontextfreie Grammatik und sei A = V ∪ T. Eine Variable X ∈ V heißt

• erreichbar, wenn S 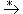   uXv mit u, v ∈ A* gilt,
• produktiv, wenn X 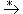   w mit w ∈ T* gilt,
• nutzlos, wenn X nicht erreichbar oder nicht produktiv ist.

Satz:  Zu jeder kontext­freien Grammatik G = (V, T, P, S) gibt es eine äquivalente kontextfreie Grammatik G' = (V', T, P', S) ohne nutzlose Variablen.

Beweis:  Sei w ein Wort mit w ∈ L(G). Dann gibt es eine Ableitungs­folge S 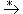 w. Jede Variable, die in den Ableitungs­schritten auf­tritt, ist erreichbar und produktiv. In keiner Ableitungs­folge kann eine nutzlose Variable vorkommen.

G' geht aus G hervor, indem aus V alle nutzlosen Variablen entfernt werden und aus P alle Produktionen, in denen nutzlose Variablen vorkommen.

Beispiel:  In der Grammatik G₁ ist die Variable E nicht erreichbar und die Variable F nicht produktiv, beide Variablen sind also nutzlos. Diese Variablen und die zugehörigen Produktionen werden daher entfernt. Es verbleibt die Grammatik G₂:

S		C
C		D
D		S  |  aSb  |  ε

Definition:  Sei G = (V, T, P, S) eine Grammatik und sei A = V ∪ T. Eine Variable X ∈ V heißt rekursiv, wenn

X 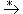   uXv

mit u, v ∈ A* gilt.

Beispiel:  In der Grammatik G₃ des obigen Beispiels ist das Startsymbol S rekursiv.

Satz:  Zu jeder Grammatik G = (V, T, P, S) gibt es eine äquivalente Grammatik G' = (V', T, P', S'), deren Startsymbol S' nicht rekursiv ist.

Beweis:  Die Grammatik G' geht aus der Grammatik G hervor, indem ein neues Startsymbol S' zur Menge der Variablen V hinzugefügt wird und die neue Produktion S'S zur Menge der Produktionen P hinzugefügt wird.

Beispiel:  Indem die angegebene Vorgehens­weise auf die Grammatik G₂ angewendet wird, ergibt sich folgende Grammatik G₃, deren Startsymbol S' nicht rekursiv ist:

S'		S
S		C
C		D
D		S  |  aSb  |  ε

Definition:  Sei G = (V, T, P, S) eine kontextfreie Grammatik. Eine Produktion der Form

X

ε

mit X ∈ V wird als Epsilon-Produktion bezeichnet.

Satz:  Zu jeder kontext­freien Grammatik G = (V, T, P, S) gibt es eine äquivalente kontextfreie Grammatik G' = (V, T, P', S')

• ohne Epsilon-Produktionen, falls ε ∉ L(G)
• mit S'ε als einziger Epsilon-Produktion, falls ε ∈ L(G)

Beweis:  Die kontextfreie Grammatik G wird durch folgendes Verfahren in die Grammatik G' umgeformt.

1. führe die Produktion S'S ein, damit das Startsymbol nicht rekursiv ist
2. bestimme alle Variablen X, aus denen sich das leere Wort ε ableiten lässt:

   V_ε  =  { X ∈ V  |  X 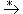 ε }

3. entferne alle Epsilon-Produktionen aus der Grammatik
4. wiederhole solange YuXv mit X ∈ V_ε und |uv| ≥ 1 eine Produktion ist, aber Yuv noch keine Produktion ist

   führe die Produktion Yuv zusätzlich ein

5. wenn S' ∈ V_ε dann

   führe die Produktion S'ε ein

Beispiel:  In der Grammatik G₃ hatten wir Schritt 1 des Verfahrens bereits durchgeführt. In Schritt 2 bestimmen wir nun V_ε  =  { S', S, C, D }. In Schritt 3 entfernen wir die Produktion Dε. In Schritt 4 finden wir DaSb als einzige Produktion mit der dort angegebenen Eigenschaft und führen daher die Produktion Dab neu ein. Und in Schritt 5 schließlich führen wir noch die Produktion S'ε ein, da S' ∈ V_ε.

Das Ergebnis ist die Grammatik G₄:

S'		S  |  ε
S		C
C		D
D		S  |  aSb  |  ab

Definition:  Sei G = (V, T, P, S) eine kontextfreie Grammatik. Eine Produktion der Form

X

Y

mit X, Y ∈ V wird als Ketten­produktion bezeichnet.

Satz:  Zu jeder kontext­freien Grammatik G = (V, T, P, S) gibt es eine äquivalente kontextfreie Grammatik G' = (V', T, P', S) ohne Ketten­produktionen.

Beweis:  Ein Sonderfall von Ketten­produktionen sind Zyklen von Ketten­produktionen. Diese Zyklen werden zuerst entfernt.

Zyklen von Ketten­produktionen entfernen

Wenn die Grammatik einen Zyklus der Form

X₀ → X₁,  X₁ → X₂,   ... ,  X_k-1 → X₀,   k ∈ ℕ

enthält, so lassen sich die Variablen X_i alle ineinander überführen und brauchen daher nicht unter­schieden zu werden. Es werden daher die Produktionen des Zyklus entfernt und alle weiteren Vorkommen der X_i in G durch einen einzigen Repräsentanten ersetzt (falls das Startsymbol S im Zyklus vorkommt, durch S).

Ketten­produktionen entfernen

Jede Ketten­produktion XY wird in der Weise umgeformt, dass für Y die aus Y direkt ableitbaren rechten Seiten eingesetzt werden, so lange, bis keine Ketten­produktionen mehr vorhanden sind.

Beispiel:  

In der Grammatik G₄ ist SC, CD, DS ein Zyklus von Ketten­produktionen. Wir entfernen die Produktionen des Zyklus und ersetzen alle weiteren Vorkommen von S und D durch C. Das Ergebnis ist die Grammatik G₅:

S'		C  |  ε
C		aCb  |  ab

Die Ketten­produktion S'C entfernen wir, indem für deren rechte Seite C die aus C direkt ableitbaren Wörter einsetzen. Es ergibt sich die Grammatik G₆:

S'		aCb  |  ab  |  ε
C		aCb  |  ab

Definition:  Sei G = (V, T, P, S) eine kontextfreie Grammatik. Wir bezeichnen die Grammatik als basis-normalisiert, wenn sie keine keine nutzlosen Variablen, kein rekursives Startsymbol, keine Epsilon-Produktionen außer Sε und keine Ketten­produktionen enthält.

Beispiel:  Die obige Grammatik G₆ ist basis-normalisiert.