Theoretische Informatik
CYK-Algorithmus
Der CYK-Algorithmus (benannt nach den Autoren Cocke, Younger und Kasami) löst das Wortproblem für kontextfreie Sprachen. Es wird kein Stackautomat verwendet. Die Zeitkomplexität des Algorithmus liegt in O(n3). Die kontextfreie Grammatik muss in Chomsky-Normalform vorliegen.
Idee
Gegeben sei eine Grammatik G = (V, T, P, S) in Chomsky-Normalform und ein Wort w = w0 ... wn-1 ∈ T *. Das Wort lässt sich in folgenden zwei Fällen aus einer Variablen Z ableiten:
- es besteht aus einem einzigen Terminalzeichen w0 und die Produktion Z → w0 existiert oder
- es besteht aus zwei Teilwörtern w0, ..., wk-1 und wk, ..., wn-1 , die sich aus den Variablen X bzw. Y ableiten lassen und die Produktion Z → XY existiert (Bild 1).
Um zu entscheiden, ob die zweite Bedingung erfüllt ist, werden alle möglichen Trennstellen k ∈ {1, ..., n-1} zwischen den beiden Teilwörtern betrachtet und die Teilwörter nach denselben beiden Kriterien untersucht.
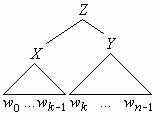
Bild 1: Ableitungsbaum für Wort w
Zunächst liegt es nahe, einen rekursiven Algorithmus zur Implementation dieser Idee in Betracht zu ziehen. Es stellt sich jedoch heraus, dass ein rekursiver Algorithmus viele Berechnungen unnötig mehrfach durchführt. Die Berechnung, aus welchen Variablen sich ein Teilwort wi, ..., wj-1 ableiten lässt, wird für jedes längere Teilwort, dessen Bestandteil es ist, erneut ausgeführt.
Effizienter ist es, diese Berechnung nur einmal auszuführen und das Ergebnis zu speichern, sodass es bei Bedarf wiederverwendet werden kann. Dieser Gedanke führt zu einem Algorithmus nach der Methode der "dynamischen Programmierung".
Algorithmus
Bei der Methode der dynamischen Programmierung werden zunächst die Berechnungen für alle Teilwörter der Länge 1 durchgeführt, dann für alle Teilwörter der Länge 2, 3, usw. Die Ergebnisse werden in einer Tabelle gespeichert und bei jedem weiteren Schritt wiederverwendet.
Sei eine Grammatik G und ein Wort w = w0 ... wn-1 gegeben. Wir betrachten die Teilwörter wi,k von w, die an Position i beginnen und die Länge k haben, d.h. wi,k = wi ... wi+k-1.
Für jedes Teilwort wi,k ist ein Feld in der Tabelle vorgesehen; dort wird die Menge der Variablen Vi,k gespeichert, aus denen sich wi,k ableiten lässt (meist ist dies nur eine Variable, es können aber auch mehrere sein).
Die Tabelle wird spaltenweise berechnet. Die Variablenmengen Vi,1 in Spalte 1 bestehen aus den Variablen, aus denen sich das daneben befindliche Wort der Länge 1 ableiten lässt. So enthält beispielsweise V3,1 die Variable Y, weil sich b aus Y ableiten lässt (Bild 2 a).
Die Variablenmengen Vi,k in den anderen Spalten werden aus den schon gefüllten Feldern derselben Zeile und der darunter liegenden Diagonalen berechnet (Bild 2 b). Es werden die Produkte Vi,jVi+j,k-j gebildet. Enthält das Ergebnis die rechte Seite einer Produktion, so wird die zugehörige linke Seite in die Variablenmenge Vi,k aufgenommen.
So kommt beispielsweise die Variable S in die Variablenmenge V1,4, weil das Produkt V1,1V2,3 die rechte Seite der Produktion S XZ enthält.
XZ enthält.
Wenn zum Schluss im rechten oberen Eckfeld das Startsymbol S enthalten ist, so wird das Wort w erkannt, d.h. es gilt
w = w0, ..., wn-1 ∈ L(G) ⇔ S ∈ V0,n
Beispiel: Gegeben sei eine Grammatik G mit den Produktionen
| S |  | XY | XZ |
| Z |  | SY |
| X |  | a |
| Y |  | b |
und das Wort w = aaabbb. Der CYK-Algorithmus erzeugt folgende Tabelle:
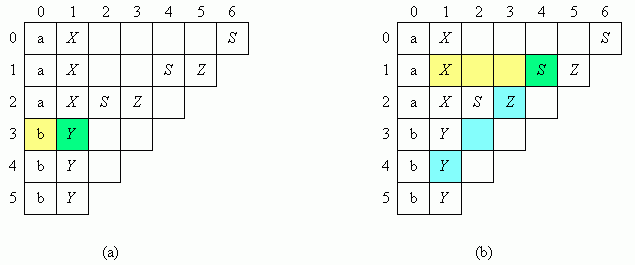
Bild 2: Tabelle des CYK-Algorithmus für die Grammatik G und das Wort w = aaabbb
Programm
Folgendes Programm implementiert den CYK-Algorithmus. Gegeben ist eine Grammatik G = (V, T, P, S) in Chomsky-Normalform und ein Wort w ∈ T * der Länge n. Gefragt ist, ob sich w in G ableiten lässt, ob also w ∈ L(G) ist.
Als Vorbereitung für den Algorithmus wird eine Tabelle mit n Zeilen und n+1 Spalten angelegt und in Spalte 0 zeichenweise das Wort w eingetragen.
Der Algorithmus benutzt die Funktion leftSidesOf(v), um die linken Seiten aller Produktionen zu ermitteln, die das in der Menge v befindliche Terminalzeichen als rechte Seite haben. Ferner benutzt er die Funktion leftSidesOfCombinationsOf(u, v), um die linken Seiten aller Produktionen mit der rechten Seite XY zu ermitteln, wobei X in der Menge u und Y in der Menge v enthalten ist.
CYK-Algorithmus
Eingabe:
Grammatik G in Chomsky-Normalform mit Startsymbol S,
n × n+1-Matrix V, in deren Spalte 0 ein Wort w der Länge n steht
Ausgabe:
true, falls w ∈ L(G), false sonst
Methode:
{
int i, j, k;
for (i=0; i<n; i++)
v[i][1]=g.leftSidesOf(v[i][0]);
for (k=2; k<=n; k++)
for (i=0; i<=n-k; i++)
for (j=1; j<k; j++)
v[i][k]+=g.leftSidesOfCombinationsOf(v[i][j], v[i+j][k-j]);
return v[0][n].contains("S");
}
Analyse
Der CYK-Algorithmus legt für ein Wort der Länge n eine Tabelle mit O(n2) Feldern an. Die Einträge in den Feldern werden in jeweils O(n) Schritten berechnet.
Der CYK-Algorithmus hat also eine Platzkomplexität von O(n2) und eine Zeitkomplexität von O(n3).
Literatur
[Web 1] http://de.wikipedia.org/wiki/CYK-Algorithmus Artikel in Wikipedia
Weiter mit: [Turing-Maschine] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 26.05.2008 Updated: 16.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden