Programmverifikation
Korrektheit von If-Else-Anweisungen
Die Schlussregel für die If-Else-Anweisung ergibt sich aus dem Flussdiagramm (Bild 1). Sie lautet
| {P ∧ B} S1 {Q}, {P ∧ ¬B} S2 {Q} |
| {P} if(B) S1 else S2 {Q} |
Um also {P} if(B) S1 else S2 {Q} zu beweisen, müssen {P ∧ B} S1 {Q} und {P ∧ ¬B} S2 {Q} bewiesen werden. In Bild 1 sind diese Vor- und Nachbedingungen in das Flussdiagramm der If-Else-Anweisung eingezeichnet.
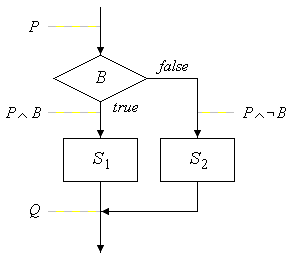
Bild 1: Vor- und Nachbedingungen bei der If-Else-Anweisung
Beispiel: Das folgende Programm berechnet das Maximum von zwei Werten a und b, das Ergebnis ist m.
m=a;
else
m=b;
Die Nachbedingung Q des Programms ist
Q: m = max(a, b)
Wir führen nun zwei getrennte Beweise für die beiden Prämissen, und zwar zunächst {P ∧ B} m=a; {Q} und dann {P ∧ ¬B} m=b; {Q} mit
B: a > b
Prämisse If1: If-Teil
Zuerst zeigen wir {P ∧ B} m=a; {Q}.
Der Beweis wird von unten nach oben geführt, unter Benutzung der Wertzuweisungsregel und der Konsequenzregel. Es stellt sich heraus, dass P: true die schwächste Vorbedingung für diesen Zweig ist.
| { P ∧ B } | (8) | |
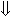 | { true ∧ a > b } | (7) |
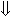 | { a > b } | (6) |
| { a > b ∨ a = b } | (5) | |
| { a ≥ b } | (4) | |
| { a = max(a, b) } | (3) | |
| m=a; | ||
| { m = max(a, b) } | (2) | |
| { Q } | (1) |
Die Konsequenzregel ermöglicht das Verschärfen von Bedingungen nach oben hin. Beim Übergang von Schritt (5) zu Schritt (6) haben wir davon Gebrauch gemacht und die Bedingung durch Weglassen einer Oder-Bedingung verschärft. Beim Übergang von Schritt (6) zu Schritt (7) haben wir die Bedingung durch Hinzufügen einer Und-Bedingung verschärft 1).
Prämisse If2: Else-Teil
Als nächstes zeigen wir {P ∧ ¬B} m=b; {Q}.
Auch hier ergibt sich P: true als schwächste Vorbedingung.
| { P ∧ ¬B } | (8) | |
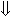 | { true ∧ ¬ a > b } | (7) |
| { ¬ a > b } | (6) | |
| { a ≤ b } | (5) | |
| { b ≥ a } | (4) | |
| { b = max(a, b) } | (3) | |
| m=b; | ||
| { m = max(a, b) } | (2) | |
| { Q } | (1) |
Nachdem wir diese beiden Beweise getrennt geführt haben, können wir aufgrund der Schlussregel für die If-Anweisung folgern
{ true } if (a>b) m=a; else m=b; { m = max (a, b) }
d.h. wir haben bewiesen, dass ohne irgendeine besondere Vorbedingung (außer der Bedingung true, die immer wahr ist) das Programm das Gewünschte tut.
Aufgaben
Aufgabe 1: Folgendes Programmstück ist gegeben:
{
h=a;
a=b;
b=h;
}
Geben Sie die schwächste Vorbedingung P für die Nachbedingung Q: a ≤ b an.
Aufgabe 2: Entwickeln Sie eine vereinfachte Schlussregel für die If-Anweisung ohne Else-Teil.
1) nur formal, nicht tatsächlich, denn (6) und (7) sind äquivalent
Weiter mit: [Korrektheit von While-Schleifen] [Literatur] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden