Programmverifikation
Semantikregeln
Wenn wir programmieren, wissen wir ungefähr, wie Programmanweisungen auszusehen haben, und wir haben auch eine Vorstellung davon, was sie bewirken. Tatsächlich jedoch gibt es formale Regeln, die sowohl die Struktur als auch die Bedeutung von Programmanweisungen exakt festlegen.
Definition: Die Syntax einer Programmiersprache ist die Gesamtheit der Regeln, die angeben, was ein Programm ist.
Definition: Die Semantik einer Programmiersprache ist die Gesamtheit der Regeln, die angeben, was ein Programm tut.
Die Syntax der Programmiersprache bestimmt also, welche Zeichenreihen vom Computer als gültiges Programm angesehen werden. Formal werden die Syntaxregeln im Wesentlichen durch eine Grammatik angegeben.
Die Semantik der Programmiersprache bestimmt, was der Computer macht, wenn er ein Programm ausführt. Formal werden die Semantikregeln beispielsweise durch die im Folgenden angegebenen Korrektheitsformeln (Hoare-Tripel – nach C.A.R. Hoare ) und darauf aufbauende Schlussregeln definiert [Hoa 69].
) und darauf aufbauende Schlussregeln definiert [Hoa 69].
Korrektheitsformeln
Die Semantik einer Programmiersprache wie Java enthält Regeln darüber, wie Ausdrücke ausgewertet werden, wie Anweisungen ausgeführt werden, wie Funktionsaufrufe behandelt werden und welche Auswirkungen die Deklaration von Variablen, Typen und Funktionen hat.
Wir beschränken uns auf die Semantik der grundlegenden Anweisungen. Die entsprechenden Semantikregeln werden im Folgenden definiert. Eine solche Regel ist entweder eine Korrektheitsformel der Form {P} S {Q} oder eine Schlussregel.
Definition: Die Korrektheitsformel {P} S {Q} ist wie folgt zu interpretieren: Wenn die Vorbedingung P vor Ausführung der Anweisung S gilt, so gilt nach der Ausführung der Anweisung S die Nachbedingung Q.
Die Bedingungen P und Q sind logische Formeln. Die Anweisung S kann auch eine zusammengesetzte Anweisung sein, z.B. eine strukturierte Anweisung wie eine Schleife oder ein Block von mehreren Anweisungen.
Die Schlussregeln sind Vorschriften, die angeben, wie aus vorhandenen Korrektheitsformeln oder logischen Formeln neue Korrektheitsformeln gebildet werden können. Die Schreibweise ist folgende:
| A1, ..., Ak |
| B |
Die Bedeutung einer solchen Schlussregel ist: Wenn A1, ..., Ak logische Formeln oder Korrektheitsformeln sind, so ist auch B eine Korrektheitsformel. Die über dem Strich stehenden Formeln heißen Prämissen, die unter dem Strich stehende Formel heißt Konklusion.
Es folgen die Semantikregeln für einige grundlegende Anweisungen der Programmiersprache Java; diese werden in den darauf folgenden Abschnitten erläutert.
Regeln
| {P[x←e]} x=e; {P} | (Wertzuweisungsaxiom) | ||||
| (Kompositionsregel) | ||||
| (Konsequenzregel / leere Anweisung) | ||||
| (If-Else-Regel) | ||||
| (While-Regel) | ||||
Wertzuweisungsaxiom
Von grundlegender Bedeutung ist die Regel für die Wertzuweisung. Sie gibt die schwächste Vorbedingung an, die vor der Zuweisung x=e; gilt, wenn als Nachbedingung P gilt. Hierbei ergibt sich die Vorbedingung P[x←e], indem in der Nachbedingung P alle freien Vorkommen der Variablen x durch den Ausdruck e ersetzt werden.
Beispiel: Es gilt
{ x+1 = 3 } x=x+1; { x = 3 }
In der Nachbedingung P: x = 3 kommt x als freie Variable vor. Wird in P die Variable x durch den Ausdruck x+1 ersetzt, so ergibt sich die Vorbedingung x+1 = 3.
Diese Bedingung lässt sich durch die äquivalente Bedingung x = 2 ersetzen – formal werden hierfür jedoch die Kompositionsregel und die Konsequenzregel benötigt (siehe Beispiel weiter unten).
Da die Vorbedingung sich aus der Nachbedingung ergibt, werden Programme "von unten nach oben" bewiesen. Der fertige Beweis wird dann von oben nach unten gelesen.
Kompositionsregel
Die Regel für die Komposition, also für die Hintereinanderausführung von Anweisungen, wird gebraucht, um einen Beweis für ein Programm Schritt für Schritt führen zu können. Zwischen je zwei Anweisungen steht eine Bedingung Q, die Nachbedingung der einen und zugleich Vorbedingung der anderen Anweisung ist. Eine solche Bedingung, die in geschweiften Klammern an bestimmter Stelle im Programm steht, wird als Zusicherung (engl.: assertion) bezeichnet.
Beispiel: In folgendem Programm werden die Werte der Variablen a und b vertauscht. Der Beweis wird von unten nach oben geführt. Es wird dreimal das Wertzuweisungsaxiom angewendet. Als erstes werden in der Zusicherung (1) alle (freien) Vorkommen der Variablen b, die auf der linken Seite der Wertzuweisung b=h; steht, durch die rechte Seite h ersetzt. Das Ergebnis ist die Zusicherung (2). Dann werden in (2) alle Vorkommen von a durch b ersetzt, und schließlich in (3) alle Vorkommen von h durch a.
| { b = A ∧ a = B } | (4) | |
| h=a; | ||
| { b = A ∧ h = B } | (3) | |
| a=b; | ||
| { a = A ∧ h = B } | (2) | |
| b=h; | ||
| { a = A ∧ b = B } | (1) |
Insgesamt gilt also
{ b = A ∧ a = B } h=a; a=b; b=h; { a = A ∧ b = B },
d.h. wenn vor Ausführung des Programms die Variable b den Wert A und die Variable a den Wert B hat, dann hat nach Ausführung des Programms a den Wert A und b den Wert B. Die Werte werden also vertauscht.
Konsequenzregel
Die Konsequenzregel besagt Folgendes: Falls Q Nachbedingung der leeren Anweisung ist, so ist jede Bedingung P als Vorbedingung gültig, für die gilt P⇒Q. Die Konsequenzregel erlaubt es also, in Verbindung mit der Kompositionsregel, im Beweis eines Programms Bedingungen nach oben hin zu verschärfen. Insbesondere erlaubt sie auch, Bedingungen durch äquivalente Bedingungen zu ersetzen.
Beispiel: Zu zeigen ist
{ x > 0 } x=x+1; { x > 0 }
Der Beweis wird von unten nach oben geführt.
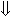 | { x > 0 } | (3) |
| { x+1 > 0 } | (2) | |
| x=x+1; | ||
| { x > 0 } | (1) |
Der Übergang zwischen Bedingung (2) und Bedingung (3) ergibt sich aufgrund der Konsequenzregel, denn es gilt
x > 0 ⇒ x+1 > 0
Zwischen (2) und (3) steht eine leere Anweisung.
Bemerkung: Da wir den Beweis von unten nach oben führen, ergeben sich die Bedingungen, die wir mithilfe der Konsequenzregel entwickeln, entgegen der Richtung unseres gewohnten logischen Schließens. Wir argumentieren gewissermaßen in Gegenrichtung des ⇒-Pfeils. Dies ist zunächst gewöhnungsbedürftig und manchmal auch fehlerträchtig.
Bei äquivalenten Umformungen, wie in dem folgenden Beispiel, haben wir kein Problem. Ansonsten aber hilft es, wenn wir uns merken, dass wir Bedingungen nach oben hin verschärfen dürfen.
Insbesondere werden wir häufig Bedingungen dadurch verschärfen, dass wir Und-Bedingungen hinzufügen oder Oder-Bedingungen weglassen.
Beispiel: Zu beweisen ist die Korrektheitsformel aus dem Beispiel zum Wertzuweisungsaxiom:
{ x = 2 } x=x+1; { x = 3 }
Der Beweis wird von unten nach oben geführt.
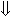 | { x = 2 } | (3) |
| { x+1 = 3 } | (2) | |
| x=x+1; | ||
| { x = 3 } | (1) |
Der Übergang zwischen Bedingung (2) und Bedingung (3) ergibt sich aufgrund der Konsequenzregel, denn es gilt
x = 2 ⇔ x+1 = 3
Zwischen (2) und (3) steht eine leere Anweisung.
Die Schlussregeln für die If-Else-Anweisung und für die While-Schleife werden auf den folgenden Seiten erläutert.
Aufgaben
Aufgabe 1: Beweisen Sie
| { x < y } | |
| x=y-x; | |
| x=y+x; | |
| { y < x } |
Weiter mit: [Korrektheit von If-Else-Anweisungen] [Literatur] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden