Mathematik
Abbildung, Funktion
Definition
Eine Abbildung ist eine Menge von Paaren (x, y), wobei x aus einer Menge X und y aus einer Menge Y stammt.
Wenn es sich um Zahlenpaare handelt, so sind die Mengen X und Y meist die reellen Zahlen ℝ. Dann spricht man statt von einer Abbildung auch von einer Funktion.
Nun ist allerdings nicht jede Menge von Paaren (x, y) eine Abbildung. Es müssen zwei Bedingungen erfüllt sein:
| 1) | Für jedes Element x aus X gibt es mindestens ein Paar (x, y) | |
| 2) | Für jedes Element x aus X gibt es höchstens ein Paar (x, y) |
Zusammengenommen ergeben diese beiden Bedingungen
| 1+2) | Für jedes Element x aus X gibt es genau ein Paar (x, y) |
Jede Menge von Paaren, die diese beiden Bedingungen 1 und 2 erfüllt, ist eine Abbildung.
Die Vorstellung bei einer Abbildung ist, dass jeweils x auf y abgebildet wird. Die Bedingungen besagen, dass jedes x aus X auf genau ein y abgebildet werden muss. Es darf kein x geben, das überhaupt nicht abgebildet wird, und es darf kein x geben, das auf mehrere verschiedenene y abgebildet wird.
Bildlich dargestellt werden kann ein Paar (x, y) durch einen Pfeil von x nach y (Bild 1).
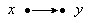
Bild 1: Element x wird auf Element y abgebildet
In Bild 2 sind Situationen dargestellt, die bei einer Abbildung nicht auftreten dürfen. Das Element x0 aus der Menge X wird nicht abgebildet, und das Element x1 aus der Menge X wird auf zwei verschiedene Elemente abgebildet.
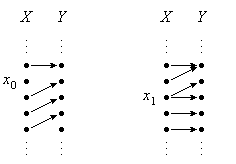
Bild 2: Nicht zulässige Situationen bei einer Abbildung von X nach Y
Auf die bildliche Darstellung bezogen lassen sich die beiden Bedingungen für eine Abbildung wie folgt formulieren:
| 1) | Von jedem Element von X muss mindestens ein Pfeil ausgehen | |
| 2) | Von jedem Element von X darf höchstens ein Pfeil ausgehen |
Zusammengenommen ergibt dies
| 1+2) | Von jedem Element von X muss genau ein Pfeil ausgehen |
Über die Elemente von Y wird nichts gesagt. Es kann Elemente von Y geben, bei denen kein Pfeil ankommt, und es kann Elemente von Y geben, bei denen mehrere Pfeile ankommen. Dies ist zulässig und auch typisch für Abbildungen im Allgemeinen.
Benennung
Da es verschiedene Abbildungen bzw. Funktionen gibt, ist es erforderlich, sie zu benennen, um sie auseinanderhalten zu können.
In der Praxis stößt du auf Benennungen wie
- die Funktion y = f(x)
- die Funktion y = x2
- die Abbildung ℕ → ℕ mit n ↦ n+1
Du erinnerst dich, dass eine Abbildung bzw. Funktion eine Menge von Paaren ist. Welche Mengen von Paaren werden nun durch die oben bezeichneten Abbildungen dargestellt?
Der erste Fall besagt nichts anderes, als dass eine bestimmte Menge von Paaren (x, y) mit f bezeichnet wird:
f = { (x, y) }
Um welche Paare genau es sich handelt, wird hierbei nicht gesagt. Die Schreibweise y = f(x) ist gleichbedeutend mit (x, y) ∈ f.
Im zweiten Fall ist eine konkrete Menge von Paaren gemeint, nämlich die Menge aller Paare (x, y) mit der Eigenschaft, dass y = x2 ist:
{ (x, y) | y = x2 }
Diese Menge enthält z.B. die Paare (3, 9), (4, 16), aber auch (-5, 25), (0, 0), (1.5, 2.25), (0.1, 0.01), ( 2, 2), ..., insgesamt unendlich viele.
2, 2), ..., insgesamt unendlich viele.
Im dritten Fall ist die Menge aller Paare (n, n+1) mit n ∈ ℕ gemeint:
{ (n, n+1) } = { (1, 2), (2, 3), (3, 4), ... }
Wichtig ist, so unterschiedlich die Bezeichnungsweisen auch sein mögen, dass du dir immer wieder Folgendes klarmachst:
Eine Funktion ist immer eine Menge von Paaren, und nichts anderes.
D.h. wenn etwa gesagt wird, dass y = x2 eine Funktion sei, so stimmt dies genau genommen nicht, sondern y = x2 ist die Funktionsgleichung der Funktion. Die Funktion selber ist die Menge aller Zahlenpaare (x, y), welche die Funktionsgleichung erfüllen.
Wertetabelle
Eine Wertetabelle einer Funktion ist eine Auflistung genau dieser Zahlenpaare (x, y) der Funktion. Da es aber meistens unendlich viele dieser Zahlenpaare gibt, werden in die Wertetabelle nur einige davon aufgelistet. Als Beispiele sind hier Wertetabellen für die Abbildungen n↦n+1 und y = x2 angegeben.
|
|
Bild 3: Wertetabellen für zwei Funktionen
Grafische Darstellung von Funktionen
In einem Koordinatenkreuz entspricht jedem Zahlenpaar (x, y) ein Punkt.
Eine Funktion ist eine Menge von Zahlenpaaren. Um die Funktion grafisch darzustellen, zeichnest du für jedes dieser Zahlenpaare den entsprechenden Punkt in die Zeichenebene des Koordinatenkreuzes.
Um beispielsweise die Funktion mit der Funktionsgleichung y = x2 grafisch darzustellen, zeichnest du einen Punkt für das Zahlenpaar (3, 9), einen für (4, 16), weitere für (-5, 25), (0, 0), (1.5, 2.25), (0.1, 0.01), ( 2, 2) usw. – insgesamt unendlich viele. Da die Punkte sehr dicht beieinanderliegen, entsteht eine Linie oder Kurve (Bild 4).
2, 2) usw. – insgesamt unendlich viele. Da die Punkte sehr dicht beieinanderliegen, entsteht eine Linie oder Kurve (Bild 4).
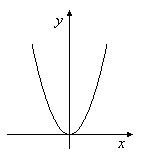
Bild 4: Grafische Darstellung der Funktion mit der Gleichung y = x2
Die meisten in der Praxis vorkommenden Funktionen ergeben in der grafischen Darstellung derartige Kurven. Die Definition des Begriffs Funktion verlangt jedoch nicht, dass die Funktion sich als Kurve darstellen lässt. Tatsächlich können die Punkte, die den Zahlenpaaren der Funktion entsprechen, genauso gut wirr über die Zeichenebene verteilt sein. Ein Beispiel ist die Dirichlet -Funktion d:
-Funktion d:
| d(x) = |  |
|
Weiter mit: [Stetigkeit] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 19.12.2000 Updated: 20.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden