Mathematik
Stetigkeit
Intervall
Ein Intervall ist eine zusammenhängende Teilmenge von ℝ. Anschaulich ist ein Intervall eine zusammenhängende Menge von Punkten auf der Zahlengeraden (Bild 1).
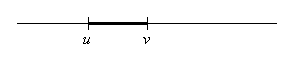
Bild 1: Ein Intervall
Definition: Seien u, v ∈ ℝ. Dann sind folgende Mengen Intervalle:
(u, v) = { x | u < x < v }
[u, v] = { x | u ≤ x ≤ v }
[u, v) = { x | u ≤ x < v }
(u, v] = { x | u < x ≤ v }
Das erste Intervall ist ein offenes Intervall, das zweite Intervall ist ein abgeschlossenes Intervall. Die anderen beiden Intervalle sind halboffene Intervalle.
Umgebung
Definition: Sei z ∈ ℝ. Ein offenes Intervall A = (u, v) mit z ∈ A heißt offene Umgebung von z.
Eine Menge U heißt Umgebung von z, wenn sie eine offene Umgebung von z enthält.
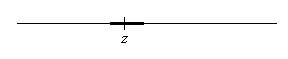
Bild 2: Eine Umgebung von z
Eine Umgebung von z besteht also aus einer offenen Umgebung von z plus möglicherweise noch weiteren Elementen.
Bild einer Menge
Definition: Sei f : D → ℝ eine Funktion mit dem Definitionsbereich D ⊆ ℝ.
Sei A ⊆ ℝ. Das Bild f(A) dieser Menge ist wie folgt definiert:
f(A) = { f(x) | x ∈ A ∩ D }.
Die Menge f(A) besteht also aus den Bildern aller Elemente x ∈ A, aber natürlich nur, soweit diese x auch im Definitionsbereich der Funktion liegen (Bild 3).
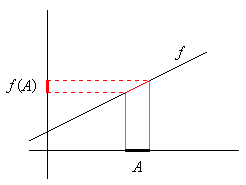
Bild 3: Bild der Menge A
Stetigkeit
Sei wiederum f : D → ℝ und x ∈ D, also ein Punkt auf der x-Achse, der im Definitionsbereich der Funktion liegt. Wir definieren nun, wann die Funktion stetig im Punkt x ist.
Definition: Die Funktion f ist stetig im Punkt x, wenn zu jeder (beliebig kleinen) Umgebung B um f(x) es eine Umgebung A um x gibt mit
f(A) ⊆ B.
Folgendes Bild 4 zeigt links eine Funktion, die im Punkt x stetig ist. Ganz gleich wie die Umgebung B gewählt wird, immer gibt es eine Umgebung A, derart dass f(A) innerhalb von B liegt (rot gekennzeichnet).
Rechts ist eine Funktion dargestellt, die im Punkt x nicht stetig ist. Zur dargestellten Umgebung B gibt es keine Umgebung A, ganz gleich wie klein diese auch gewählt wird, derart dass f(A) innerhalb von B liegt. Immer liegt ein Teil von f(A) außerhalb von B.
Wichtig ist hierbei, dass die Umgebung A eine offene Umgebung enthält – die Umgebung um x darf nicht ein Intervall (u, x] sein, das bei x abgeschlossen ist.
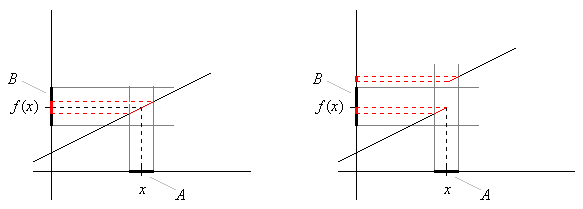
Bild 4: In x stetige Funktion (links) und in x nicht stetige Funktion (rechts)
Definition: Eine Funktion heißt stetig, wenn sie in jedem Punkt ihres Definitionsbereichs stetig ist.
Die meisten Funktionen, die als Kurven gezeichnet werden können, sind stetig. Es gibt aber auch Funktionen, die nirgendwo stetig sind.
Beispiel: Die Dirichlet
-Funktion d mit
| d(x) = |  |
|
ist in jedem Punkt unstetig.
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 17.05.2003 Updated: 20.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden