Dreisatz
Dreisatz (umgekehrte Proportionalität)
Problem
Um einen Graben auszuheben, brauchen 3 Arbeiter 10 Stunden. Wie lange brauchen 5 Arbeiter?
Du löst dieses Problem in 5 Schritten.
Ansatz
Schritt 1
Als Erstes schreibst du die Zahlen in ein Schema:
| 3 | Arbeiter brauchen | 10 | Stunden | |||
| 5 | Arbeiter brauchen | x | Stunden |
Der Buchstabe x steht für die unbekannte, die gesuchte Zahl.
Wichtig ist dabei, dass jeweils gleiche Größen übereinander stehen: Arbeiter müssen über Arbeitern stehen, Stunden müssen über Stunden stehen.
Da es nur auf die Zahlen ankommt, schreibst du dasselbe Schema nur mit Zahlen:
| 3 | 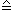 | 10 | ||
| 5 | 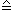 | x |
Das Zeichen 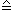 bedeutet "entspricht".
bedeutet "entspricht".
Lösung
Schritt 2
Als Nächstes stellst du fest, ob die beiden Größen, nämlich Arbeiter und Stunden, in direkt proportionalem oder in umgekehrt proportionalem Verhältnis zueinander stehen. Hier sind die beiden Größen umgekehrt proportional zueinander: je mehr Arbeiter, desto weniger Stunden.
Schritt 3
Bei umgekehrter Proportionalität muss jeweils dasselbe herauskommen, wenn du waagerecht multiplizierst. Das Produkt der beiden gelb markierten Zahlen muss gleich dem Produkt der beiden blau markierten Zahlen sein:
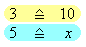
Bild 1: Multiplikation bei umgekehrter Proportionalität
In diesem Beispiel muss also gelten:
3 · 10 = 5 · x .
Das Ergebnis, die gesuchte Zahl x, findest du, indem du die Gleichung nach x auflöst:
| 3 · 10 |
| 5 |
Den Bruch kannst du kürzen, das Ergebnis ist 6:
x = 3 · 2 = 6
Schritt 4
Du drückst die Lösung in Worten aus, als Antwort auf die Frage, die in der Aufgabe gestellt ist:
"Zum Ausheben des Grabens brauchen 5 Arbeiter 6 Stunden."
Probe
Schritt 5
Zur Probe schaust du ganz grob, ob das Ergebnis richtig sein kann. Da 5 Arbeiter fast doppelt so viele sind wie 3 Arbeiter, brauchen sie nur etwas mehr als halb so lange. Tatsächlich sind 6 Stunden etwas mehr als die Hälfte von 10 Stunden. Du hast also wohl richtig gerechnet!
Weiter mit: [Mehrfache Proportionalität] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 09.01.2005 Updated: 20.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden