Kryptografische Protokolle

Bei einem symmetrischen Verschlüsselungsverfahren benötigt der Empfänger denselben Schlüssel, mit dem der Sender die Nachricht verschlüsselt hat. Bei einem asymmetrischen Verschlüsselungsverfahren benötigt der Sender den öffentlichen Schlüssel des Empfängers, um die Nachricht zu verschlüsseln. Bei dem folgenden Verfahren können Nachrichten sogar ohne gemeinsamen Schlüssel und ohne öffentlichen Schlüssel verschlüsselt werden.

Zu Beginn tauschen A und B öffentlich eine Primzahl p aus.

A		C		B
		Primzahl p
erzeugt    a und a' mit    aa' ≡ 1 (mod p-1)				erzeugt    b und b' mit    bb' ≡ 1 (mod p-1)
berechnet    x = m a mod p
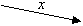				berechnet    y = x b mod p
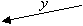berechnet    z = y a' mod p
				berechnet    w = z b' mod p

Nach dem Satz von Euler gilt für alle m < p und für alle k ∈ ℕ₀

m^k·φ(p)+1  =  m.

Da p Primzahl, gilt φ(p) = p-1, und damit ist aa' = k·φ(p)+1; entsprechendes gilt für bb'. Somit gilt (modulo p gerechnet)

w = z ^b' = y ^{a' b'} = x ^{ba' b'} = m ^{aba' b'} = m ^{aa' bb'} = m

d.h. die Nachricht m kommt beim Empfänger B an.

Aus der Kenntnis von x, y und z sowie p kann jedoch m nicht berechnet werden, jedenfalls nicht mit vertretbarem Aufwand (Problem des diskreten Logarithmus).

Eine Angriffsmöglichkeit besteht darin, dass B durch C simuliert wird (Man-in-the-Middle-Attack).

Literatur

[BSW 95]   A. Beutelspacher, J. Schwenk, K.D. Wolfenstetter: Moderne Verfahren der Kryptographie. Vieweg (1995)

[Lan 18]   H.W. Lang: Kryptografie für Dummies. Wiley (2018)

[Weitere Informationen]