Post-Quanten-Kryptografie
LWE-Verschlüsselung
Zugrundegelegt ist ein Gitter L, das in den Raum ℤqm eingebettet ist. Hierbei ist q eine Primzahl, alle Berechnungen werden modulo q durchgeführt. Das Gitter wird durch n Basisvektoren a0, ..., an-1 ∈ ℤqm beschrieben; diese werden zu einer m×n-Matrix A zusammengefasst.
Das Learning-With-Errors-Problem (LWE)
Auf Grundlage eines Gitters erhalten Sie das sogenannte Learning-With-Errors-Problem (LWE):
Definition: (LWE-Problem)
Gegeben ist eine Matrix A von n Basisvektoren ai ∈ ℤqm und ein Punkt t ∈ ℤqm.
Gesucht ist der Lösungsvektor s ∈ ℤqn des Gleichungssystems
A · s + e = t
wobei e ∈ ℤqm ein unbekannter Fehlervektor ist.
Verschlüsseln mit LWE
Im Folgenden bezeichnet der Buchstabe m neben der Dimension des Vektorraums, in den das Gitter L eingebettet ist, auch wie üblich den Klartext (message) – aus dem Zusammenhang wird die unterschiedliche Verwendung klar.
Öffentlichen und privaten Schlüssel erzeugen
Mit folgenden Schritten erzeugen Sie als Empfänger einen öffentlichen Schlüssel und einen zugehörigen privaten Schlüssel.
Schlüssel erzeugen
Ausgabe:
Öffentlicher Schlüssel (t, A) und privater Schlüssel s
Methode:
- Wähle n zufällige Spaltenvektoren ai ∈ ℤqm und bilde daraus die Matrix A = [a0, ..., an-1].
- Erzeuge einen zufälligen geheimen Schlüssel s ∈ ℤqn, wobei dessen Komponenten si relativ "kleine" Werte sind, zum Beispiel |si| ≤ q div 8.
- Erzeuge einen zufälligen Fehlervektor e ∈ ℤqm, ebenfalls mit "sehr kleinen" Werten, zum Beispiel aus der Menge {-1, 0 , 1}.
- Berechne t = A · s + e.
- Gib (t, A) als öffentlichen Schlüssel und s als privaten Schlüssel zurück.
Die Wahrscheinlichkeit ist sehr groß, dass die zufällig gewählten Basisvektoren a0, ..., an-1 tatsächlich linear unabhängig sind.
Verschlüsseln und entschlüsseln
Ein Sender verschlüsselt den Klartext m mit dem öffentlichen Schlüssel des Empfängers. Im einfachsten Fall besteht im Folgenden der Klartext nur aus einem einzigen Bit. d.h. m ∈ {0, 1}.
Der beim Verschlüsseln erzeugte Geheimtext besteht aus zwei Teilen: dem verschlüsselten Bit c und einem Hilfsvektor h. Etwas Ähnliches haben Sie bereits beim Verschlüsselungsverfahren von ElGamal gesehen. Auch dort benötigt der Empfänger außer dem eigentlichen Geheimtext noch einen zusätzlichen Wert zum Entschlüsseln.
Bild 1 zeigt den Ablauf des LWE-Verschlüsselungsverfahrens.
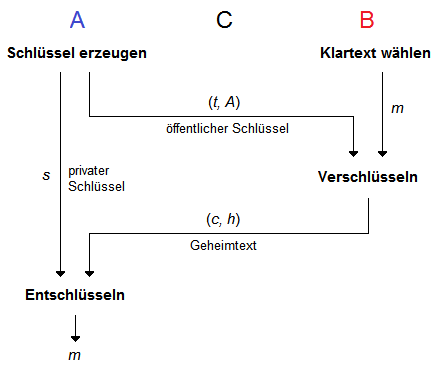
Bild 1: Ablauf des LWE-Verschlüsselungsverfahrens
Vor dem eigentlichen Verschlüsseln wird das Bit m zunächst in eine Zahl m' ∈ ℤq codiert. Später nach dem Entschlüsseln wird diese Zahl wieder zurück in ein Bit dekodiert.
Bits codieren
Um einen Klartext m ∈ {0, 1} zu codieren, bilden Sie zunächst mithilfe einer Abbildung c die Menge {0, 1} in die Menge ℤq = {0, ..., q-1} ab, und zwar durch
| m' = c(m) = m · q div 2 = |  |
|
Hierbei bedeutet div die ganzzahlige Division. Beispielsweise bilden Sie für q = 17 die 0 auf die 0 und die 1 auf die 8 ab.
Zum Dekodieren bilden Sie mit einer Abbildung d alle q div 2 Zahlen aus ℤq, die zu 0 benachbart sind, zurück auf die 0 ab, und alle restlichen Zahlen, die zu q div 2 benachbart sind, zurück auf die 1.
| m = d(m') = |  |
|
Für q = 17 sind die Zahlen -4, ..., 3 zu 0 benachbart; die restlichen Zahlen 4, ..., 12 sind zu 8 benachbart. Da q ungerade ist, hat die 8 einen Nachbarn mehr als die 0. Bild 2 zeigt anschaulich diese Zuordnung.
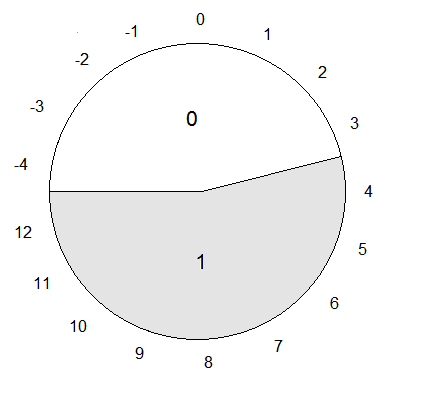
Bild 2: Zuordnung der Zahlen aus ℤ17 zu 0 und 1
Im Folgenden bezeichnet AT die Transponierte der Matrix A. Durch Transposition einer m×n-Matrix erhalten Sie eine n×m-Matrix, deren Zeilen gleich den Spalten der ursprünglichen Matrix sind. Entsprechend entsteht durch Transposition aus einem Spaltenvektor ein Zeilenvektor und umgekehrt.
Verschlüsseln
Eingabe:
Öffentlicher Schlüssel (t, A) des Empfängers, Klartext m ∈ {0, 1}
Ausgabe:
Geheimtext (c, h) mit c ∈ ℤq und h ∈ ℤqn
Methode:
- Codiere das Klartextbit m durch m' = c(m) ∈ ℤq.
- Wähle zufällige kleine Werte und bilde daraus Vektoren r ∈ ℤqm und e ∈ ℤqn, wähle zudem einen kleinen Wert e'.
- Berechne h = AT · r + e.
- Berechne c = tT · r + e' + m'.
- Gib den Geheimtext (c, h) zurück.
Entschlüsseln
Eingabe:
Privater Schlüssel s ∈ ℤqn des Empfängers, Geheimtext (c, h)
Ausgabe:
Klartextbit m ∈ {0, 1}
Methode:
- Berechne m' = c – sT·h.
- Dekodiere m' und gib das Ergebnis m = d(m') zurück.
Beispiel mit kleinen Zahlen
Anhand des folgenden Beispiels vollziehen Sie den Gang der Berechnungen mit kleinen Zahlen nach. Das Gitter L hat den Rang n = 3, es ist eingebettet in den m-dimensionalen Raum ℤqm, hierbei ist m = 5. Die Zahl q ist gleich 17.
Schlüssel erzeugen
In Schritt 1 erzeugen Sie n = 3 zufällige Spaltenvektoren der Länge m = 5 mit Komponenten aus ℤ17 und bilden daraus die Matrix A:
| A = |  |
|  |
In Schritt 2 erzeugen Sie den Vektor s ∈ ℤq3 und den Fehlervektor e ∈ ℤq5 aus "kleinen" Werten:
|
|
Dann berechnen Sie in Schritt 3, jeweils immer modulo 17
|
|
|
|
Nun haben Sie den öffentlichen Schlüssel (t, A) und den privaten Schlüssel s erhalten.
Verschlüsseln
Angenommen, Sie wollen das Bit m = 1 verschlüsseln.
Zunächst codieren Sie in Schritt 1 das Klartextbit m = 1 durch m' = c(m) = 17 div 2 = 8.
Dann bilden Sie in Schritt 2 die Vektoren r und e sowie den Wert e'.
|
| e' = -1 |
In Schritt 3 berechnen Sie
|
|
|
|
In Schritt 4 berechnen Sie
| c = tT · r + e' + m' = [ 9 6 8 14 7 ] |
| + (-1) + 8 = 6 |
Nun senden Sie den Geheimtext (c, h) = (6, [7 0 13]T) an den Empfänger.
Entschlüsseln
Als Empfänger berechnen Sie
| m' = c – sT·h = 6 – [-2 1 1] |
| = 7 |
Dann dekodieren Sie m' = 7 zu m = d(7) = 1 und erhalten so das Klartextbit m = 1 zurück.
Sicherheit
Wenn Sie als Angreifer aus dem öffentlichen Schlüssel (t, A) den privaten Schlüssel s berechnen wollen, müssen Sie die Gleichung
A · s + e = t
lösen. Dies entspricht genau dem LWE-Problem. Ein LWE-Problem mit geeignet gewählten Parametern zu lösen, gilt jedoch als undurchführbar, sowohl mit einem konventionellen Digitalcomputer als auch mit einem Quantencomputer.
Entsprechendes gilt, wenn Sie als Angreifer den Klartext direkt aus dem Geheimtext berechnen wollen.
Bewertung des Verfahrens
- Der Geheimtext, der durch Verschlüsselung nur eines einzigen Bits entsteht, erreicht eine beträchtliche Länge, insbesondere dann, wenn das Verfahren mit realistischen Parametern angewendet wird.
- Es ist natürlich zu wenig, nur ein einziges Bit zu verschlüsseln. Gebraucht wird ein Verfahren, das eine längere Bitfolge verschlüsseln kann.
- Auch ist die Datenmenge zu groß, die für den öffentlichen Schlüssel erforderlich ist, immerhin eine m×n-Matrix, wobei in realistischen Anwendungen die Dimensionen m und n in die Hunderte gehen können.
Literatur
Die hier gewählte Darstellung folgt dem Buch
[PPG 24] C. Paar, J. Pelzl, T. Güneysu: Understanding Crytography. 2. Auflage, Springer (2024)
Weiter mit: [Ring-LWE-Verschlüsselung] oder [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 29.01.2025 Updated: 25.06.2025
Diese Webseiten sind größtenteils während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden