Kryptografie
Klassische Kryptografie
Symmetrische Verschlüsselung
Ein Sender möchte einem Empfänger eine geheime Nachricht übermitteln. Dabei soll sichergestellt werden, dass nur der legitime Empfänger Kenntnis vom Inhalt der Nachricht erhält, aber kein unberechtigter Dritter, der die Nachricht abfängt oder abhört.
Die klassische Kryptografie löst dieses Problem dadurch, dass der Sender den Klartext m mithilfe einer zusätzlichen Information, des Schlüssels k, in einen Geheimtext c umcodiert (chiffriert, verschlüsselt). Mithilfe des Schlüssels kann den Geheimtext wieder entschlüsselt (dechiffriert) und der Klartext zurückgewonnen werden.
Voraussetzungen für eine geheime Übermittlung sind also, dass
- der Empfänger den Schlüssel kennt, den der Sender verwendet hat,
- niemand sonst den Schlüssel kennt,
- es ohne Kenntnis des Schlüssels unmöglich oder zumindest außerordentlich schwierig ist, den Klartext zurückzugewinnen.
Die Schwierigkeiten liegen darin, dass Sender und Empfänger
- einen gemeinsamen Schlüssel vereinbaren müssen, bevor sie geheime Botschaften austauschen können,
- den Schlüssel geheimhalten müssen und
- ein sicheres Verschlüsselungsverfahren finden müssen.
Das folgende Bild 1 zeigt schematisch die Verschlüsselung eines Klartextes m durch einen Algorithmus f mit Schlüssel k. Der Klartext und der Schlüssel sind geheim, der Algorithmus und der erzeugte Geheimtext c sind im Prinzip öffentlich zugänglich. Um den Geheimtext wieder zu entschlüsseln, muss der Empfänger den Algorithmus f und den Schlüssel k kennen, um einen entsprechenden Entschlüsselungsalgorithmus fk' anwenden zu können.
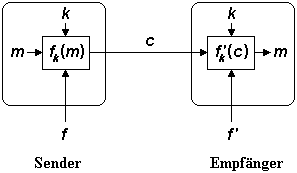
Bild 1: Verschlüsseln und Entschlüsseln
Monoalphabetische Verschlüsselung
Sei A ein Alphabet; im Folgenden sei A das Alphabet der 26 Buchstaben A, ..., Z. Die einfachste Form der Verschlüsselung besteht darin, jeden Buchstaben des Alphabets durch einen bestimmten anderen Buchstaben zu ersetzen. Dies bezeichnet man als monoalphabetische Verschlüsselung.
Caesar-Chiffre
Gegeben sei der Klartext ABENDZEIT. Bei der Caesar-Chiffre wird jeder Buchstaben des Klartextes durch z.B. den übernächsten Buchstaben im Alphabet ersetzt (gemäß der alphabetischen Reihenfolge und zyklisch, d.h. auf Z folgt wieder A). Das Ergebnis ist der Geheimtext CDGPFBGKV.
Mathematisch entspricht diese Verschlüsselung einer buchstabenweisen "Addition" des Textes CCCCCCCCC zum Klartext. Werden die Buchstaben entsprechend der alphabetischen Reihenfolge von 0 bis 25 nummeriert, so ergibt sich die Summe zweier Buchstaben aus der Summe dieser Nummern modulo 26.
Der Empfänger kann aus dem Geheimtext den Klartext wieder zurückgewinnen. Er muss dazu wissen, mit welchem Algorithmus die Verschlüsselung vorgenommen wurde (hier: Addition), und er muss den Schlüssel C kennen. Durch Umkehrung des Verschlüsselungsalgorithmus (hier: Subtraktion) unter Verwendung des richtigen Schlüssels ergibt sich wieder der Klartext.
Mithilfe einer Chiffrierscheibe, die auf den Schlüssel, also z.B. auf C eingestellt wird, lassen sich in sehr bequemer Weise Texte verschlüsseln und wieder entschlüsseln [Beu 97].
Kryptanalyse
Die Entschlüsselung des Geheimtextes ohne Kenntnis des Schlüssels bezeichnet man als Kryptanalyse.
Im einfachsten Fall gelingt die Kryptanalyse durch Ausprobieren aller Möglichkeiten. Im Falle der Caesar-Chiffre gibt es nur 26 verschiedene Schlüssel. Woher will man aber wissen, dass k = C und der Klartext ABENDZEIT, nicht jedoch k = D und der Klartext ZADMCYDHS ist? Dies liegt offenbar an der Redundanz der natürlichen Sprache. In natürlicher Sprache sind nicht alle Zeichenfolgen gleich wahrscheinlich, sondern die Zeichenfolge ABENDZEIT ist z.B. sehr viel wahrscheinlicher als ZADMCYDHS.
Hieraus ergibt sich ein Ansatzpunkt, um komplizierter verschlüsselte Texte zu entziffern. Wählt man für den Algorithmus f anstelle einer Verschiebung um i Symbole im Alphabet eine beliebige Permutation des Alphabets, so gibt es hierfür 26!  1026 Möglichkeiten; diese lassen sich nicht mehr alle ausprobieren. Aber aufgrund der Tatsache, dass in deutschen Klartexten E der häufigste Buchstabe ist, findet man sehr schnell f(E), nämlich den häufigsten Buchstaben im Geheimtext. Der nächsthäufigste Buchstabe ist N, dann folgen I, S, R, A, T. Hat man die Entsprechungen dieser Buchstaben gefunden, so kann man den Klartext meist schon erraten (A_EN__EIT).
1026 Möglichkeiten; diese lassen sich nicht mehr alle ausprobieren. Aber aufgrund der Tatsache, dass in deutschen Klartexten E der häufigste Buchstabe ist, findet man sehr schnell f(E), nämlich den häufigsten Buchstaben im Geheimtext. Der nächsthäufigste Buchstabe ist N, dann folgen I, S, R, A, T. Hat man die Entsprechungen dieser Buchstaben gefunden, so kann man den Klartext meist schon erraten (A_EN__EIT).
Kann für die Kryptanalyse lediglich der Geheimtext herangezogen werden, wird dies als
ciphertext-only-attack
bezeichnet. Ist die Situation gegeben, dass auch ein Teil des Klartextes bekannt ist, so ist dies eine
known-plaintext-attack
Häufig ist es auch möglich, den Klartext zu erraten. So ist es z.B. wahrscheinlich, dass in einem militärischen Text das Wort "Befehl" vorkommt oder dass eine private E-Mail mit "Hallo" anfängt.
Im Falle der Caesar-Chiffre genügt die Kenntnis eines einzigen Klartextzeichens zusammen mit dem entsprechenden Geheimtextzeichen, um den Schlüssel k bestimmen zu können. Bei Verschlüsselung mit einer beliebigen Permutation benötigt man einen Klartext, in dem die wichtigsten Buchstaben mindestens einmal vorkommen. Dann kann man die Zuordnung zu den entsprechenden Geheimtextzeichen ermitteln. Die restlichen Buchstaben ergeben sich aus dem Sinnzusammenhang.
Polyalphabetische Verschlüsselung
One-Time-Pad
Werden bei der Verschlüsselung die Buchstaben des Klartextes nicht immer durch denselben Buchstaben ersetzt, also beispielsweise A nicht immer durch C, sondern mal durch Z, mal durch E, mal durch B usw., so ist eine statistische Analyse nach obigem Muster nicht möglich. Eine solche Verschlüsselung, bei der die Chiffrierscheibe bei jedem Textzeichen neu eingestellt wird, bezeichnet man als polyalphabetische Verschlüsselung. Der Schlüssel ist die Folge der Buchstaben, auf die die Chiffrierscheibe eingestellt wird. Der Geheimtext ergibt sich durch Addition von Klartext und Schlüssel.
Ist der Schlüssel eine gleichverteilte Zufallsfolge von Buchstaben, so ist dieses Verschlüsselungsverfahren sogar absolut sicher. Dies liegt daran, dass es genausoviele mögliche Schlüssel wie mögliche Klartexte gibt, jeder Schlüssel gleichwahrscheinlich ist und somit auch jeder aus dem Geheimtext rekonstruierte Klartext gleichwahrscheinlich ist. Niemand kann sagen, ob der Schlüssel TXEDUBNHW oder YKREPHYPI war. Im einen Falle wird der Geheimtext TYIQXARPP zu ABENDZEIT entschlüsselt, im anderen Fall zu VORMITTAG.
Die Verschlüsselung durch Addition einer Zufallsfolge heißt Vernam-Chiffre oder One-Time-Pad.
Warum beschäftigt man sich überhaupt noch mit anderen Chiffrierverfahren, wenn doch ein absolut sicheres Verfahren bekannt ist? Der Nachteil des One-Time-Pad ist, dass der Schlüssel genauso lang wie der Klartext sein muss. Ferner muss der Schlüssel eine echte Zufallsfolge sein, und jeder Schlüssel darf auch nur ein einziges Mal verwendet werden, denn sonst wäre eine known-plaintext-attack möglich. Daher ist das Verfahren für die Praxis im Allgemeinen nicht geeignet.
Um dieses Problem zu umgehen, wird in einer ganzen Reihe von Verfahren versucht, mit kurzen Schlüsseln auszukommen, aus denen auf systematische Weise längere Schlüssel gewonnen werden. Dies geht allerdings auf Kosten der Sicherheit der Verfahren.
Vigenère-Chiffre
Eine Methode ist, einen periodischen Schlüssel zu verwenden, der durch fortgesetzte Aneinanderreihung eines kurzen Wortes entsteht, z.B. des Wortes ZEBRA. (Im obigen Übungsbeispiel lassen sich auch Wörter als Schlüssel eingeben). Diese Art der Verschlüsselung wird Vigenère-Chiffre genannt.
Auch bei diesem Verfahren wird z.B. das E mal auf F und mal auf I abgebildet, sodass eine einfache statistische Analyse nicht zum Ziel führt.
Dennoch ist bei periodischen Schlüsseln eine statistische Kryptanalyse möglich; bei einem Schlüssel der Länge 2 beispielsweise müssen 2 Statistiken erhoben werden – eine für die ungeraden und eine für die geraden Positionen des Geheimtextes, denn diese jeweils für sich sind ja monoalphabetisch verschlüsselt. Die Länge des Schlüssels wird durch Ausprobieren ermittelt.
Aus diesem Beispiel wird deutlich, dass ein "kryptisch" aussehender Geheimtext noch lange keine Gewähr dafür bietet, dass er nicht womöglich sogar relativ leicht zu entziffern ist. Auch wenn zur Verschlüsselung anstelle einfacher Verschiebungen beliebige Permutationen verwendet werden, ist die Kryptanalyse nicht wesentlich schwieriger.
Produkt-Chiffre
Die Periode des Schlüssels lässt sich verlängern, indem der Schlüssel in Teilschlüssel der Länge 2, 3, 5, 7, 11, ... zerlegt wird und der Klartext nacheinander mit diesen Teilschlüsseln verschlüsselt wird. Dies ist gleichbedeutend damit, dass aus den Teilschlüsseln zunächst ein Produktschlüssel gewonnen wird, mit dem dann der Klartext verschlüsselt wird. Die Periode des Produktschlüssels ist das Produkt der Teilschlüssellängen, die Schlüssellänge selbst ist aber nur gleich der Summe der Teilschlüssellängen. Bereits mit einem Schlüssel der Länge 77 = 2 + 3 + 5 + 7 + 11 + 13 + 17 + 19 lässt sich ein Produktschlüssel der Periode 107 erzeugen.
Beispiel: Der Schlüssel sei WOISTREVAL, Teilschlüssel sind WO, IST und REVAL.
Der Produktschlüssel hat die Periode 30; er errechnet sich wie folgt:
Autokey-Verfahren
Die Idee beim Autokey-Verfahren ist, einen kurzen Schlüssel durch den Klartext selbst zu verlängern.
Beispiel: Der Schlüssel sei ARGO.
Es ist klar, dass dieses Verfahren gegenüber einer known-plaintext-attack extrem unsicher ist. Aber auch durch statistische Analyse des Geheimtextes lässt sich der Klartext rekonstruieren. Der am häufigsten vorkommende Buchstabe im Geheimtext (im obigen Beispiel das I) entspricht an den meisten Positionen der Kombination E / E. Ist die Länge s des Schlüssels bekannt, so lässt sich ausgehend von diesen Positionen jedes s-te Klartextzeichen entschlüsseln (im Beispiel E_N_E_E_M_E_T).
Summen-Verfahren
Eine Modifikation des Autokey-Verfahrens besteht darin, jeden Klartextbuchstaben durch die Summe der s vorhergehenden Buchstaben und des Buchstabens selber zu verschlüsseln. Dadurch sollen die unterschiedlichen Buchstabenhäufigkeiten über einen Bereich der Länge s+1 gemittelt werden, sodass eine statistische Analyse nichts ergibt. Die s vorhergehenden Buchstaben des ersten Klartextbuchstabens werden wiederum durch einen Schlüssel der Länge s gebildet.
Beispiel: Der Schlüssel sei KEY.
Anhand des Schemas wird deutlich, dass jeweils zwei aufeinanderfolgende Buchstaben des Geheimtextes c durch Summation fast derselben Buchstaben des Klartextes m gebildet werden – nur ein Buchstabe ist jeweils anders. Es ist ci+1 = ci – mi-s + mi+1. Jedes Geheimtextzeichen hängt also in Wirklichkeit nur von zwei Klartextzeichen ab. Somit ist wiederum eine statistische Analyse wie beim einfachen Autokey-Verfahren möglich: Ist ci+1 = ci, so ist mi-s = mi+1. Die Wahrscheinlichkeit dafür, dass zwei bestimmte Klartextbuchstaben gleich sind, ist am höchsten, wenn diese gleich E sind. Wird die Länge des Schlüssels richtig erraten, so lässt sich im obigen Beispiel aufgrund der Geheimtextzeichen FF und RR der Klartext E_N_E_E_M_E_T rekonstruieren.
Enigma
Wenn die Periode des Schlüssels sehr lang wird, ist eine Entzifferung schwierig oder sogar unmöglich. Das Problem liegt jedoch darin, dass sehr lange Schlüssel in der Praxis schwer zu handhaben sind. Als Lösung wird versucht, einen langen Schlüssel aus einem kurzen Schlüssel zu erzeugen, aber nicht durch bloße Aneinanderreihung des kurzen Schlüssels, sondern auf kompliziertere Art und Weise.
In der im Zweiten Weltkrieg verwendeten deutschen Verschlüsselungsmaschine Enigma befinden sich drei Rotoren, die sich ähnlich wie ein Kilometerzähler bei jedem Buchstaben weiterdrehen. In jedem Rotor ist eine Permutation des Alphabets fest verdrahtet. Die Permutationen aller drei Rotoren sind hintereinandergeschaltet. Auf diese Weise entsteht eine sehr große Zahl unterschiedlicher Permutationen, und jedes Symbol des Klartextes wird mit einer anderen Permutation verschlüsselt. Als Parameter dieses Verschlüsselungsverfahrens war lediglich die Anfangsstellung der Rotoren zu übermitteln, dieser Parameter stellte den täglich wechselnden kurzen Schlüssel dar.
Lediglich aus Kenntnis des Geheimtextes ist dieser Code nicht zu entschlüsseln. Das Problem ist jedoch, dass nicht nur der Schlüssel, sondern insbesondere die Rotoren geheimzuhalten sind, die die Systematik der Erzeugung des langen Schlüssels enthalten. Außerdem ist dieses Verschlüsselungsverfahren nicht gegenüber einer known-plaintext-attack sicher. Tatsächlich wurde die Enigma sowohl von den Polen als auch von den Engländern recht bald geknackt.
Pseudozufallsfolgen
Die zuletzt erwähnten Verfahren kranken alle daran, dass aus einem relativ kurzen Schlüssel in systematischer Weise ein langer Schlüssel generiert wird. Gelingt es, die Systematik der Schlüsselerzeugung zu durchschauen, so ist der lange Schlüssel nicht sicherer als der kurze Schlüssel.
Nur wenn der lange Schlüssel keinerlei Systematik unterliegt, wie dies beim One-Time-Pad der Fall ist, ist das Verfahren absolut sicher. Wie bereits erwähnt, ist der Nachteil dieses Verfahrens, dass ein sehr langer Schlüssel notwendig ist. Naheliegend ist daher die Idee, anstelle der beim One-Time-Pad verwendeten Zufallsfolge eine Pseudozufallsfolge zu verwenden. Sender und Empfänger verwenden denselben Zufallszahlengenerator. Sie brauchen nur den Startwert des Zufallszahlengenerators zu vereinbaren und können somit beide dieselbe Zufallsfolge erzeugen. Das Problem des Austauschs eines langen Schlüssels entfällt also.
Allerdings enthält eine Pseudozufallsfolge, auch wenn sie zufällig aussieht, eine sehr starke Systematik, nämlich die des Zufallszahlengenerators. Schon wenige Zeichen des Klartextes zusammen mit dem entsprechenden Geheimtext reichen möglicherweise aus, um diese Systematik zu durchschauen und alle weiteren und alle vorhergehenden Zufallszeichen zu erzeugen. Diese scheinbar geringfügige Abwandlung eines perfekten Verschlüsselungsverfahrens (Pseudozufallszahlen anstelle echter Zufallszahlen) führt also zu einem extrem unsicheren Verfahren (siehe Erzeugung von Zufallsbits).
Literatur
[Beu 97] A. Beutelspacher: Geheimsprachen. C.H. Beck (1997)
[Wel 88] D. Welsh: Codes and Cryptography. Oxford University Press (1988)
[Lan 23] H.W. Lang: Kryptografie für Dummies. 2. Auflage, Wiley (2023)
Weiter mit: [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 12.02.2001 Updated: 19.04.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden
