Berechnungsverfahren
Quadratisches Sieb
Die Sicherheit des RSA-Verschlüsselungsverfahrens beruht darauf, dass es schwer ist, eine große ganze Zahl n zu faktorisieren, d.h. in ihre Primfaktoren zu zerlegen. Das naheliegende Faktorisierungsverfahren, nämlich Probedivision von n durch die Primzahlen 2, 3, 5, 7, 11, usw., ist hoffnungslos zu langsam, denn es gibt zu viele Primzahlen.
Als Beispiel für ein schnelleres, wenn auch für sehr große Zahlen n immer noch praktisch undurchführbares Faktorisierungsverfahren wird im Folgenden das Quadratische Sieb (engl.: quadratic sieve) dargestellt [Pom 96].
Idee
Wenn für zwei ganze Zahlen x und y gilt
x2 ≡ y2 (mod n),
so gilt nach Definition von ≡
n | x2 – y2
und damit nach der binomischen Formel
n | (x+y)·(x- y).
Sofern n nicht bereits einen dieser beiden Faktoren teilt, sind mit
ggt(n, x+y) und ggt(n, x-y)
zwei Faktoren von n gefunden.
Die Bedingung, dass n weder x+y noch x-y teilt, lässt sich nach Definition von ≡ formulieren als
x  ±y (mod n)
±y (mod n)
Ziel ist es also, zwei Zahlen x, y ∈ ℤ zu finden, für die gilt
x2 ≡ y2 (mod n) und
x  ±y (mod n).
±y (mod n).
Als Beispiel sei die Zahl n = 2041 zu faktorisieren. Wir bilden die Folge der auf 2041 folgenden Quadratzahlen xi2 und die Folge der Differenzen xi2 – n.
| xi2 | 462 | 472 | 482 | 492 | 502 | 512 | ... |
|---|---|---|---|---|---|---|---|
| xi2 – n | 75 | 168 | 263 | 360 | 459 | 560 | ... |
Ist eine der Zahlen xi2 – n eine Quadratzahl y2, so gilt
| xi2 – n | = | y2 | |
| ⇒ | xi2 | ≡ | y2 (mod n) |
In diesem Beispiel wird erst bei 852 – n = 5184 = 722 eine Quadratzahl gefunden. Ist n sehr groß, so dauert es möglicherweise sehr lange, bis unter den xi2 – n eine Quadratzahl gefunden wird.
Produkt von Differenzen
Im obigen Beispiel ist keine einzelne der aufgeführten Zahlen xi2 – n eine Quadratzahl. Aber auch wenn ein Produkt mehrerer Zahlen xij2 – n eine Quadratzahl ergibt, etwa y2, so gilt
y2 ≡ (xi12 – n) · ... · (xik2 – n) ≡ xi12 · ... · xik2 ≡ (xi1 · ... · xik)2 ≡ x2 (mod n)
Sofern hierbei
x  ±y (mod n)
±y (mod n)
gilt, ist eine Zerlegung von n in Faktoren gefunden.
Im Beispiel ist das Produkt folgender xij2 – n eine Quadratzahl:
75 · 168 · 360 · 560 = 504002 = y2
Modulo n ist diese Quadratzahl y2 kongruent zum Produkt x2 der entsprechenden xij2 :
462 · 472 · 492 · 512 = (46 · 47 · 49 · 51)2 = 54028382 = x2
Es stellt sich heraus, dass
5402838 ≡ 311 (mod 2041) und
50400 ≡ 1416 (mod 2041) sowie
311 ±1416 (mod 2041)
±1416 (mod 2041)
gilt. Somit ergibt
ggt(1416-311, 2041) = 13
einen Faktor von n = 2041.
Sieb
Das Problem ist: Wie findet man eine geeignete Auswahl von Zahlen xij2 – n, deren Produkt eine Quadratzahl y2 ist?
In der Primfaktorzerlegung einer Quadratzahl muss jeder Primfaktor einen geraden Exponenten haben. Daher wird jede der Zahlen xi2 – n zunächst in ihre Primfaktoren zerlegt, und es werden dann diejenigen Zahlen ausgewählt, die zu einem Produkt von Primzahlpotenzen mit geraden Exponenten kombiniert werden können.
Im Beispiel ist etwa
| 75 | = 3 · 52 | |
| 168 | = 23 · 3 · 7 | |
| 360 | = 23 · 32 · 5 | |
| 560 | = 24 · 5 · 7 |
Im Produkt aller vier Zahlen hat jeder Primfaktor einen geraden Exponenten:
75 · 168 · 360 · 560 = 210 · 34 · 54 · 72 = y2
Technisch lässt sich die Suche wie folgt durchführen. Zunächst wird eine Faktorbasis festgelegt. Dies sind diejenigen Primfaktoren, die bei den möglichen Kombinationen eine Rolle spielen sollen; zweckmäßigerweise werden hierzu alle Primzahlen unterhalb einer festen Grenze B genommen. Nehmen wir für das Beispiel B = 10, so ist die Faktorbasis
a = 2, 3, 5, 7
In einer ähnlichen Weise wie beim Sieb des Eratosthenes1) wird nun mit jedem Element aj der Faktorbasis die Folge der xi2 – n durchlaufen (siehe Bild 1). Dabei wird, so oft es ganzzahlig geht, durch aj geteilt.
Der Siebvorgang wird wie folgt durchgeführt. Ist unter den ersten p Zahlen xi2 – n eine durch p teilbare Zahl, so sind auch alle in p-Schritten folgenden Zahlen durch p teilbar; ist xi2 – n nicht durch p teilbar, so sind auch alle in p-Schritten folgenden Zahlen nicht durch p teilbar. Denn es gilt für alle k ∈ ℤ
xi2 – n ≡ (xi+k·p)2 – n (mod p).
Unter den ersten p Zahlen xi2 – n können höchstens zwei durch p teilbare Zahlen sein, denn xi2 – n ist ein Polynom vom Grad 2; es hat daher im Körper ℤp höchstens zwei Nullstellen, und diese treten bei den ersten p aufeinander folgenden Werten xi irgendwo auf.
Im Beispiel sind etwa von den ersten 5 Zahlen die erste (75) und die vierte (360) durch 5 teilbar. Daher sind auch die 6., 11., 16. usw. sowie die 9., 14., 19. usw. Zahl durch 5 teilbar.
Um also r Folgenelemente xi2 – n durch ein Element p der Faktorbasis zu dividieren, sind maximal 2r / p Schritte erforderlich.
| 75 | 168 | 263 | 360 | 459 | 560 | |
| 2 | 20 | 23 | 20 | 23 | 20 | 24 |
| 75 | 21 | 263 | 45 | 459 | 35 | |
| 3 | 31 | 31 | 30 | 32 | 33 | 30 |
| 25 | 7 | 263 | 5 | 17 | 35 | |
| 5 | 52 | 50 | 50 | 51 | 50 | 51 |
| 1 | 7 | 263 | 1 | 17 | 7 | |
| 7 | 70 | 71 | 70 | 70 | 70 | 71 |
| 1 | 1 | 263 | 1 | 17 | 1 | |
Bild 1: Schema des Siebvorgangs
Diejenigen Elemente xi2 – n, die zum Schluss zu 1 geworden sind, lassen sich durch die Faktorbasis mit einem geeigneten Exponentenvektor darstellen. Die Zahl 75 ergibt beispielsweise den Exponentenvektor
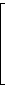 |
| 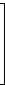 |
denn es ist 75 = 20 · 31 · 52 · 70.
Da es nicht auf die tatsächlichen Exponenten ankommt, sondern nur darauf, ob diese gerade oder ungerade sind, lässt sich mit den modulo 2 reduzierten Exponentenvektoren rechnen. Diese sind Elemente eines Vektorraums über 𝔹 = {0, 1}.
Auswahl von Exponentenvektoren
Unter diesen Vektoren wird eine Menge von linear abhängigen Vektoren gesucht, also eine Auswahl von gewissen Vektoren, deren Summe den Nullvektor ergibt (modulo 2 gerechnet). Dies entspricht der Lösung eines linearen Gleichungssystems; im Beispiel ist dieses
| λ0· |
| + λ1· |
| + λ2· |
| + λ3· |
| = |
|
Dieser Schritt verursacht den größten Rechenaufwand.
Für das Beispiel ergibt sich λ0 = λ1 = λ2 =λ3 = 1; es bilden also alle vier aufgeführten modulo 2 reduzierten Exponentenvektoren eine linear abhängige Menge. Wie gesehen, ergibt das zugehörige Produkt 75 · 168 · 360 · 560 eine Quadratzahl.
Die Zahlen xi2 – n lassen sich auch für x2 < n verwenden; dann wird xi2 – n negativ. In die Primfaktorzerlegung muss dann auch die Einheit -1 einbezogen werden, und die -1 muss in die Faktorbasis mit aufgenommen werden.
Literatur
[Bu 00] J.A. Buchmann: Introduction to Cryptography. Springer (2000)
[Pom 96] C. Pomerance: A Tale of Two Sieves. Notices of the AMS, 43, 12, 1473-1485 (1996)
[Lan 18] H.W. Lang: Kryptografie für Dummies. Wiley (2018)
1) Verfahren zur Berechnung aller Primzahlen kleiner als k: In der Liste der Zahlen von 2 bis k werden alle echten Vielfachen von 2 gestrichen, dann alle echten Vielfachen von 3, dann von 4, dann von 5 usw. Die Zahlen, die übrig bleiben, sind die Primzahlen.
Weiter mit: [up]
H.W. Lang mail@hwlang.de Impressum Datenschutz
Created: 05.02.2005 Updated: 17.02.2023
Diese Webseiten sind während meiner Lehrtätigkeit an der Hochschule Flensburg entstanden
